布隆过滤器与布谷鸟过滤器原理详解：大数据去重与缓存穿透实战指南

在数据洪流时代，如何在海量信息中快速甄别一个元素是否存在，是许多系统面临的基础挑战。直接查询完整的集合或数据库不仅效率低下，在高并发场景下还可能成为性能瓶颈。布隆过滤器（Bloom Filter）与布谷鸟过滤器（Cuckoo Filter）便是为解决此类问题而生的两种高效概率型数据结构。本文将深入剖析两者的核心原理、优缺点及适用场景，帮助你在实际开发中做出合适的选择。

一、布隆过滤器（Bloom Filter）

1.1 核心概念

布隆过滤器由 Burton Howard Bloom 于1970年提出，是一种空间效率极高的数据结构。其核心是一个很长的二进制位数组和一系列相互独立的哈希函数。它的主要作用是判断一个元素 “可能存在” 或 “一定不存在” 于某个集合中。

你可以将其理解为一个“简版”的哈希集合（Hash Set）。但与普通集合不同，它并不存储元素本身，而是为每个元素通过多个哈希函数在位数组上打上几个标记位。查询时，只需检查这些标记位是否都被置为“1”。

1.2 工作原理

布隆过滤器的工作原理分为初始化和操作两个阶段。

1. 初始化 初始化需要确定两个关键参数：位数组大小 m 和哈希函数个数 k。这两个参数直接决定了过滤器的误判率（False Positive Rate）。误判是指一个本不存在的元素，其对应的所有 k 个位恰好都被其他元素置为1，从而被误认为存在。以下是参数选择的数学推导摘要：

假设哈希函数等概率地设置位数组中的任意一位。插入 n 个元素后，某一位仍然为0的概率是： (1 - 1/m)^{kn}

因此，该位为1的概率是： 1 - (1 - 1/m)^{kn}

那么，在查询时，一个不存在的元素被误判为存在的概率（即所有 k 个指定位都为1）约为： p ≈ (1 - e^{-kn/m})^k

为了使误判率最低，最优的哈希函数数量 k 为： k = (m/n) * ln2

而对于给定的预期元素数量 n 和可接受的误判率 p，最优的位数组大小 m 为： m = - (n * ln p) / (ln 2)^2

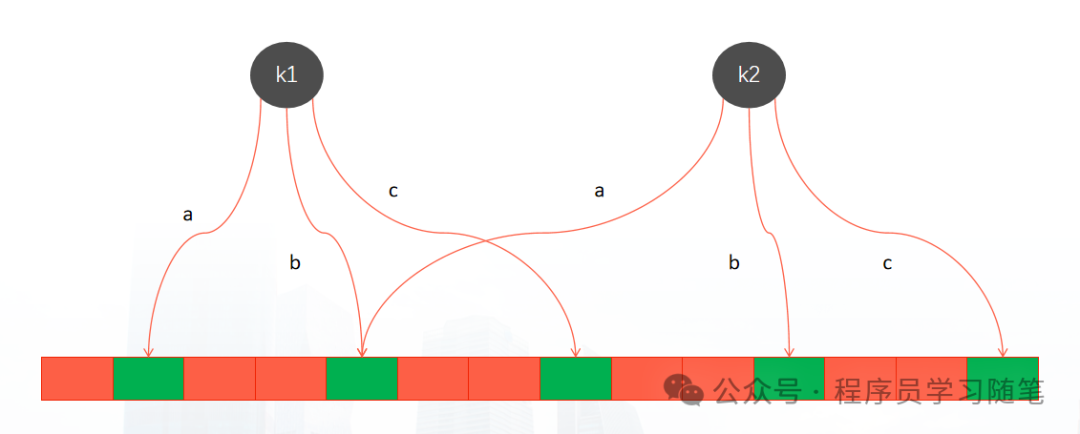
2. 插入与查询

• 插入元素：将待插入元素输入 k 个哈希函数，得到 k 个位置，并将位数组中这些位置的值置为1。
• 查询元素：同样计算该元素的 k 个哈希位置。如果这些位置全部为1，则认为元素可能存在（需进一步确认）；如果任何一个位置为0，则元素一定不存在。

1.3 应用场景与优缺点

应用场景：适用于对查询效率要求极高、且能容忍一定误判率的场景。

• 缓存穿透防护：在查询数据库/缓存前，先检查布隆过滤器。若过滤器说“不存在”，则直接返回，避免对底层存储的无效冲击。
• LevelDB/RocksDB：快速判断某个键是否可能存在于某个SSTable文件中，避免不必要的磁盘IO。
• 网页爬虫去重：判断一个URL是否已被爬取过。

优点：

1. 空间效率极高：不存储元素本身，只占用若干比特位。
2. 查询时间极快：仅需进行常数次（k次）哈希计算和位操作，时间复杂度为O(k)。

缺点：

1. 存在误判率：无法做到100%准确。
2. 不支持删除：由于多个元素可能共享同一个位，删除一个元素（将其对应位置0）可能会影响其他元素的判断结果。

二、布谷鸟过滤器（Cuckoo Filter）

2.1 核心概念

布谷鸟过滤器是对布隆过滤器的改进，它同样用于成员查询，但在设计上支持了删除操作，并且通常具有更高的空间利用率。其灵感来源于布谷鸟的“鸠占鹊巢”行为。它将元素的一个小指纹（fingerprint）存储在一个哈希表桶中，每个桶可以存放多个指纹。

2.2 工作原理

1. 布谷鸟哈希（Cuckoo Hashing） 要理解布谷鸟过滤器，先需了解其基础的布谷鸟哈希。它使用两个哈希函数 h1(x) 和 h2(x) 为元素 x 提供两个候选桶位置。

• 插入：尝试放入 h1(x) 或 h2(x) 指向的桶。若两个桶均满，则随机“踢出”（evict）其中一个桶内的一个已有元素，将新元素放入，再为被踢出的元素寻找其另一个候选桶位置（即“鸠占鹊巢”）。
• 为防止无限循环，会设置一个最大踢出次数，超过则判定哈希表已满，需要进行扩容。

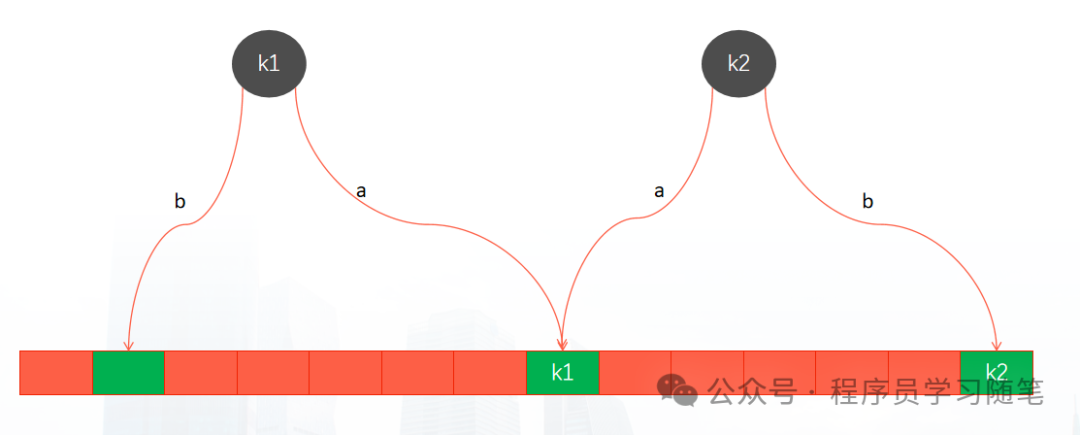
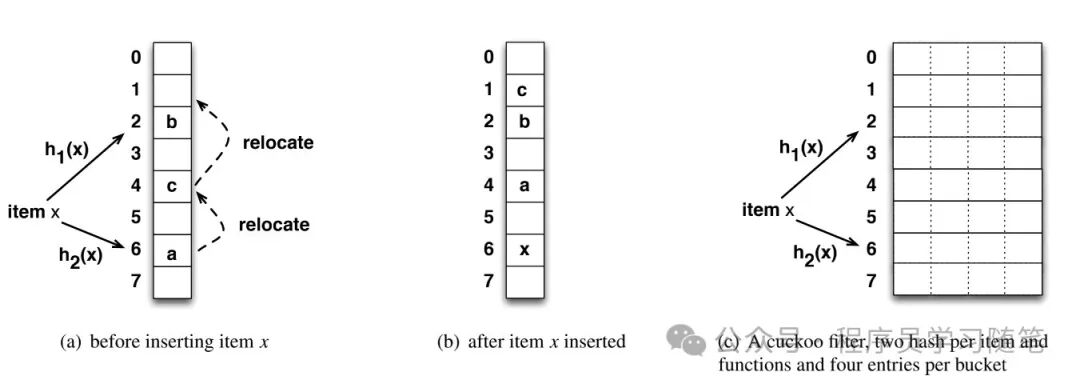
2. 布谷鸟过滤器设计 布谷鸟过滤器在布谷鸟哈希的基础上，存储的是元素的指纹而非元素本身，并利用指纹的巧妙计算来定位桶。

• 数据结构：一个由多个桶（bucket）组成的数组，每个桶可容纳 b 个指纹（例如，每个指纹 f 为若干比特）。

  type bucket [4]byte  // 示例：一个桶可容纳4个指纹（每个指纹8比特）
  type cuckoo_filter struct {
      buckets [size]bucket
      count   int         // 当前元素数量
      maxKicks int       // 最大踢出次数
  }

• 哈希计算：

  1. 计算元素 x 的指纹：fp = fingerprint(x)
  2. 计算第一个候选桶索引：i1 = hash(x)
  3. 计算第二个候选桶索引：i2 = i1 ^ hash(fp) （^ 表示异或操作） 这种设计的精妙之处在于对偶性：i1 = i2 ^ hash(fp)。这意味着，只要知道当前位置 i 和指纹 fp，就能立刻计算出另一个候选桶的位置，而无需知道元素 x 本身。

• 操作：

  • 插入：尝试将指纹 fp 放入桶 i1 或 i2。若均满，则随机踢出某个指纹，放入 fp，然后为被踢出的指纹计算其另一个桶位置（使用上述对偶性公式），重复此过程直到成功或达到 maxKicks。
  • 查询：计算 x 的指纹 fp 和两个候选桶 i1、i2。检查这两个桶中是否存在指纹 fp。存在则返回 true，否则返回 false。
  • 删除：查询到元素存在的桶，并从该桶中移除对应的指纹即可。这是布谷鸟过滤器相比布隆过滤器的关键优势。

2.3 应用场景与优缺点

应用场景：适用于需要高效存在性判断且必须支持删除操作的场景。

• 去重系统：需要支持数据过期或撤销的场景。
• 数据库与存储引擎：作为索引的辅助结构。
• 网络设备与中间件：需要动态更新规则集的场景。

优点：

1. 支持动态删除：可以安全地移除已添加的元素。
2. 更高的查询性能与空间利用率：在相同误判率下，通常比布隆过滤器占用更小空间，且查询通常只需访问两个确定的内存位置，对CPU缓存更友好。
3. 较低的误判率：在精心设计参数下，可以实现比布隆过滤器更低的误判率。

缺点：

1. 插入性能不稳定：在负载较高时，可能因频繁的“踢出”操作导致插入延迟增加。
2. 对重复元素敏感：插入大量重复元素会迅速填满桶，影响性能。通常需要额外机制处理重复项。
3. 负载因子有上限：当存储的元素数量超过一定阈值（如桶数组容量的95%）后，插入失败率会急剧上升，必须扩容。

总结与选择建议

特性	布隆过滤器	布谷鸟过滤器
空间效率	高	通常更高
查询速度	O(k) 次内存访问	O(1) 次内存访问（通常只需查2个桶）
删除支持	不支持	支持
插入性能	稳定，O(k)	不稳定，高负载时可能退化
误判率	由 m, n, k 决定	由桶大小、指纹长度决定，设计得当可更低
实现复杂度	简单	相对复杂

如何选择？

• 选择布隆过滤器：如果你的场景只增不删，对实现简单性要求高，且可以接受固定的误判率。它是防止缓存穿透的经典选择。
• 选择布谷鸟过滤器：如果你的场景需要支持元素删除，对空间效率和查询性能有极致要求，并且愿意接受相对复杂的实现和插入时可能的不稳定性。

两者都是解决海量数据存在性查询的利器，理解其内在原理和权衡，方能使其在分布式系统、数据库、网络等领域的实战中发挥最大价值。