为了方便射频采样接收机设计,TI 提供了三个实用工具。首先是频率规划工具,它能快速分析并帮助工程师找到适合特定输入频段的 ADC 采样率,或者在固定采样率下确定最合适的信号中心频率。
其次是模拟滤波器设计工具,它可以根据 ADC 采样率、输入频率范围、系统 SFDR 要求以及 ADC 自身的谐波性能,来估算外部射频滤波器所需的性能指标。设计师可以借此快速评估射频采样设计的可行性。
第三个是抽取滤波器杂散计算器。在调试阶段,如果只观察经过抽取滤波后的输出频谱,往往难以判断杂散的来源。这个工具能够清晰地展示特定 ADC 杂散经过复杂的数字抽取滤波后,最终会落在输出频谱的什么位置。
频率规划工具详解
该工具的核心功能是自动计算带内信号在频域可能产生的无用杂散位置,用户可以通过调节 ADC 采样率、输入信号的中心频率和带宽来进行分析。
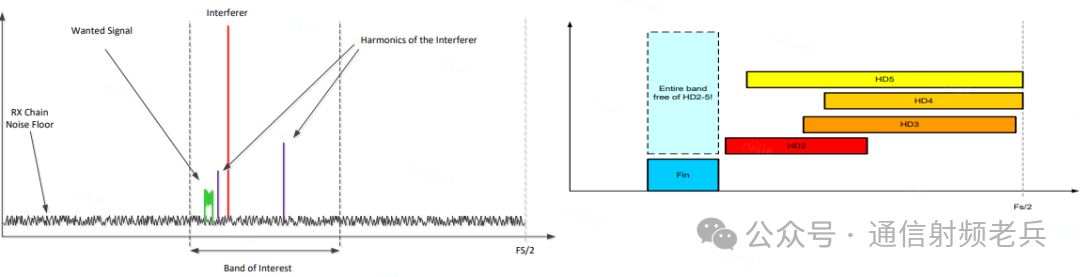
使用前需要输入几个关键参数:ADC采样率、交织倍数(支持非交织、2倍交织和4倍交织)、输入信号的中心频率和带宽。随后,工具会自动计算哪些杂散会与有用频段重叠,并以图形方式展示接收频段(蓝色部分)和所有无用杂散。当调节交织倍数时,工具会自动增减与交织相关的杂散。
示例:ADC时钟频率为2.9Gsps,采用2倍交织,输入信号中心频率为2.05GHz,带宽100MHz。工具分析显示没有主要杂散与有用频段重叠,从图形上也能直观看出频谱很干净。
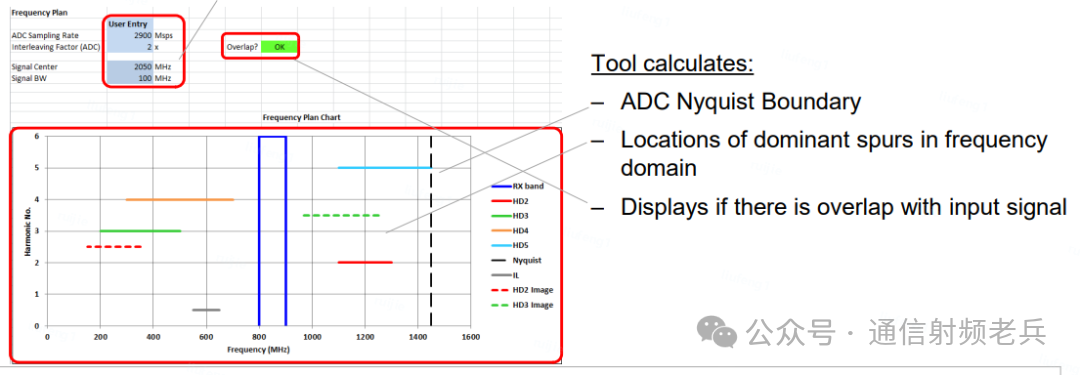
放大图形可以看到以下内容:蓝色的有用信号频段、黑色的奈奎斯特区边界、需要避开的2到5次低阶谐波杂散(其中2次和3次最严重)、随交织倍数变化的交织杂散,以及交织ADC特有的2次和3次谐波镜像。
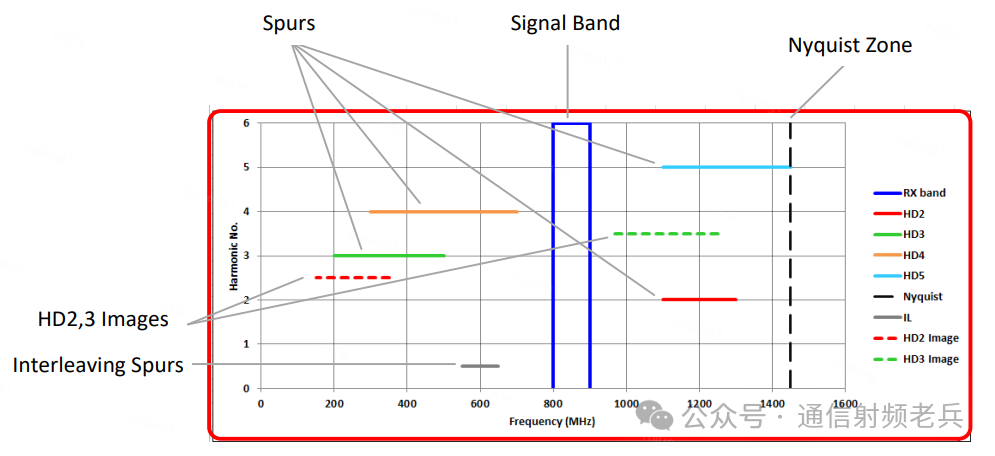
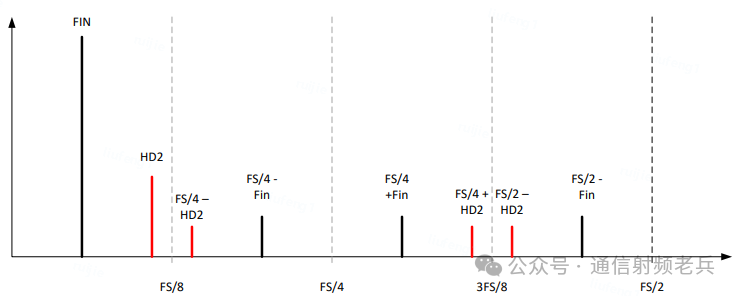
什么是谐波镜像? 在交织ADC架构中,2到5次低阶谐波会与内部交织时钟频率混频,产生一种被称为“低阶谐波镜像”的杂散。它们的幅度虽然比主谐波低得多,但通常高于噪声基底,因此能够被检测到。例如,在4倍交织ADC中,输入信号的2次谐波会与 fs/2、fs/4 等交织时钟混频,产生 fs/2-HD2、fs/4±HD2 等镜像分量,图中以红色标示。
频率规划案例解析
首先看固定射频频段的情况,例如通信系统直接采样3G频段,或将X波段等高频信号下变频到L波段后再采样。
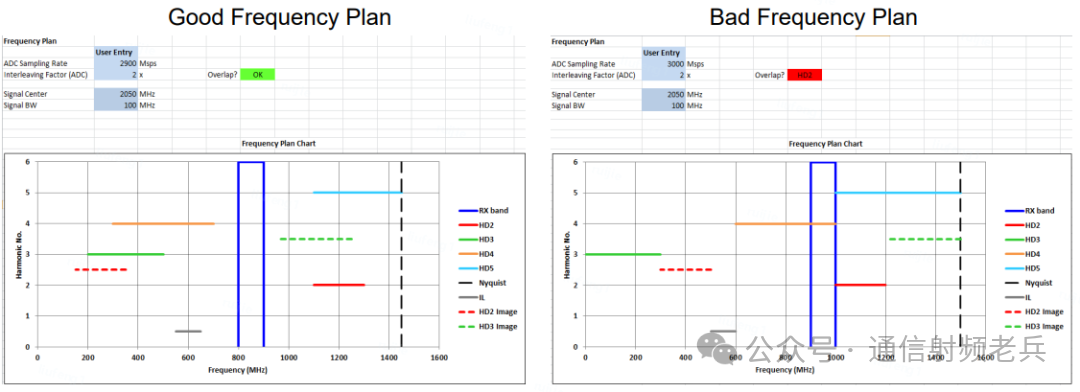
示例中的有用信号带宽为100MHz,中心频率2050MHz。当使用2.9Gsps时钟和2倍交织时,频谱干净,无杂散重叠(左图);但如果将时钟换成3Gsps,情况发生变化,2次、5次谐波有部分重叠,4次谐波则完全落在带内(右图)。
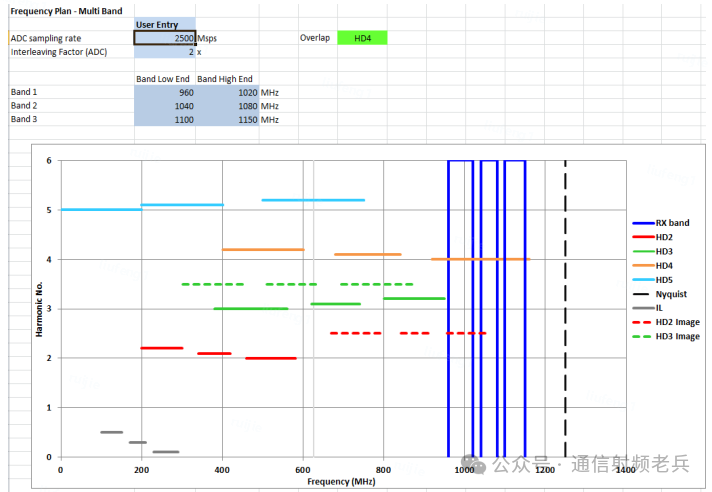
有些系统基于固定参考时钟,无法更改采样率。这种情况下,只能调整有用频段的中心频率。例如,固定ADC时钟为3Gsps,信号带宽200MHz:当中心频率为1950MHz时,2次、4次、5次谐波和3次谐波镜像均落在带内,性能很差;然而,将中心频率调整到1850MHz后,带内最严重的杂散变为3次谐波镜像和4次谐波,系统SFDR可提升10-15dB。这种对中心频率的精细调整,本质上是算法优化的一种体现,旨在寻找最佳的系统工作点。

进行频率规划有一个前提:有用信号带宽最好不超过ADC采样率的10%。因为2次谐波的带宽是基波信号的2倍,3次谐波是3倍,如果信号带宽过大,频谱会过于拥挤,导致规划变得困难。
现代接收机面临多频段接收等新挑战,即利用ADC的高采样率同时采样多个频段。因此,该工具也支持多频段规划,最多可输入3个接收频段,通常做法是固定各频段中心频率,然后调节ADC采样率来寻找合适的无杂散频谱。
工具预测与实际测试对比
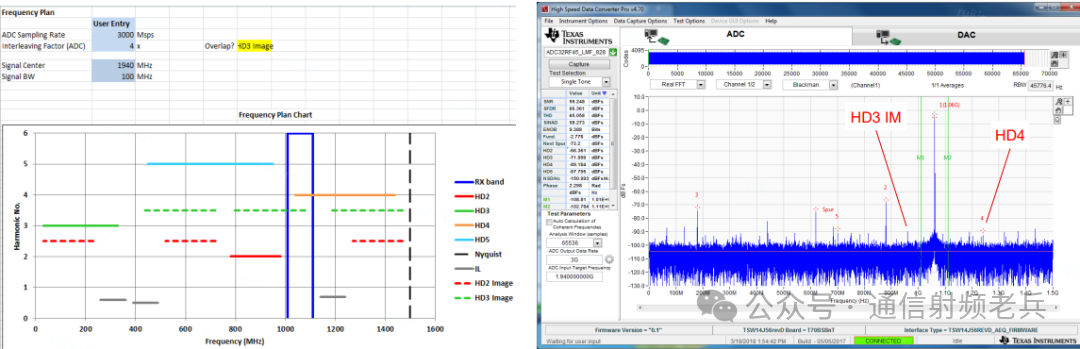
为了验证工具的准确性,我们使用某款射频采样ADC进行了测试。条件为:采样率3Gsps,输入信号中心频率1.94GHz,带宽100MHz。工具清晰显示了需要避开的2次、3次谐波、3个与频率相关的交织杂散,以及可能落入带内的3次谐波镜像和4次谐波。
右图是实际测试的FFT结果,绿色标记为频段边缘。当信号位于频段中心时,4次、3次谐波均落在带外,带内SFDR性能良好,与工具预测完全一致。
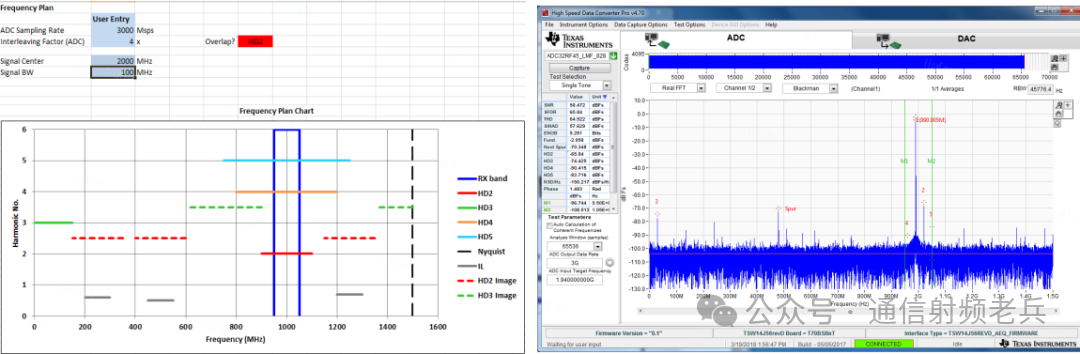
随后,保持其他参数不变,仅将信号中心频率从1.94GHz调整到2GHz。频率规划工具显示,此时2次、4次、5次谐波都将落入带内。实际测试的FFT图(输入信号2GHz)证实,这三个杂散确实出现在带内,导致带内SFDR显著下降。
外部射频模拟滤波器设计工具
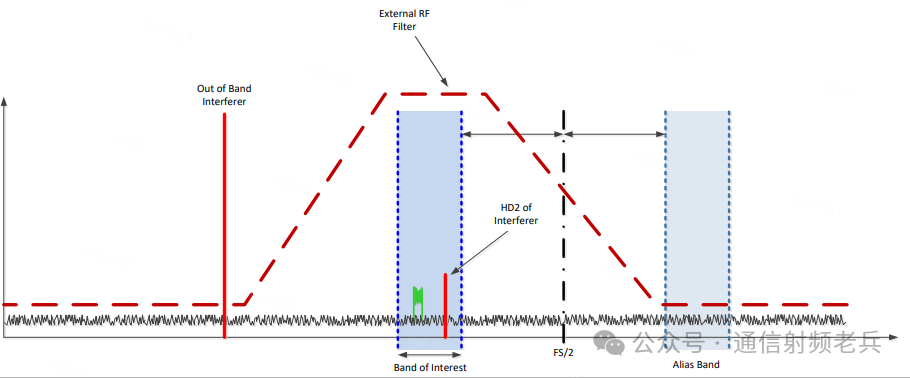
外部射频模拟滤波器的作用是保护ADC,免受无用带外信号的影响。这些带外信号会在ADC内部产生谐波杂散。滤波器既要滤除信号的镜像频段,也要滤除那些会产生带内谐波的带外干扰信号。
ADC采样率越高,奈奎斯特区越宽,镜像频段距离越远,对滤波器阶数和滚降率的要求就可能降低。然而,带外干扰在ADC内部产生的谐波可能折叠到带内,加上杂散在其他奈奎斯特区的折叠效应,计算所需的滤波衰减值变得非常复杂。这要求在前端与系统设计阶段就要进行周密的考量。
因此,TI 提供了一个简化计算器。它会在DC到4GHz范围内进行扫频,根据设定的系统SFDR目标,计算出不同频率下外部滤波器所需提供的衰减值。
使用方法:
- 设置系统参数(ADC采样率、输入信号频率范围)。
- 指定由带外干扰导致的带内SFDR上限(例如设为100dB)。
- 导入ADC的2次谐波等杂散的SFDR性能数据。
- 工具自动生成所需的滤波器衰减指标。
以2次谐波为例(其他杂散逻辑相同):假设ADC自身的2次谐波性能为65dB,而系统要求带内SFDR达到100dB,那么外部滤波器就需要在特定频点上提供额外的35dB阻带衰减。假设有用信号中心频率为1800MHz,那么中心在900MHz的干扰信号产生的2次谐波正好会落在1800MHz的有用频段上。
在示例中,信号带宽为100MHz。由于2次谐波的带宽是基波的2倍,因此滤波器只需要在中心为900MHz、宽度为50MHz的频段上提供至少35dB的衰减即可。实际设计中,衰减要求可以略微放宽,因为当干扰信号幅度降低后,ADC本身对低阶谐波的抑制性能(如SFDR)也会有所改善,3次及以上谐波的计算同理。
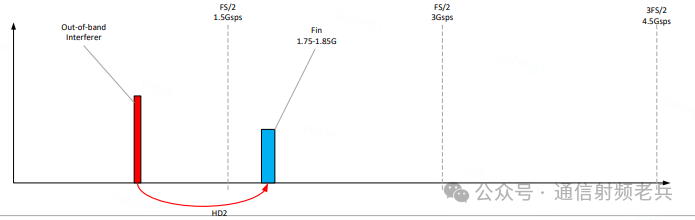
具体分析:输入信号位于1750到1850MHz(第二个奈奎斯特区),相邻的是第一和第三奈奎斯特区。
- 第一个奈奎斯特区的镜像频段是1150到1250MHz,因此需要在其一半频率(575到625MHz)的50MHz带宽上提供衰减。
- 第三个奈奎斯特区的镜像频段是4150到4250MHz,因此需要在2075到2125MHz频段上提供衰减。

实际操作演示:输入信号带宽100MHz,中心1800MHz,ADC采样率3Gsps,4倍交织。工具会标出奈奎斯特区边界,红色区域为接收频段。设置带外SFDR上限为100dB,并输入ADC的2次谐波性能为65dB等参数后,工具会生成一个表格,显示针对主要杂散所需的滤波衰减及其对应的频率位置,帮助判断滤波要求是否现实;同时还会绘制出从DC到4GHz的滤波衰减曲线,这直接构成了射频滤波器的初步设计指标。
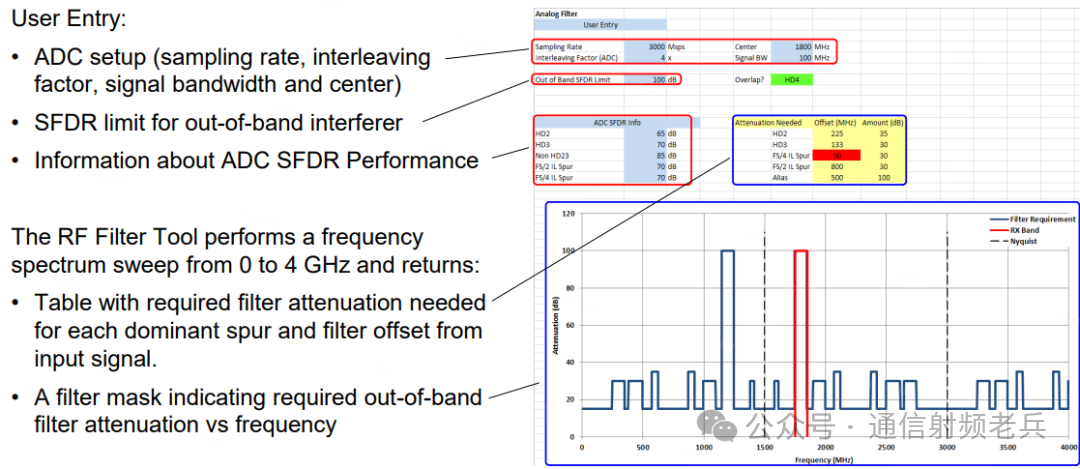
在示例的表格中:
- 高阶谐波(如5次以上)的衰减要求设为15dB,这意味着需要在全频段提供一定的基底衰减,以防止随机杂散混叠到带内影响100dB的SFDR目标。
- 12MHz处的信号镜像需要高达100dB的衰减,因为此处的干扰会直接混叠到有用信号上,必须强力抑制。
- 600MHz和900MHz处需要35dB衰减,这与我们之前手动计算的2次谐波衰减要求一致。

请注意:这只是一个初步评估工具,它没有考虑滤波器衰减导致的信号幅度变化(这实际上会改善ADC对低阶谐波的抑制性能)。
抽取滤波器杂散计算器
当使用复杂的数字抽取滤波器时,尤其是在电路板调试阶段,工程师很难直接判断输出频谱中某个杂散的来源。这个工具能够将ADC的各种本征杂散映射到经过抽取后的输出频谱上。
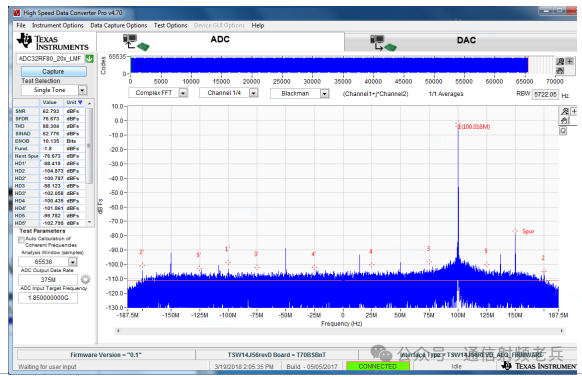
下图是某款射频采样ADC经过8倍复数抽取后的输出FFT频谱。可以看到ADC的本底噪声非常干净,但在150、50、15、-50、-150MHz等处出现了几个较大的杂散。TI的HSDC Pro软件在知晓抽取配置的情况下可以很好地映射ADC谐波,但如果使用MATLAB等其他工具进行分析,这个计算器就非常有用了,它能有效辅助运维与调试工作。
与其他工具类似,它也需要输入ADC采样率、交织倍数、输入频率(注意,此工具针对单频点信号分析,而非信号带宽)。在配置抽取滤波器时,需要输入复数抽取倍数和数控振荡器(NCO)的频率。
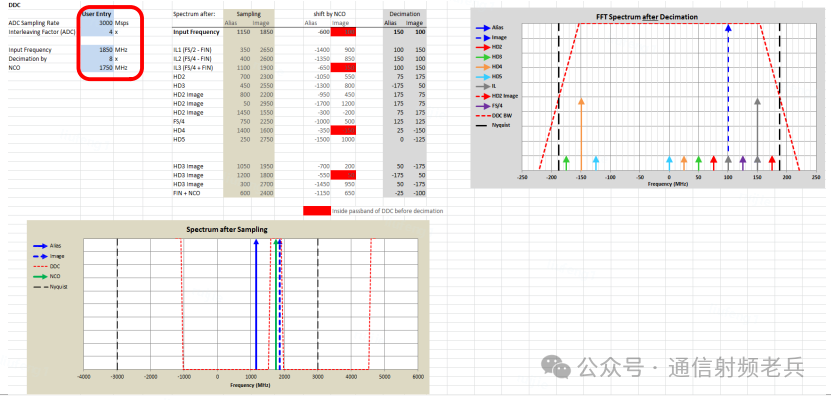
以下示例参数与实际测试条件一致:ADC采样率3Gsps,4倍交织,8倍复数抽取,输入频率1850MHz,NCO频率1750MHz。工具的计算分为三步:
第一步:计算采样后频谱(ADC端)
即信号经过ADC采样但未经过任何数字处理前的频谱。工具会计算出输入信号及其主要杂散(谐波、交织杂散)折叠到第一个奈奎斯特区后的位置,可称之为“混叠频率”。在进行复数抽取分析时,既要考虑正频率分量,也要考虑其对应的负镜像频率。
一种简单的理解方式是将负频率加上一个采样率 fs,相当于将其移到第二个奈奎斯特区内。表格中的“混叠”和“镜像”两列即按此方式处理。例如,1850MHz的输入信号,在第一奈奎斯特区混叠为1150MHz;其-1150MHz的负镜像,加上 1*fs (3000MHz) 后变为1850MHz,即落在第二奈奎斯特区。图中会标出奈奎斯特区边界、NCO频率以及抽取滤波器的响应。
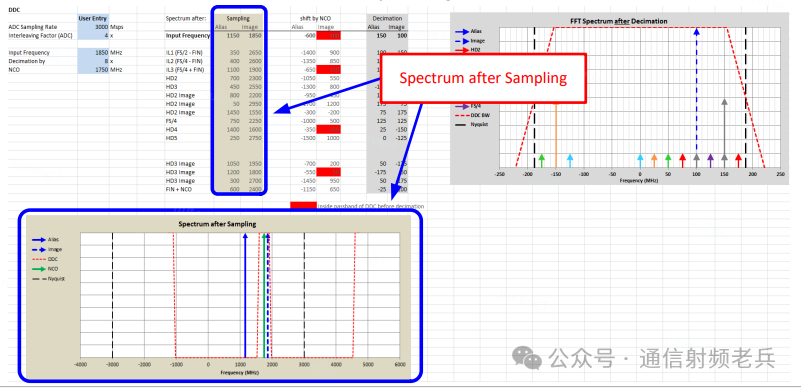
第二步:NCO混频
将第一步中得到的第一奈奎斯特区的正混叠频率,以及挪到第二奈奎斯特区的负镜像频率,分别与数字NCO的频率进行混频(相减)。例如,1150MHz的混叠信号减去1750MHz的NCO频率,得到-600MHz。
同样,1850MHz的信号镜像减去NCO频率后得到+100MHz。在此步骤中,如果NCO移频后的频率落在了抽取滤波器的通带内,表格中对应的频率数值会被标红,意味着这些频率分量将通过滤波器,不会被衰减。
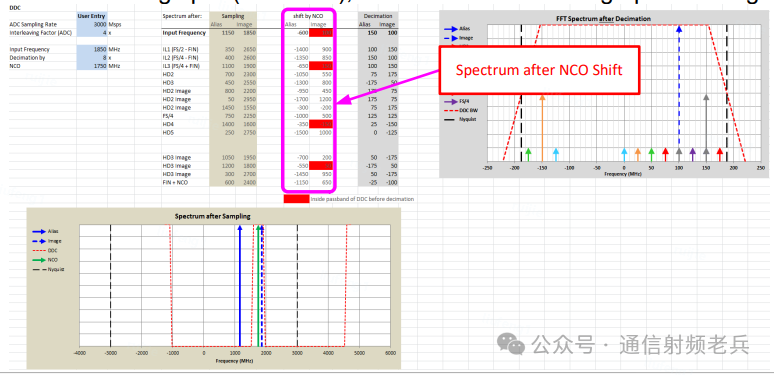
第三步:复数抽取
这一步中,所有落在输出奈奎斯特区边界(±f_out/2)之外的频率,都会通过“频谱旋转”的方式折叠到输出频谱内。这个概念较难理解,举例说明:一个频率略低于 -f_out/2 的信号,会先被衰减,然后从 +f_out/2 开始“旋转”进入输出频谱。
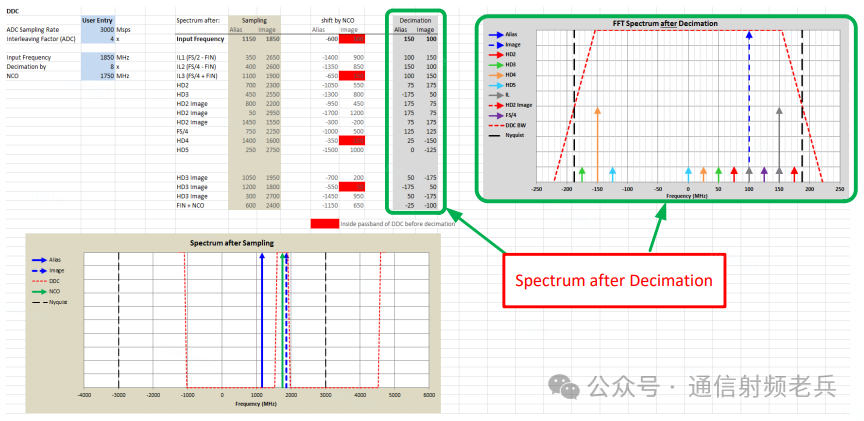
在本例中,输出奈奎斯特区边界为±375MHz。例如,-385MHz的信号,仅比负边界低10MHz,经过抽取后会出现在+365MHz的位置(即距离正边界10MHz处)。
经过NCO移频后,信号的混叠频率是-600MHz,经过抽取旋转后会出现在+150MHz。而其镜像频率移频后是+100MHz,由于已在滤波器通带内,因此不会被旋转。
现在,我们已经计算出了信号和主要杂散经过复数抽取后的最终位置。回头对比FFT测量图,可以看到输入信号明显位于100MHz处,与计算结果完全一致。
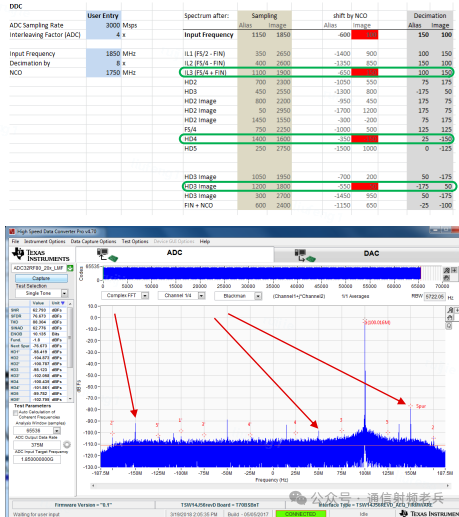
图中还能看到150、50、15、-50、-150MHz的杂散。计算器成功算出了150、50、-150MHz这三个杂散的位置,但15MHz和-50MHz的杂散未被算出。这表明后两者并非源自ADC的2到5次谐波或交织杂散。需要注意的是,我们计算正确的三个杂散,在表格中均被标红,说明它们确实通过了抽取滤波器的通带。
工具下载:
TI频率规划与滤波器计算表格可在官方页面下载。