动态规划精解：LeetCode 516.最长回文子序列问题

理解并高效解决“最长回文子序列”问题，是提升算法与数据结构能力的重要一环。与要求字符连续的回文子串不同，回文子序列允许字符不连续，这为问题增加了一定的复杂度。本文将详细解析如何运用动态规划（DP）思想来解决这个问题。

核心解题思路：动态规划五部曲

动态规划是解决此类最值问题的经典方法，遵循清晰的五步策略可以有效地将思路转化为代码。

1. 确定DP数组含义

首先定义二维DP数组 dp[i][j]，它表示字符串 s 在闭区间 [i, j] 范围内，最长回文子序列的长度。

2. 推导状态转移方程

整个算法的关键在于根据字符 s[i] 与 s[j] 是否相等，进行不同的状态转移。

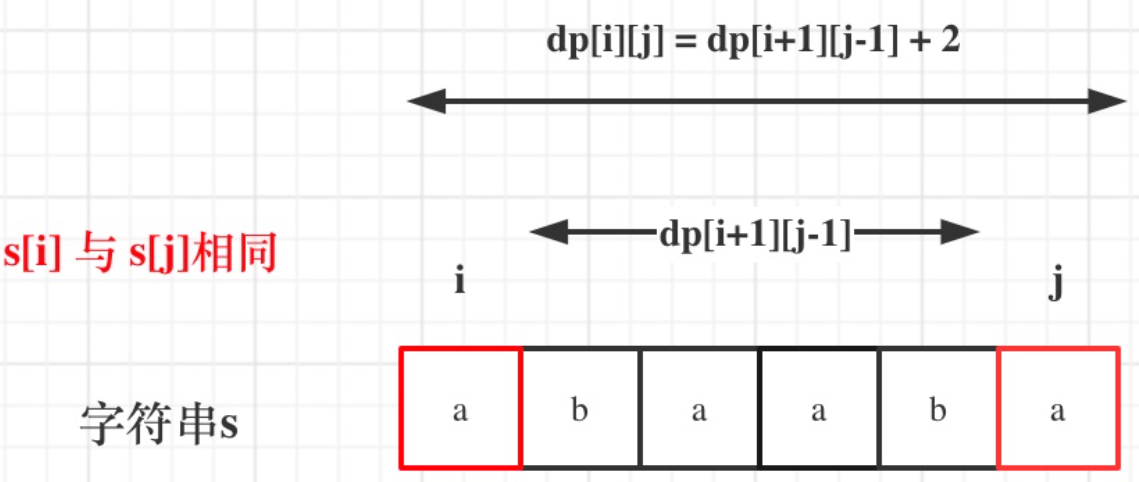
• 情况一：s[i] == s[j]
  当首尾字符相同时，它们必然包含在 [i, j] 区间的最长回文子序列中。因此，区间 [i, j] 的最长长度等于内部区间 [i+1, j-1] 的最长长度加上首尾这两个字符。

  dp[i][j] = dp[i + 1][j - 1] + 2

  

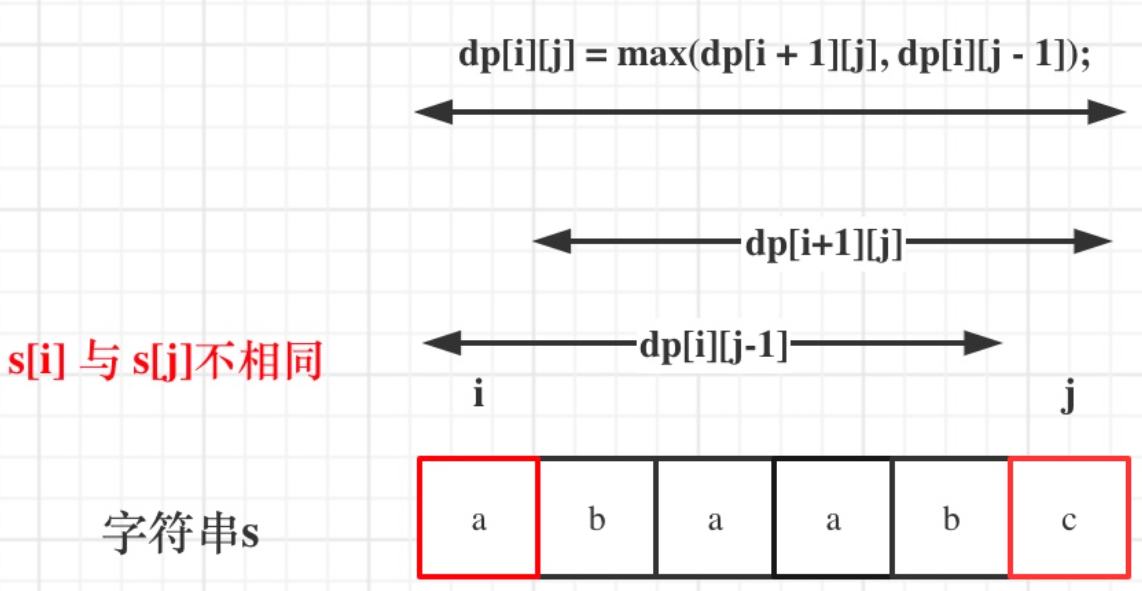
• 情况二：s[i] != s[j]
  当首尾字符不同时，它们不可能同时作为回文子序列的首尾。此时，我们需要考虑分别加入 s[i] 或 s[j] 后，哪个能形成更长的回文子序列。即取两种可能中的最大值。

  dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])

  

将上述逻辑整合，核心递推代码如下：

if (s[i] == s[j]) {
    dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
}

3. 初始化DP数组

递推公式决定了我们需要对基础情况进行初始化：

• 当 i == j 时，即区间内只有一个字符，其本身就是一个长度为1的回文序列。因此 dp[i][i] = 1。
• 对于其他情况（i > j 无意义，i < j 但字符不等的情况），可以将 dp[i][j] 初始化为0，以确保后续取最大值操作不会受到初始值干扰。

4. 确定遍历顺序

观察状态转移方程，dp[i][j] 依赖于其 左下方 (dp[i+1][j-1])、正下方 (dp[i+1][j]) 和 正左方 (dp[i][j-1]) 的值。

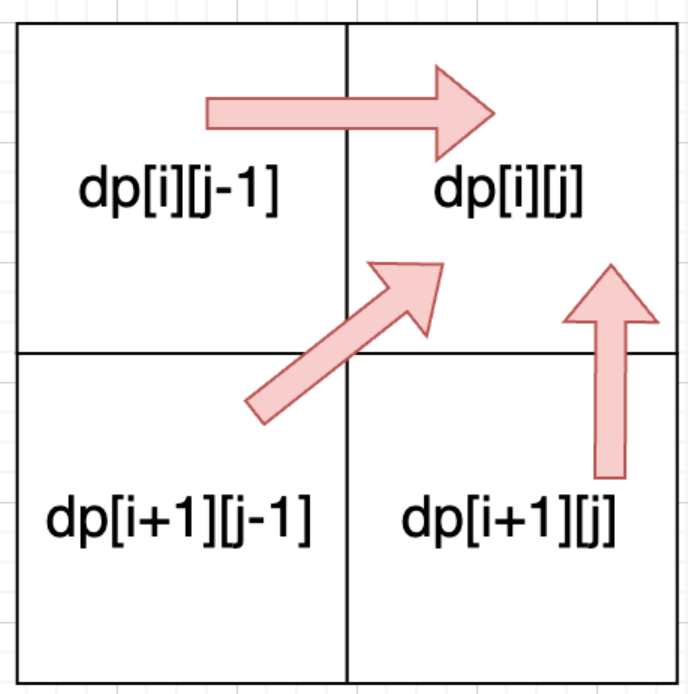
因此，为了保证在计算 dp[i][j] 时其所依赖的状态已被计算，我们必须采用特定的遍历顺序：从下到上（i 递减），从左到右（j 递增）。

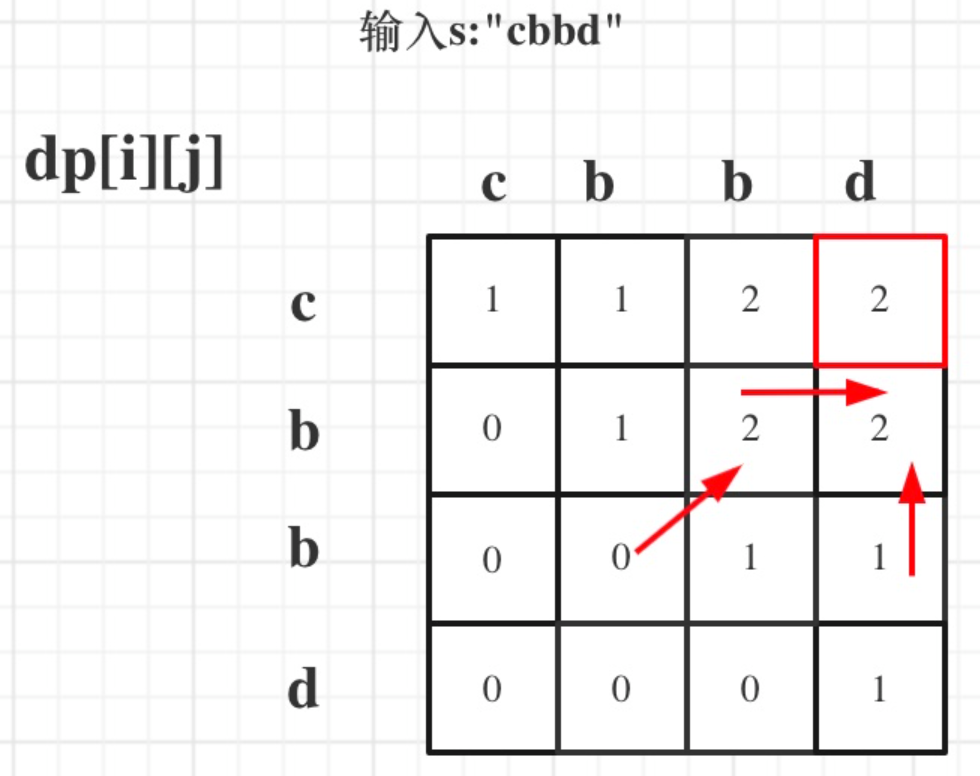
5. 举例推导与验证

以输入 s = "cbbd" 为例，我们可以手动填充DP表来验证算法逻辑。最终 dp[0][3] 的值2即为最长回文子序列（“bb”）的长度。

完整代码实现 (Java)

以下是基于以上动态规划思路的完整Java实现：

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        // dp[i][j] 表示 s[i..j] 的最长回文子序列长度
        int[][] dp = new int[len][len];

        // 遍历顺序：从下到上，从左到右
        for (int i = len - 1; i >= 0; i--) {
            // 初始化单个字符的情况
            dp[i][i] = 1;
            // j 从 i+1 开始，因为 j=i 的情况已初始化
            for (int j = i + 1; j < len; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        // 返回整个字符串 s[0..len-1] 的结果
        return dp[0][len - 1];
    }
}

总结

通过清晰的五步分析，我们将一个看似复杂的字符串问题，系统地拆解为可编程的动态规划状态转移过程。掌握这种分析方法，对于解决LeetCode上的其他区间DP问题（如“最长回文子串”、“扰乱字符串”等）具有重要的借鉴意义。理解并熟练运用Java等语言实现此类算法，是程序员构建扎实基本功的关键。