LeetCode 1514题解：概率最大路径的SPFA算法堆优化实现

本文详细解析 LeetCode 第 1514 题“概率最大的路径”。题目要求在一个加权无向图中，给定每条边的成功概率，找出从起点到终点成功概率最大的路径，并返回该概率值。

问题描述

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图。图的边由列表 edges 描述，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，该边遍历成功的概率为 succProb[i]。

指定起点 start 和终点 end，请找出从起点到终点成功概率最大的路径，并返回其成功概率。如果不存在路径，则返回 0。答案误差不超过 1e-5 即视为正确。

示例 1:

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2，另一条为 0.5 * 0.5 = 0.25

示例 2:

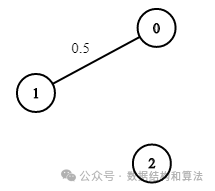
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和节点 2 之间不存在路径

约束条件:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• 每两个节点之间最多有一条边

解题思路

本题核心是计算从起点到终点路径概率的最大值，其中路径概率为各边概率的乘积。这可以视为一个单源最短路径问题的变体，只不过将“距离求和求最小值”变为“概率相乘求最大值”。

我们可以借鉴最短路径算法的思想。由于概率值在[0,1]之间，相乘会导致路径值非递增，因此不能直接使用基于贪心、要求边权非负的迪杰斯特拉算法。一种高效的解决方案是使用 SPFA 算法的堆优化版本。

算法步骤:

1. 建图：使用邻接表存储图结构，每个节点记录其相邻节点及连接边的概率。
2. 初始化：使用一个最大堆（优先队列），根据当前到达节点的概率值排序。将起点(start, 概率1)加入堆中。
3. 搜索：循环从堆中弹出当前概率最大的节点(v, prob)。
   • 若v是终点，则直接返回prob，因为堆保证了这是当前能找到的最大概率。
   • 否则，遍历v的所有邻接节点next_v及边概率next_p。计算从当前路径到达next_v的概率newProb = prob * next_p。
   • 如果newProb大于next_v节点当前已知的概率（可通过一个dist数组维护，初始为0），则更新dist[next_v]，并将(next_v, newProb)加入堆中，等待后续扩展。
4. 终止：若堆为空仍未到达终点，说明终点不可达，返回0。

此方法通过堆不断扩展当前最优路径，并结合概率dist数组的更新来剪枝，避免重复无效计算，效率较高。

代码实现

Java 版本

class Pair implements Comparable<Pair> {
    int v = 0;
    double p = 0;
    public Pair(int v, double p) {
        this.v = v;
        this.p = p;
    }
    @Override
    public int compareTo(Pair pair) {
        // 构造大顶堆，概率大的优先
        return Double.compare(pair.p, this.p);
    }
}

public double maxProbability(int n, int[][] edges, double[] succProb, int start_node, int end_node) {
    // 构建邻接表
    List<Pair>[] g = new List[n];
    for (int i = 0; i < n; i++)
        g[i] = new ArrayList<>();
    for (int i = 0; i < edges.length; i++) {
        int u = edges[i][0];
        int v = edges[i][1];
        double p = succProb[i];
        g[u].add(new Pair(v, p));
        g[v].add(new Pair(u, p));
    }

    double[] dist = new double[n]; // 记录到达每个节点的最大概率
    dist[start_node] = 1.0;
    PriorityQueue<Pair> pq = new PriorityQueue<>();
    pq.offer(new Pair(start_node, 1.0));

    while (!pq.isEmpty()) {
        Pair cur = pq.poll();
        int v = cur.v;
        double prob = cur.p;
        // 如果弹出的不是当前最优概率，则跳过（lazy deletion）
        if (prob < dist[v]) {
            continue;
        }
        if (v == end_node) {
            return prob;
        }
        for (Pair neighbor : g[v]) {
            double newProb = prob * neighbor.p;
            if (newProb > dist[neighbor.v]) {
                dist[neighbor.v] = newProb;
                pq.offer(new Pair(neighbor.v, newProb));
            }
        }
    }
    return 0.0;
}

C++ 版本

#include <vector>
#include <queue>
using namespace std;

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start_node, int end_node) {
        // 构建邻接表， pair<邻居节点, 边概率>
        vector<vector<pair<int, double>>> graph(n);
        for (int i = 0; i < edges.size(); ++i) {
            int u = edges[i][0];
            int v = edges[i][1];
            double p = succProb[i];
            graph[u].emplace_back(v, p);
            graph[v].emplace_back(u, p);
        }

        vector<double> dist(n, 0.0); // 到达各点的最大概率
        dist[start_node] = 1.0;
        // 大顶堆，pair<概率, 节点>
        priority_queue<pair<double, int>> pq;
        pq.emplace(1.0, start_node);

        while (!pq.empty()) {
            auto [curProb, curNode] = pq.top();
            pq.pop();

            // Lazy deletion: 如果堆中存储的不是当前最优值，跳过
            if (curProb < dist[curNode]) {
                continue;
            }
            if (curNode == end_node) {
                return curProb;
            }

            for (auto& [nextNode, edgeProb] : graph[curNode]) {
                double newProb = curProb * edgeProb;
                if (newProb > dist[nextNode]) {
                    dist[nextNode] = newProb;
                    pq.emplace(newProb, nextNode);
                }
            }
        }
        return 0.0;
    }
};

总结

本题的关键在于将“最大成功概率”问题转化为图论中的单源最长路径问题，并利用SPFA算法的思想进行堆优化求解。代码实现中需要注意使用double类型存储概率，并通过dist数组和“惰性删除”技巧来保证算法的正确性与效率。理解这种基于优先队列（堆）的图搜索算法对于解决类似的加权图路径问题非常有帮助。