[面试题] 三个数的最大乘积：Java实现两种解法解析与面试思考

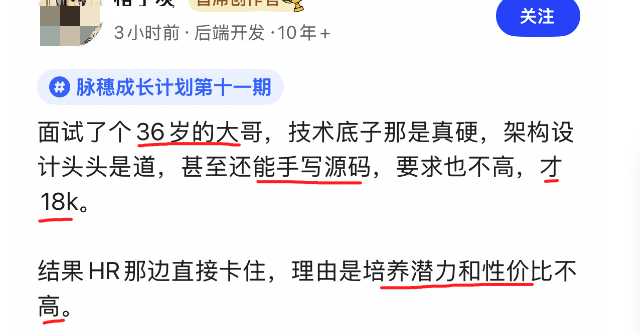
近期一个关于招聘的案例引发了讨论：一家公司面试了一位36岁的工程师，对方技术扎实、精通架构，期望薪资仅为18k，最终却被HR以“培养潜力”和“性价比”为由拒绝。网友们对此看法不一，有人认为存在年龄偏见，也有人觉得是HR与技术评估脱节。

从项目管理的实际经验来看，资深工程师的价值往往体现在代码质量、问题解决效率和高交付能力上。当然，企业招聘有其综合考量，但对于需要独立担当和快速产出的核心岗位，经验与技术深度带来的稳定产出，其价值不容忽视。

回归技术层面，扎实的算法能力是工程师基础素养的体现。下面我们通过一道经典的面试题来探讨一个既需要直觉又需要注意细节的算法问题。

面试题：三个数的最大乘积

给定一个长度大于等于3的整型数组 nums，数组中可能包含正数、负数或零。需要从中选择三个不同下标的数字，计算并返回它们乘积的最大值。

此题的关键在于处理负数：两个负数相乘会得到正数，这常常是解题时容易忽略的突破口。

最直接的思路可能是：“先对数组排序，然后取最大的三个数相乘不就行了？”
假设排序后数组为：[a₁ ≤ a₂ ≤ … ≤ aₙ₋₂ ≤ aₙ₋₁ ≤ aₙ]
一个显而易见的候选答案是：aₙ * aₙ₋₁ * aₙ₋₂（即三个最大的数）。

然而，考虑负数的情况：如果最小的两个数是负数且绝对值很大，例如数组：[-100, -90, 5, 6, 7]

• 三个最大数的乘积：5 * 6 * 7 = 210
• 两个最小负数与最大数的乘积：(-100) * (-90) * 7 = 63000
  显然，后者的结果更大。

因此，我们只需要比较以下两种组合即可：

1. 最大的三个数之积：max1 * max2 * max3
2. 最小的两个数与最大的一个数之积：min1 * min2 * max1
   最终答案就是这两者中的较大值。

解法一：基于排序

思路清晰简单，适合快速实现和理解：

1. 将数组升序排序。
2. 分别计算上述两种情况的乘积。
3. 返回两者中的最大值。

以下是Java实现代码：

import java.util.Arrays;

public class MaxProductOfThree {
    // 排序解法
    public static int maximumProductBySort(int[] nums) {
        // 防御性检查，题目通常保证长度>=3
        if (nums == null || nums.length < 3) {
            throw new IllegalArgumentException("数组长度必须 >= 3");
        }
        Arrays.sort(nums); // 升序排序
        int n = nums.length;
        // 情况一：三个最大数的乘积
        long p1 = 1L * nums[n - 1] * nums[n - 2] * nums[n - 3];
        // 情况二：两个最小数（可能为负）与最大数的乘积
        long p2 = 1L * nums[0] * nums[1] * nums[n - 1];
        // 使用 long 类型计算防止中间结果溢出，最终返回 int
        return (int) Math.max(p1, p2);
    }
}

解法二：线性扫描（O(n)）

如果面试官要求不排序，以 O(n) 时间复杂度解决，则需要进阶解法。事实上，我们只关心五个数：最大的三个数（max1, max2, max3）和最小的两个数（min1, min2）。可以通过一次遍历数组来维护这五个值。

public class MaxProductOfThree {
    // O(n) 单次扫描解法
    public static int maximumProduct(int[] nums) {
        if (nums == null || nums.length < 3) {
            throw new IllegalArgumentException("数组长度必须 >= 3");
        }
        // 初始化
        int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE;
        int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;

        for (int x : nums) {
            // 更新最大的三个数
            if (x >= max1) {
                max3 = max2;
                max2 = max1;
                max1 = x;
            } else if (x >= max2) {
                max3 = max2;
                max2 = x;
            } else if (x >= max3) {
                max3 = x;
            }
            // 更新最小的两个数
            if (x <= min1) {
                min2 = min1;
                min1 = x;
            } else if (x <= min2) {
                min2 = x;
            }
        }
        long p1 = 1L * max1 * max2 * max3;
        long p2 = 1L * min1 * min2 * max1;
        return (int) Math.max(p1, p2);
    }

    // 测试用例
    public static void main(String[] args) {
        int[] nums1 = {-10, -10, 1, 2, 3};
        System.out.println(maximumProduct(nums1)); // 预期输出 300
        int[] nums2 = {1, 2, 3, 4};
        System.out.println(maximumProduct(nums2)); // 预期输出 24
    }
}

总结

这道题的核心结论是：最大乘积只可能来源于「最大的三个数」或「最小的两个数乘以最大的数」这两种组合之一。 掌握这一结论后，无论是写出简洁的排序解法，还是在线性扫描解法中熟练维护最大值和最小值，都能在面试中从容应对。技术能力的深度，往往就体现在对这些基础问题透彻的理解和稳健的实现上。