LeetCode矩阵算法精讲：从旋转图像到岛屿数量，掌握二维数组核心技巧

在算法学习与面试准备中，二维数组（矩阵）相关的问题因其直观性和复杂性，是检验编程与思维能力的绝佳试金石。本文系统梳理了LeetCode及剑指Offer中一系列经典的矩阵问题，从基础的矩阵操作（旋转、置零），到基于深度优先搜索（DFS）、广度优先搜索（BFS）的路径与连通域问题，逐一剖析解题思路与高效实现。掌握这些问题的解法，能帮助你深入理解Python在处理复杂数据结构时的灵活性与强大威力，是攻克技术面试、提升算法功底的必经之路。

一、经典矩阵操作问题

1. 旋转图像 (Rotate Image)

问题：给定一个 n × n 的二维矩阵，代表一个图像。请你将图像顺时针旋转90度。必须原地修改输入矩阵。

解题思路：
可以通过两次翻转实现顺时针90度旋转：

1. 水平翻转：将矩阵上下对调。
2. 主对角线翻转：将矩阵沿左上-右下对角线对称交换。

代码实现 (C++)：

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 1. 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - 1 - i][j]);
            }
        }
        // 2. 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

复杂度分析：

• 时间复杂度：O(n²)，需要遍历矩阵中的每个元素。
• 空间复杂度：O(1)，只使用了常数级的额外空间。

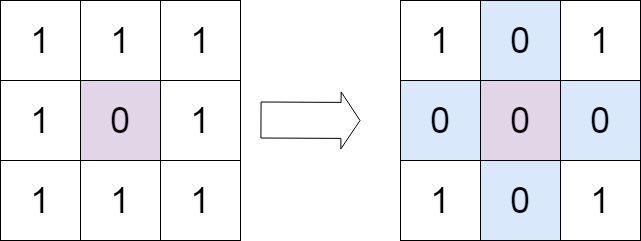
2. 矩阵置零 (Set Matrix Zeroes)

问题：给定一个 m x n 的矩阵，如果一个元素为 0，则将其所在行和列的所有元素都设为 0。要求使用原地算法。

进阶要求：使用常量空间复杂度。

解题思路（常量空间）：
核心思想是利用矩阵的第一行和第一列来记录该行/列是否需要置零。为了不破坏第一行和第一列的标记信息，需要额外的变量来单独处理第一行和第一列的情况。

1. 使用两个布尔变量记录第一行和第一列本身是否包含0。
2. 遍历矩阵（从第二行第二列开始），如果发现matrix[i][j] == 0，则将matrix[i][0]和matrix[0][j]标记为0。
3. 再次遍历矩阵，根据第一行和第一列的标记信息，将对应元素置零。
4. 最后，根据第一步的布尔变量，处理第一行和第一列。

代码实现 (Python)：

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        m, n = len(matrix), len(matrix[0])
        first_row_has_zero = any(matrix[0][j] == 0 for j in range(n))
        first_col_has_zero = any(matrix[i][0] == 0 for i in range(m))

        # 使用第一行和第一列作为标记
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0
                    matrix[0][j] = 0

        # 根据标记置零
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0

        # 处理第一行和第一列
        if first_row_has_zero:
            for j in range(n):
                matrix[0][j] = 0
        if first_col_has_zero:
            for i in range(m):
                matrix[i][0] = 0

复杂度分析：

• 时间复杂度：O(m × n)
• 空间复杂度：O(1)

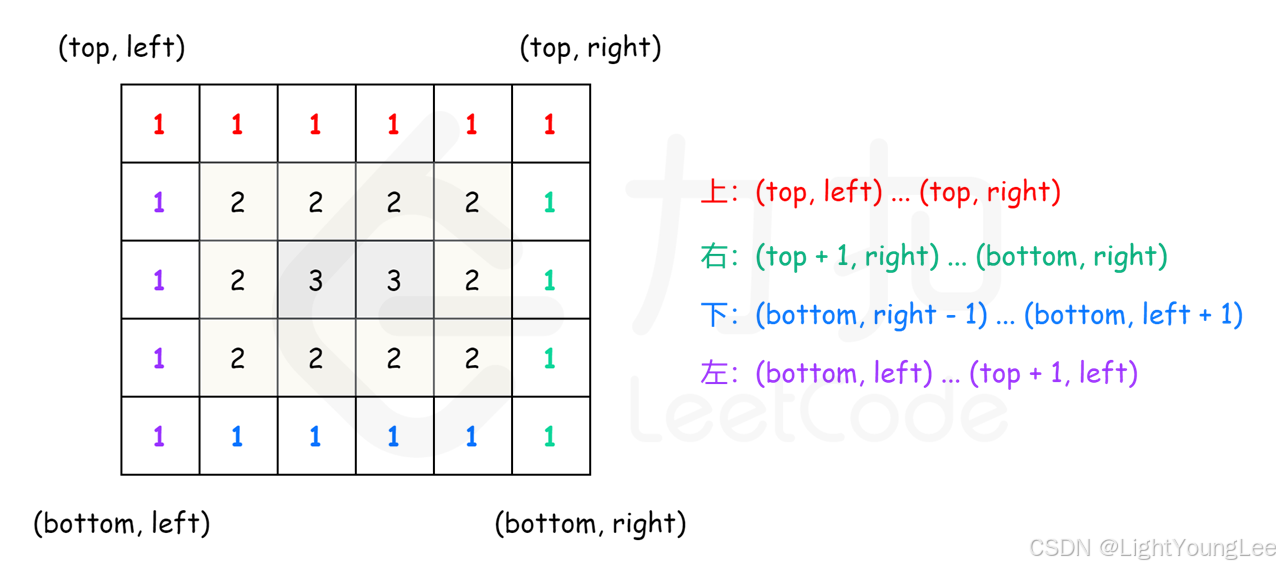
3. 螺旋矩阵 (Spiral Matrix)

问题：给定一个 m x n 矩阵，按螺旋顺序返回矩阵中的所有元素。

解题思路：
模拟螺旋遍历的过程。可以想象矩阵是由一层层“圈”组成的。我们定义四个边界：top, bottom, left, right。

1. 从左到右遍历上边界 (top行)，遍历完top++。
2. 从上到下遍历右边界 (right列)，遍历完right--。
3. 如果此时top <= bottom，从右到左遍历下边界 (bottom行)，遍历完bottom--。
4. 如果此时left <= right，从下到上遍历左边界 (left列)，遍历完left++。
   重复以上步骤，直到边界交错。

代码实现 (Python)：

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix:
            return []
        m, n = len(matrix), len(matrix[0])
        top, bottom, left, right = 0, m - 1, 0, n - 1
        res = []
        while top <= bottom and left <= right:
            # 上边界
            for j in range(left, right + 1):
                res.append(matrix[top][j])
            top += 1
            # 右边界
            for i in range(top, bottom + 1):
                res.append(matrix[i][right])
            right -= 1
            # 下边界 (需要判断是否还存在有效行)
            if top <= bottom:
                for j in range(right, left - 1, -1):
                    res.append(matrix[bottom][j])
                bottom -= 1
            # 左边界 (需要判断是否还存在有效列)
            if left <= right:
                for i in range(bottom, top - 1, -1):
                    res.append(matrix[i][left])
                left += 1
        return res

复杂度分析：

• 时间复杂度：O(m × n)
• 空间复杂度：O(1) (不计入结果数组)

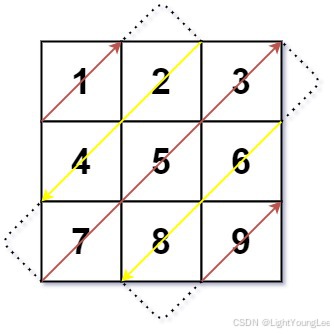
4. 对角线遍历 (Diagonal Traverse)

问题：给定一个 m x n 矩阵，以对角线顺序返回所有元素。方向交替变化。

解题思路：
所有对角线编号 i 的范围是 [0, m+n-2]。根据对角线编号的奇偶性决定遍历方向：

• 奇数对角线：从左上向右下遍历 (row++, col--)。
• 偶数对角线：从右下向左上遍历 (row--, col++)。
  关键是确定每条对角线的起点坐标，并在遍历时注意矩阵边界。

代码实现 (Python)：

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        m, n = len(mat), len(mat[0])
        res = []
        for i in range(m + n - 1):
            if i % 2 == 0:  # 偶数对角线，从下往上
                x = i if i < m else m - 1
                y = i - x
                while x >= 0 and y < n:
                    res.append(mat[x][y])
                    x -= 1
                    y += 1
            else:  # 奇数对角线，从上往下
                y = i if i < n else n - 1
                x = i - y
                while x < m and y >= 0:
                    res.append(mat[x][y])
                    x += 1
                    y -= 1
        return res

复杂度分析：

• 时间复杂度：O(m × n)
• 空间复杂度：O(1) (不计入结果数组)

二、深度/广度优先搜索应用

1. 单词搜索 (Word Search)

问题：给定一个字符矩阵和一个单词，判断单词是否存在于网格中。单词必须由相邻单元格（水平或垂直）的字母按顺序构成，同一个单元格内的字母不允许重复使用。

解题思路：
典型的回溯法（DFS） 应用。对于矩阵中的每个起点，尝试进行深度优先搜索。

1. 定义递归函数dfs(i, j, k)，表示从(i, j)出发，能否匹配单词的第k个字符。
2. 终止条件：k == len(word)，说明全部匹配成功，返回True。
3. 边界/条件判断：位置越界、字符不匹配、或该位置已访问过，则返回False。
4. 标记当前位置为已访问。
5. 向四个方向（上、下、左、右）进行递归搜索。
6. 回溯：取消当前位置的访问标记（因为其他路径可能用到）。
7. 遍历所有起点，任何一个起点能成功则返回True。

代码实现 (Python)：

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        m, n = len(board), len(board[0])
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        visited = [[False] * n for _ in range(m)]

        def dfs(i, j, k):
            # 终止条件：完全匹配
            if k == len(word):
                return True
            # 边界或条件判断
            if not (0 <= i < m and 0 <= j < n) or visited[i][j] or board[i][j] != word[k]:
                return False

            # 标记并搜索
            visited[i][j] = True
            for di, dj in directions:
                if dfs(i + di, j + dj, k + 1):
                    return True
            # 回溯
            visited[i][j] = False
            return False

        # 尝试每个起点
        for i in range(m):
            for j in range(n):
                if dfs(i, j, 0):
                    return True
        return False

复杂度分析：

• 时间复杂度：最坏情况 O(m × n × 3^L)，其中 L 为单词长度。每个起点开始搜索，每一步有3个方向（除去来路）。
• 空间复杂度：O(m × n) (用于访问标记) + O(L) (递归栈深度)。

2. 岛屿数量 (Number of Islands)

问题：给定一个由 '1'（陆地）和 '0'（水）组成的二维网格，计算岛屿的数量。岛屿由水平或垂直方向上相邻的陆地连接形成，假设网格四边都被水包围。

解题思路：
深度优先搜索（DFS） 或广度优先搜索（BFS） 的经典“连通分量”问题。遍历网格，当遇到一个 '1'（陆地）时：

1. 岛屿计数加一。
2. 以该陆地为起点，进行DFS或BFS，将所有与之相连的陆地标记为已访问（例如，将 '1' 改为 '0'），从而避免重复计数。
3. 继续遍历网格，寻找下一个未被访问的陆地。

代码实现 (DFS, Python)：

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        if not grid:
            return 0
        m, n = len(grid), len(grid[0])

        def dfs(i, j):
            # 将当前陆地淹没（标记为已访问）
            grid[i][j] = '0'
            # 遍历四个方向
            for di, dj in [(0,1), (0,-1), (1,0), (-1,0)]:
                ni, nj = i + di, j + dj
                if 0 <= ni < m and 0 <= nj < n and grid[ni][nj] == '1':
                    dfs(ni, nj)

        count = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == '1':
                    count += 1
                    dfs(i, j)
        return count

复杂度分析：

• 时间复杂度：O(m × n)，每个单元格最多被访问一次。
• 空间复杂度：O(min(m, n))，最坏情况下递归栈的深度。对于BFS，队列的空间复杂度也为 O(min(m, n))。

3. 岛屿的最大面积 (Max Area of Island)

问题：在给定的二进制矩阵中，找到最大岛屿的面积（即相连的 1 的数量）。

解题思路：
与“岛屿数量”问题类似，但在DFS/BFS过程中，需要计算并返回当前岛屿的面积，并在主函数中维护一个最大值。

代码实现 (DFS, Python)：

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])

        def dfs(i, j):
            if not (0 <= i < m and 0 <= j < n) or grid[i][j] == 0:
                return 0
            grid[i][j] = 0  # 淹没陆地
            area = 1
            for di, dj in [(0,1), (0,-1), (1,0), (-1,0)]:
                area += dfs(i + di, j + dj)
            return area

        max_area = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    max_area = max(max_area, dfs(i, j))
        return max_area

复杂度分析：与“岛屿数量”相同。

4. 矩阵中的最长递增路径 (Longest Increasing Path in a Matrix)

问题：给定一个整数矩阵，找出其最长递增路径的长度。对于每个单元格，可以向上下左右四个方向移动，但不能沿对角线移动或移出边界。

解题思路：
记忆化深度优先搜索（DFS + Memoization）。这是此类“矩阵中寻找最长路径”问题的典型解法。

1. 定义dfs(i, j)函数，返回从(i, j)出发的最长递增路径长度。
2. 如果(i, j)的结果已经计算过（存储在记忆化数组memo中），则直接返回。
3. 否则，初始化长度为1（路径至少包含自身）。向四个方向探索，如果邻居的值严格大于当前值，则递归计算从邻居出发的长度，并更新当前最大长度：1 + dfs(ni, nj)。
4. 将结果存入memo[i][j]并返回。
5. 遍历所有单元格作为起点，取最大值。

代码实现 (Python)：

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        if not matrix:
            return 0
        m, n = len(matrix), len(matrix[0])
        memo = [[0] * n for _ in range(m)]  # 记忆化数组
        directions = [(0,1), (0,-1), (1,0), (-1,0)]

        def dfs(i, j):
            if memo[i][j] != 0:
                return memo[i][j]
            max_len = 1
            for di, dj in directions:
                ni, nj = i + di, j + dj
                if 0 <= ni < m and 0 <= nj < n and matrix[ni][nj] > matrix[i][j]:
                    max_len = max(max_len, 1 + dfs(ni, nj))
            memo[i][j] = max_len
            return max_len

        longest = 0
        for i in range(m):
            for j in range(n):
                longest = max(longest, dfs(i, j))
        return longest

复杂度分析：

• 时间复杂度：O(m × n)。每个单元格的计算结果被缓存，最多计算一次。
• 空间复杂度：O(m × n)，用于存储memo数组和递归栈深度。

5. 迷宫中的最近出口 (Nearest Exit from Entrance in Maze)

问题：给定一个表示迷宫的矩阵，包含空单元格（.）和墙（+）。你站在入口entrance。每一步可以向上下左右移动一格，不能穿墙或出界。目标是找到最近的出口。出口定义为位于迷宫边界的空单元格，入口不算出口。

解题思路：
典型的广度优先搜索（BFS） 求最短路径问题。BFS天然保证了第一次到达出口时，路径长度是最短的。

1. 将入口坐标和初始步数0加入队列，并将入口标记为已访问（可改为墙+）。
2. 当队列不为空时，弹出队首元素(x, y, steps)。
3. 遍历其四个邻居，如果邻居是有效空单元格（.），则判断其是否在边界且不是入口。如果是，则返回steps + 1。
4. 如果不是出口，则将其标记为已访问并加入队列，步数为steps + 1。
5. 如果BFS结束仍未找到出口，返回-1。

代码实现 (Python)：

from collections import deque
class Solution:
    def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:
        m, n = len(maze), len(maze[0])
        directions = [(0,1), (0,-1), (1,0), (-1,0)]
        queue = deque()
        ex, ey = entrance
        maze[ex][ey] = '+'  # 标记入口为已访问
        queue.append((ex, ey, 0))

        while queue:
            x, y, steps = queue.popleft()
            # 遍历四个方向
            for dx, dy in directions:
                nx, ny = x + dx, y + dy
                # 检查邻居是否有效且为空
                if 0 <= nx < m and 0 <= ny < n and maze[nx][ny] == '.':
                    # 检查是否为出口 (在边界上)
                    if nx == 0 or nx == m-1 or ny == 0 or ny == n-1:
                        return steps + 1
                    # 不是出口，标记并加入队列
                    maze[nx][ny] = '+'
                    queue.append((nx, ny, steps + 1))
        return -1

复杂度分析：

• 时间复杂度：O(m × n)，每个单元格最多入队一次。
• 空间复杂度：O(min(m, n))，BFS队列在最坏情况下的空间开销。

6. 二进制矩阵中的最短路径 (Shortest Path in Binary Matrix)

问题：给定一个 n x n 的二进制矩阵，返回从左上角(0, 0)到右下角(n-1, n-1)的最短畅通路径的长度。路径需满足：所有单元格值为0，且相邻单元格是8方向连通的（共享边或角）。如果不存在这样的路径，返回 -1。

解题思路：
同样是BFS求最短路径，但移动方向从4个变为8个。注意起点或终点如果是1，则直接返回-1。

代码实现 (Python)：

from collections import deque
class Solution:
    def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
        n = len(grid)
        if grid[0][0] == 1 or grid[n-1][n-1] == 1:
            return -1
        # 8个方向
        directions = [(-1,-1), (-1,0), (-1,1), (0,-1), (0,1), (1,-1), (1,0), (1,1)]
        queue = deque()
        queue.append((0, 0, 1))  # (x, y, path_length)
        grid[0][0] = 1  # 标记为已访问

        while queue:
            x, y, length = queue.popleft()
            if x == n-1 and y == n-1:
                return length
            for dx, dy in directions:
                nx, ny = x + dx, y + dy
                if 0 <= nx < n and 0 <= ny < n and grid[nx][ny] == 0:
                    grid[nx][ny] = 1  # 标记为已访问
                    queue.append((nx, ny, length + 1))
        return -1

复杂度分析：

• 时间复杂度：O(n²)。
• 空间复杂度：O(n²)，最坏情况下队列可能存储大部分节点。

三、进阶与综合应用

1. 搜索二维矩阵 II (Search a 2D Matrix II) / 剑指 Offer 04. 二维数组中的查找

问题：在一个 m x n 的矩阵中，每一行从左到右递增，每一列从上到下递增。请完成一个高效函数，判断数组中是否含有目标整数。

解题思路：
利用矩阵的排序特性，从矩阵的右上角（或左下角）开始搜索。

• 从右上角(0, n-1)开始：
  • 如果target < matrix[row][col]，说明目标值不可能在当前列（该列以下都更大），col--。
  • 如果target > matrix[row][col]，说明目标值不可能在当前行（该行以左都更小），row++。
  • 如果相等，返回True。
• 直到行或列索引越界。

代码实现 (Python)：

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix:
            return False
        m, n = len(matrix), len(matrix[0])
        row, col = 0, n - 1  # 从右上角开始
        while row < m and col >= 0:
            if matrix[row][col] == target:
                return True
            elif matrix[row][col] < target:
                row += 1  # 目标值更大，下移一行
            else:
                col -= 1  # 目标值更小，左移一列
        return False

复杂度分析：

• 时间复杂度：O(m + n)，每次循环排除一行或一列。
• 空间复杂度：O(1)。

2. 有序矩阵中第 K 小的元素 (Kth Smallest Element in a Sorted Matrix)

问题：给定一个 n x n 矩阵，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。

解题思路：
二分查找法。矩阵的最小值left在左上角matrix[0][0]，最大值right在右下角matrix[n-1][n-1]。

1. 在[left, right]区间内进行二分查找，设mid = (left + right) // 2。
2. 统计矩阵中小于等于mid的元素个数count。可以利用矩阵的性质从左下角开始线性统计：
   • 如果matrix[i][j] <= mid，那么该行j列及其左边的所有元素都<= mid，count += (j+1)，然后i++（向上移动）。
   • 如果matrix[i][j] > mid，则j--（向左移动）。
3. 如果count >= k，说明第k小的元素在左半部分（<= mid），令right = mid。
4. 否则，说明第k小的元素在右半部分，令left = mid + 1。
5. 循环结束时，left即为第k小的元素。

代码实现 (Python)：

class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix)
        left, right = matrix[0][0], matrix[-1][-1]

        def count_less_equal(mid):
            # 从左下角开始统计
            i, j = n - 1, 0
            cnt = 0
            while i >= 0 and j < n:
                if matrix[i][j] <= mid:
                    cnt += (i + 1)  # 这一列从0到i行的元素都<=mid
                    j += 1
                else:
                    i -= 1
            return cnt

        while left < right:
            mid = (left + right) // 2
            if count_less_equal(mid) >= k:
                right = mid
            else:
                left = mid + 1
        return left

复杂度分析：

• 时间复杂度：O(n log(max-min))，其中max和min是矩阵中的最大和最小值。每次统计count需要O(n)。
• 空间复杂度：O(1)。

3. 合并账户 (Accounts Merge)

问题：给定一个账户列表，每个账户的第一个元素是名字，后面是邮箱地址。如果两个账户有共同的邮箱，则它们属于同一个人。需要合并属于同一个人的所有账户，并按照指定格式返回（名字+排序后的邮箱）。

解题思路：
这是一个连通分量问题，可以使用并查集 (Union-Find) 高效解决。

1. 为每个邮箱分配一个唯一索引。
2. 遍历每个账户，将账户内的所有邮箱在并查集中进行合并（连接到第一个邮箱）。
3. 合并完成后，通过并查集的根节点将属于同一人的邮箱归集到一起。
4. 对每个集合的邮箱排序，加上账户名，构成最终结果。

代码实现 (Python)：

from collections import defaultdict
class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    def union(self, x, y):
        rootX, rootY = self.find(x), self.find(y)
        if rootX != rootY:
            self.parent[rootY] = rootX

class Solution:
    def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
        email_to_id = {}
        email_to_name = {}
        id_counter = 0

        # 建立邮箱到ID的映射
        for acc in accounts:
            name = acc[0]
            for email in acc[1:]:
                if email not in email_to_id:
                    email_to_id[email] = id_counter
                    email_to_name[email] = name
                    id_counter += 1

        uf = UnionFind(id_counter)
        # 合并同一账户内的邮箱
        for acc in accounts:
            first_email_id = email_to_id[acc[1]]
            for email in acc[2:]:
                uf.union(first_email_id, email_to_id[email])

        # 根据根ID归集邮箱
        id_to_emails = defaultdict(list)
        for email, eid in email_to_id.items():
            root_id = uf.find(eid)
            id_to_emails[root_id].append(email)

        # 构造结果
        res = []
        for emails in id_to_emails.values():
            name = email_to_name[emails[0]]
            res.append([name] + sorted(emails))
        return res

复杂度分析：

• 时间复杂度：O(N log N) 或 O(N α(N))，其中N为所有邮箱数量，α为阿克曼函数的反函数，近乎常数。主要开销在排序。
• 空间复杂度：O(N)。

4. 课程表 (Course Schedule)

问题：必须选修 numCourses 门课，某些课有先修要求（用 prerequisites 数组表示）。判断是否可能完成所有课程（即判断有向图是否存在环）。

解题思路：
经典的拓扑排序问题，可以转化为判断有向图是否存在环。

• DFS方法：使用状态数组visited（0=未访问，1=访问中，2=已访问）。对每个节点进行DFS，如果在DFS过程中遇到状态为1的节点，说明存在环。
• BFS方法 (Kahn算法)：计算每个节点的入度。将所有入度为0的节点加入队列。依次从队列中取出节点，将其所有邻居的入度减1，若邻居入度变为0则加入队列。如果最终所有节点都被取出，则图无环；否则，存在环。

代码实现 (BFS, Python)：

from collections import deque
class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        # 构建邻接表和入度数组
        graph = [[] for _ in range(numCourses)]
        indegree = [0] * numCourses
        for course, pre in prerequisites:
            graph[pre].append(course)
            indegree[course] += 1

        # BFS拓扑排序
        queue = deque([i for i in range(numCourses) if indegree[i] == 0])
        visited = 0
        while queue:
            node = queue.popleft()
            visited += 1
            for neighbor in graph[node]:
                indegree[neighbor] -= 1
                if indegree[neighbor] == 0:
                    queue.append(neighbor)

        return visited == numCourses

复杂度分析：

• 时间复杂度：O(V + E)，其中V为课程数，E为先修要求数。
• 空间复杂度：O(V + E)，用于存储邻接表和入度数组。

5. 电话号码的字母组合 (Letter Combinations of a Phone Number)

问题：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合（数字到字母的映射如同电话按键）。

解题思路：
典型的回溯法。可以将其视为在树形结构上的深度优先搜索。

1. 建立数字到字母串的映射字典。
2. 定义一个回溯函数backtrack(index, path)，其中index表示当前处理到输入数字的第几位，path是当前已构建的字符串。
3. 终止条件：index == len(digits)，将path加入结果列表。
4. 否则，取出当前数字对应的字母串，遍历每个字母，将其加入path，然后递归调用backtrack(index+1, new_path)，之后进行回溯（path弹出最后一个字母）。

代码实现 (Python)：

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        if not digits:
            return []
        phone_map = {
            '2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
            '6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'
        }
        res = []
        def backtrack(index, path):
            if index == len(digits):
                res.append(''.join(path))
                return
            for letter in phone_map[digits[index]]:
                path.append(letter)
                backtrack(index + 1, path)
                path.pop()  # 回溯
        backtrack(0, [])
        return res

复杂度分析：

• 时间复杂度：O(3^m × 4^n)，其中m是对应3个字母的数字个数，n是对应4个字母的数字个数。
• 空间复杂度：O(m+n)，递归调用栈的深度。

四、其他精选题目

除了上述核心题目，还有一些值得关注的矩阵问题，其解法同样富有启发性：

• 827. 最大人工岛：在0和1组成的网格中，允许将一个0变成1，求操作后可能的最大岛屿面积。解法通常涉及两次DFS：第一次标记并计算每个岛屿的面积；第二次遍历每个0，计算将其变为1后能连接周围不同岛屿的总面积。

• 302. 包含黑像素的最小矩形：给定一个只包含一个黑色区域的二进制图像，以及一个黑像素的坐标，要求用低于 O(mn) 的复杂度找到包含所有黑像素的最小矩形。通常使用二分查找分别确定矩形的上下左右边界。

• 317. 离所有建筑物最近的距离：在网格中标记了建筑物1、空地0和障碍2，找到一块空地，使其到所有建筑物的曼哈顿距离之和最小。可以通过从每个建筑物出发进行BFS，累计所有空地到建筑物的距离和访问次数来解决。

• 1074. 元素和为目标值的子矩阵数量：计算矩阵中和为目标值的子矩阵个数。通常使用前缀和 + 哈希表的技巧，将其优化为 O(m² × n) 或 O(n² × m) 的复杂度。

掌握这些二维数组问题的核心解法，不仅能帮助你在算法面试中游刃有余，更能深刻理解搜索、动态规划、并查集等基础算法思想在具体场景下的灵活应用。持续练习与总结，是提升算法能力的不二法门。