卡尔曼滤波器原理与Python实现：从状态估计到自动驾驶应用

数据有噪声，导致预测不准？掌握卡尔曼滤波器算法，能让你的系统感知与预测更智能。

你是否曾经遇到过这样的场景：无人机在空中晃动，GPS数据跳来跳去；自动驾驶汽车的摄像头、雷达传感器读数相互矛盾；机器人定位时，里程计和激光雷达数据对不上……

这些问题的核心，都是如何从充满噪声和不确定性的数据流中，提取出最接近真实的信号。

今天要深入剖析的卡尔曼滤波器（Kalman Filter），正是解决这类状态估计问题的“数学瑞士军刀”。它能优雅地融合系统模型的预测与传感器的实时测量，在不确定性中给出最优估计。

一、卡尔曼滤波器：核心思想与定义

卡尔曼滤波器是一种递归算法，用于动态估计系统随时间变化的“状态”（如位置、速度等），即使在传感器数据不精确、系统模型不完全准确的情况下。

这里的“状态”可以是你关心的任何随时间变化的物理量：

• 位置（一维坐标、GPS经纬度）
• 速度、加速度
• 方向、角度（姿态）
• 温度、压力等系统参数

其核心思想可以类比为一位经验丰富的航海家：他会根据船只的当前航速和航向（基于模型的预测），结合间歇观测到的灯塔方位（带有误差的测量），在脑海中持续推算出最可能的航线。预测提供了状态的连续性，测量则用于修正累积的偏差，两者反复结合，使得估计路线越来越精准。

二、直观理解：从一维贝叶斯更新开始

卡尔曼滤波器的数学根基是贝叶斯推理。我们先用一个极度简化的一维定位场景来感受它的工作原理。

想象你在一条长走廊里蒙眼行走，只能依靠偶尔触摸墙壁来感知位置。此时你有两个信息来源：

1. 你的步伐（预测）：根据步数和已知步长，你推测自己大概走了10米，但这个推测并不精确（方差较大）。
2. 你的触觉（测量）：你摸到墙上的一个特殊标志，感觉它大约在12米处，但触觉也可能出错（测量也存在误差）。

卡尔曼滤波器会怎么做？它不会武断地取平均值(11米)，而是进行“最优加权平均”：哪个信息来源的不确定性更小（方差小），就在最终估计中赋予它更大的权重。神奇的是，融合后的估计，其确定性（置信度）会比任何一个单独的信息来源都高！

下图直观展示了一维卡尔曼滤波中的贝叶斯更新过程，揭示了先验估计与新观测如何结合，形成更清晰的后验估计。

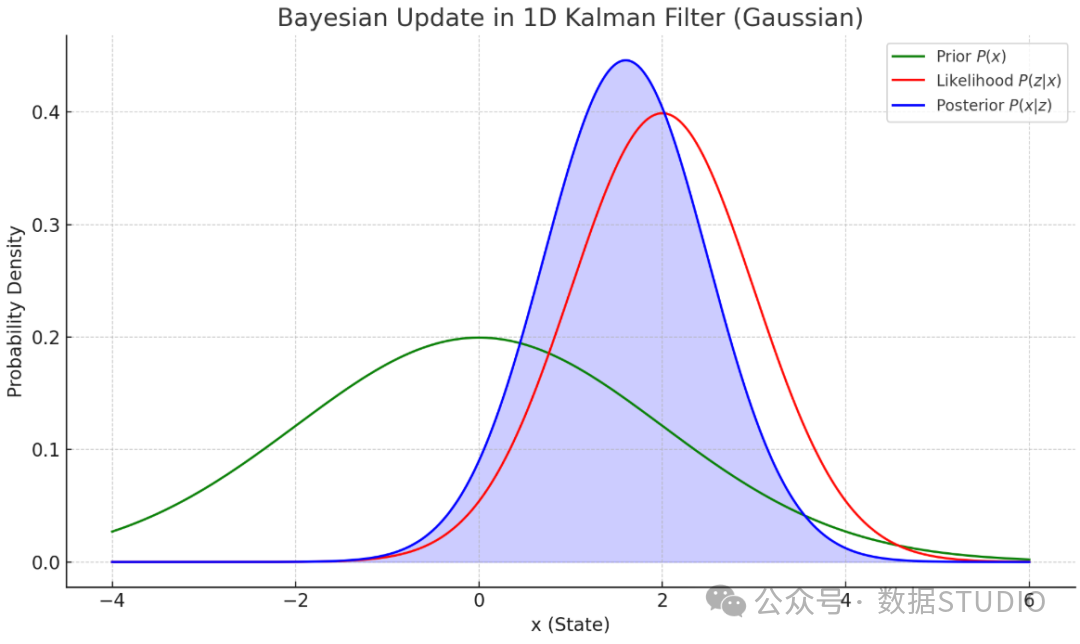
• 先验信念：在纳入新测量值之前对状态的估计，具有均值（如来自预测）和方差（不确定性）。
• 测量似然：表示在真实状态为 x 的情况下观察到测量值 z 的概率分布，通常传感器精度较高，其方差较小。
• 后验估计：结合了先验与测量两种信息来源的新估计。其均值会移动到先验均值与测量值之间的某个位置，而方差显著减小，因为你掌握了更多信息。

不确定性为何会减少？

卡尔曼滤波器最强大的特性之一，就是能通过融合信息来降低总体不确定性。更新后的（后验）方差计算公式为：

$σ_{new}^2 = \frac{1}{ \frac{1}{σ_{prior}^2} + \frac{1}{σ_{meas}^2} }$

其中 $σ_{prior}^2$ 是先验方差，$σ_{meas}^2$ 是测量方差。该公式保证了：

$σ_{new}^2 < min(σ_{prior}^2, σ_{meas}^2)$

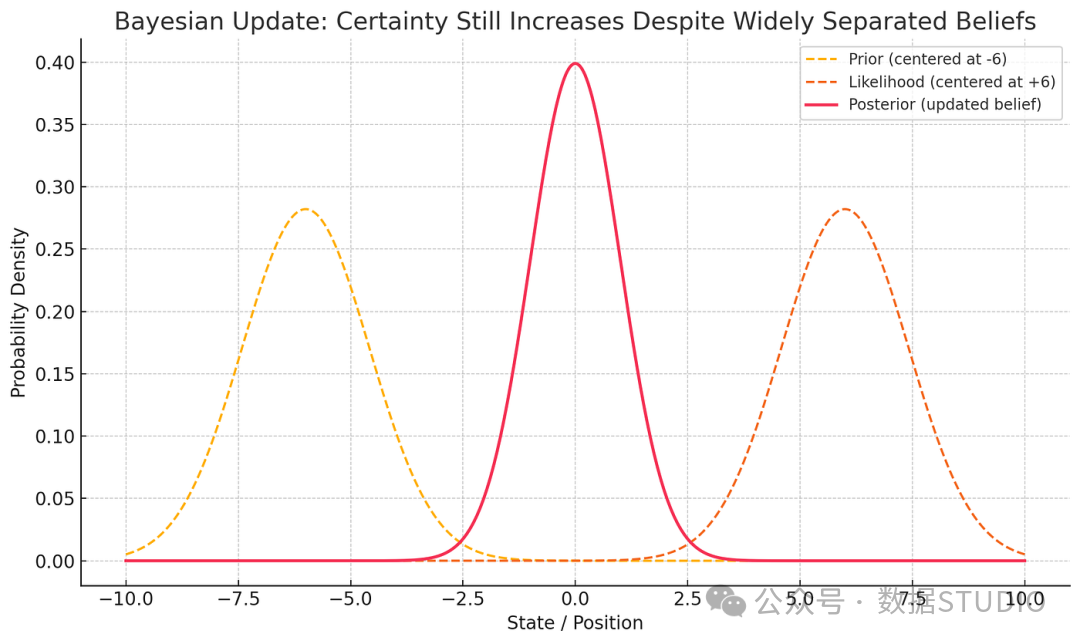
更新后的信念（后验）总是比单独的预测或测量更加确定。即使在先验和测量值相差较远时，它也能产生更可靠的估计。

代码实践：一维卡尔曼滤波模拟

下面的Python代码完美诠释了这个过程。我们从一个不确定性极高的初始位置猜测开始，通过反复执行“预测-更新”循环，你会观察到不确定性（方差）像雪崩般迅速收敛。

# 1D卡尔曼滤波核心函数
# 测量更新：融合先验估计与新的观测值
def update_belief(prior_mean, prior_var, meas_value, meas_var):
    """
    参数:
    prior_mean: 预测的平均值 (μ_prior)
    prior_var:  预测的方差 (σ²_prior)
    meas_value: 测量值 (z)
    meas_var:   测量的方差 (σ²_meas)

    返回:
    [新的平均值, 新的方差]
    """
    # 核心公式：加权平均，权重为方差的倒数（不确定性越小，权重越大）
    combined_mean = (meas_var * prior_mean + prior_var * meas_value) / (prior_var + meas_var)
    # 新方差：融合后信息更多，不确定性必然降低
    combined_var = 1 / (1 / prior_var + 1 / meas_var)
    return [combined_mean, combined_var]

# 预测步骤：根据运动模型预测下一个状态
def predict_state(current_mean, current_var, motion_change, motion_var):
    """
    参数:
    motion_change: 控制输入或预计的移动量 (u)
    motion_var:    运动模型的不确定性 (σ²_motion)
    """
    predicted_mean = current_mean + motion_change
    predicted_var = current_var + motion_var  # 运动增加了不确定性
    return [predicted_mean, predicted_var]

# ===== 实战模拟 =====
# 模拟数据：传感器读数（有噪声的真实位置）
sensor_readings = [5.0, 6.0, 8.0, 9.0]
# 模拟数据：每一步施加的控制（移动量）
motions_applied = [1.0, 2.0, 2.0, 1.0]

# 噪声参数
sensor_noise = 3.0      # 测量噪声方差，值越大传感器越不准
motion_uncertainty = 2.0 # 运动模型噪声方差，值越大模型越不可靠

# 初始估计：我们完全不知道在哪，所以方差极大
estimated_position = 0.0
position_uncertainty = 500.0

print("=== 开始卡尔曼滤波 ===")
for i in range(len(sensor_readings)):
    print(f"\n--- 第 {i+1} 步 ---")

    # 1. 更新步骤：融合传感器数据
    estimated_position, position_uncertainty = update_belief(
        estimated_position, position_uncertainty,
        sensor_readings[i], sensor_noise
    )
    print(f"更新后: 位置={estimated_position:.2f}, 不确定性={position_uncertainty:.2f}")

    # 2. 预测步骤：根据运动模型预测
    estimated_position, position_uncertainty = predict_state(
        estimated_position, position_uncertainty,
        motions_applied[i], motion_uncertainty
    )
    print(f"预测后: 位置={estimated_position:.2f}, 不确定性={position_uncertainty:.2f}")

# 最终结果
print(f"\n=== 最终估计 ===")
print(f"位置: {estimated_position:.2f} ± {position_uncertainty**0.5:.2f} (标准差)")

运行这段代码，你将看到：尽管初始猜测距离真实值很远（初始为0，真实起点为5），但仅经过几次迭代，估计值就快速收敛到真实轨迹附近，同时不确定性从500骤降至个位数。这就是卡尔曼滤波的核心魅力——在噪声中持续学习与优化。

三、升维思考：从一维到多维状态空间

现实世界的系统状态往往是多维的。例如，一个在平面移动的机器人，其状态至少包含位置(x, y)，若还想估计速度，则状态变为(vx, vy)。此时，一维的标量均值升级为状态向量，标量方差也扩展为协方差矩阵。

关键概念升级：

• 状态是向量：例如 x = [位置x, 位置y, 速度x, 速度y]ᵀ
• 不确定性是矩阵：协方差矩阵 P 不仅记录每个状态分量的方差（不确定度），还记录它们之间的协方差（相关性），例如位置和速度通常是相关的。

多维卡尔曼滤波框架

多维卡尔曼滤波延续了“预测-更新”的循环节奏，但全部用线性代数工具实现：

标准符号说明：

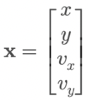
• x：状态估计向量。
• P：状态估计的协方差矩阵。
• F：状态转移矩阵。描述状态如何随时间演变。例如对于匀速运动模型，在一个时间步长 dt 内：

  F = [[1, 0, dt, 0],
       [0, 1, 0, dt],
       [0, 0, 1,  0],
       [0, 0, 0,  1]]

  它将旧状态 [x, y, vx, vy] 映射到新状态 [x+vx*dt, y+vy*dt, vx, vy]。

• H：观测矩阵。它将状态空间映射到测量空间。如果传感器只能测量位置(x,y)，而状态包含位置和速度(x,y,vx,vy)，则：

  H = [[1, 0, 0, 0],
       [0, 1, 0, 0]]

• R：测量噪声协方差矩阵。
• I：单位矩阵。

核心方程（了解架构，代码已封装）

预测步骤：

1. x' = F @ x （基于模型预测新状态）
2. P' = F @ P @ F.T + Q （传播不确定性，Q为过程噪声）

更新步骤：

1. y = z - H @ x （计算残差或创新）
2. S = H @ P @ H.T + R （残差的不确定性）
3. K = P @ H.T @ inv(S) （计算卡尔曼增益）
4. x = x + K @ y （更新状态估计）
5. P = (I - K @ H) @ P （更新协方差，信心提升）

代码实战：二维位置与速度估计

假设我们有一个移动机器人，其GPS传感器只能提供带噪声的(x,y)位置读数，但我们希望同时估计它的速度(vx, vy)。这正是卡尔曼滤波大显身手的场景。

import numpy as np

class KalmanFilter2D:
    """一个简单的2D卡尔曼滤波器，估计位置和速度"""

    def __init__(self, dt=1.0):
        """
        参数:
        dt: 时间步长（秒）
        """
        self.dt = dt

        # 状态向量: [x, y, vx, vy]
        self.x = np.array([[0.], [0.], [0.], [0.]])
        # 状态协方差矩阵 P: 初始时非常不确定
        self.P = np.eye(4) * 1000

        # 状态转移矩阵 F: 恒定速度模型
        self.F = np.array([
            [1, 0, dt, 0],
            [0, 1, 0, dt],
            [0, 0, 1, 0],
            [0, 0, 0, 1]
        ])
        # 观测矩阵 H: 只能观测到位置(x, y)
        self.H = np.array([
            [1, 0, 0, 0],
            [0, 1, 0, 0]
        ])
        # 观测噪声协方差 R
        self.R = np.eye(2) * 1.0
        # 过程噪声协方差 Q
        self.Q = np.eye(4) * 0.01
        self.I = np.eye(4)

    def predict(self):
        """预测步骤：基于运动模型预测下一时刻状态"""
        self.x = self.F @ self.x
        self.P = self.F @ self.P @ self.F.T + self.Q
        return self.x[:2].flatten()  # 返回预测的位置

    def update(self, z):
        """
        更新步骤：用新的测量值修正估计

        参数:
        z: 测量向量 [meas_x, meas_y]
        """
        z = np.array(z).reshape(2, 1)
        # 计算创新（测量残差）
        y = z - self.H @ self.x
        # 创新协方差
        S = self.H @ self.P @ self.H.T + self.R
        # 卡尔曼增益
        K = self.P @ self.H.T @ np.linalg.inv(S)
        # 更新状态估计
        self.x = self.x + K @ y
        # 更新协方差估计
        self.P = (self.I - K @ self.H) @ self.P
        return self.x.flatten()  # 返回更新后的完整状态

# ===== 模拟一个移动物体的轨迹 =====
if __name__ == "__main__":
    # 创建滤波器
    kf = KalmanFilter2D(dt=1.0)

    # 模拟真实轨迹（匀速直线运动）
    true_states = []
    for t in range(10):
        true_x = t * 2.0  # 每秒向右移动2单位
        true_y = t * 1.0  # 每秒向上移动1单位
        true_states.append([true_x, true_y, 2.0, 1.0])

    # 模拟带噪声的测量
    np.random.seed(42)
    measurements = []
    for true_x, true_y, _, _ in true_states:
        # 添加高斯噪声到真实位置
        noisy_x = true_x + np.random.randn() * 1.5
        noisy_y = true_y + np.random.randn() * 1.5
        measurements.append([noisy_x, noisy_y])

    print("=== 2D卡尔曼滤波演示 ===\n")
    print("时间 | 真实位置 | 测量值(噪声) | 卡尔曼估计(位置) | 估计速度")
    print("-" * 70)

    for i in range(len(measurements)):
        # 预测
        pred_pos = kf.predict()
        # 更新（使用带噪声的测量）
        z = measurements[i]
        updated_state = kf.update(z)
        # 打印
        true_x, true_y = true_states[i][0], true_states[i][1]
        meas_x, meas_y = z
        est_x, est_y, est_vx, est_vy = updated_state

        print(f"t={i:2d} | ({true_x:5.1f},{true_y:5.1f}) | "
              f"({meas_x:5.1f},{meas_y:5.1f}) | "
              f"({est_x:5.1f},{est_y:5.1f}) | "
              f"v=({est_vx:4.1f},{est_vy:4.1f})")

    print("\n=== 效果分析 ===")
    print("即使测量值有明显噪声，卡尔曼滤波估计的轨迹依然平滑准确。")
    print("更重要的是：仅凭位置测量，滤波器成功估计出了隐藏的速度状态！")

这段代码的巧妙之处在于：我们只向滤波器输入了带噪声的位置观测，但它通过内部模型，自动推断并输出了相当准确的速度估计。这展示了卡尔曼滤波从间接、有噪观测中推断系统隐藏状态的能力。

下图动态展示了二维卡尔曼滤波器在估计位置和速度时，其不确定性（蓝色椭圆）如何随时间收敛，以及状态分量间的相关性（ρ）。

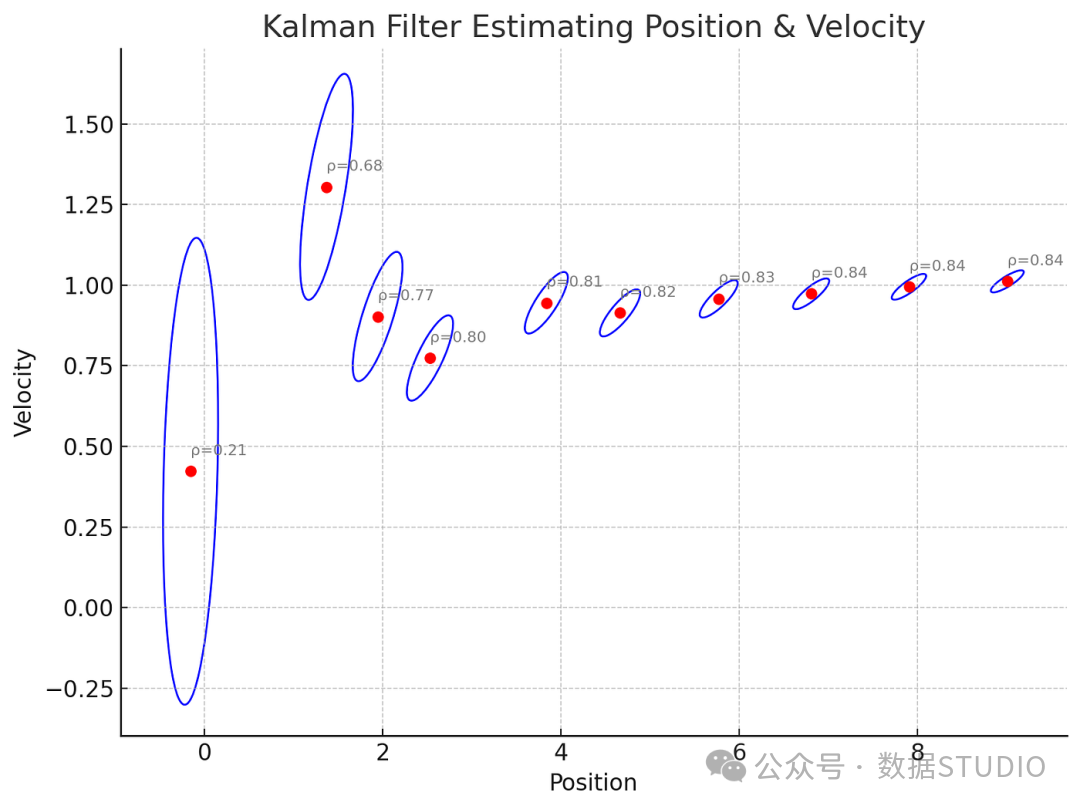
随着滤波迭代：

• 椭圆不断缩小，意味着估计的不确定性随着更多测量数据的融入而减小。
• 相关系数 ρ 趋于稳定，表明系统对位置与速度之间关系的估计越来越有信心。

四、卡尔曼滤波的典型应用领域

自20世纪60年代由Rudolf Kálmán提出以来，该算法已成为工程学众多领域的基石技术，特别是在需要高精度多传感器融合的场景中。例如，在自动驾驶系统中，就需要用它来融合摄像头、毫米波雷达和激光雷达的数据，以构建车辆周围环境的稳定、可靠感知。其他应用还包括：

1. 航空航天：阿波罗登月计划的导航计算机核心算法；现代飞机与卫星的姿态确定与轨道估计。
2. 导航与定位：GPS接收机中，融合卫星信号与惯性测量单元(IMU)数据，提供连续、平滑的位置输出。
3. 机器人学：移动机器人定位(SLAM)、机械臂运动控制。
4. 信号处理：过滤生物电信号（如EEG/ECG）中的噪声，提取有效成分。
5. 经济学与金融：过滤市场价格的短期噪声，尝试识别潜在趋势。

五、核心精髓与进阶方向

卡尔曼滤波的三大精髓：

1. 两步递归：“预测”基于模型推演状态，“更新”用测量修正状态，循环往复。
2. 量化不确定：用协方差矩阵P诚实、精确地表达估计中存在的所有不确定性。
3. 最优融合：通过卡尔曼增益K自动、动态地调整对模型预测和传感器测量的信任权重。

想进一步探索？可以参考以下方向：

• 扩展卡尔曼滤波(EKF)：通过局部线性化处理非线性系统（如涉及旋转的机器人模型）。
• 无迹卡尔曼滤波(UKF)：采用确定性采样（无迹变换）来更优雅地处理非线性，避免求导。
• 粒子滤波(PF)：适用于高度非线性、非高斯甚至多模态的后验分布估计。
• 深入理解其背后的贝叶斯推理和最优估计理论。

结语

卡尔曼滤波器之美，在于它用一个相对简洁、统一的数学框架，优雅地解决了工程中普遍存在的“在噪声与不确定性中寻求最优估计”的难题。它不要求数据绝对干净或模型完全精确，但要求你诚实地量化并管理每一步的不确定性。

通过本文从一维到多维、从原理到Python代码实现的逐步剖析，希望能为你掌握这一强大工具打下坚实基础。