迭代SIC-DFT算法详解：突破OFDM-ISAC中CP限制的原理与性能分析

一体化感知与通信（ISAC）是5G/6G演进中的关键使能技术之一。基于OFDM的波形因其大带宽和高频谱效率，被认为是实现ISAC的理想候选。然而，传统OFDM雷达处理模型通常依赖于一个关键假设：目标的往返传播时延必须完全落在循环前缀（CP）的长度之内。在实际的大距离或高频（如毫米波）通信感知场景中，这一假设往往难以成立，从而引发符号间干扰（ISI）和载波间干扰（ICI），严重恶化感知性能。

系统模型与性能限制

OFDM信号基本参数

考虑一个典型的OFDM-ISAC系统，它使用 N 个子载波和 M 个连续的OFDM符号。

• 总带宽： B = NΔf，其中 Δf 为子载波间隔。
• 符号时长：有效符号时长 T = 1/Δf，添加长度为 T_cp 的循环前缀后，总符号时长为 T_s = T + T_cp。

雷达性能指标与CP约束

• 距离分辨率：由信号总带宽决定，ΔR = c₀ / (2B)，其中 c₀ 为光速。
• CP限制下的最大无干扰距离：为确保时域卷积保持循环特性，目标往返时延需满足 2R/c₀ ≤ T_cp。由此可推导出无ISI的最大感知距离：
  R_max^CP = (c₀ T_cp) / 2
• 多普勒分辨率与无模糊速度：以 T_s 作为脉冲重复周期，观测 M 个符号，速度分辨率为 Δv = c₀ / (2 f_c M T_s)，无模糊速度范围为 |v|_max = c₀ / (4 f_c T_s)。

核心矛盾：RDM（距离-多普勒图）的频域轴理论上能显示由 ΔR 和 N 决定的距离范围，但当时延超出 T_cp 时，物理上必然产生ISI/ICI，导致该距离上的目标回波质量下降。

目标回波与干扰建模

理想情况（CP充分）

假设有 Q 个点目标，其距离、速度、往返时延和多普勒频移分别为 R_q, v_q, τ_q = 2R_q/c₀, f_{d,q} = 2 v_q f_c / c₀。
发射端频域符号矩阵为 S ∈ C^(N×M)。当所有 τ_q ≤ T_cp 时，第 q 个目标的理想频域回波贡献为：
Y_q(n, m) = α_q b_q(n) c_q^*(m) S(n, m)
其中，α_q 是复反射系数，b_q(n) = e^(-j2π n Δf τ_q) 是距离导向矢量，c_q(m) = e^(-j2π f_{d,q} m T_s) 是速度导向矢量。总回波为所有目标贡献的叠加：Y_free = Σ Y_q。

超越CP限制的干扰模型

当存在目标使得 τ_q > T_cp 时，超出CP的时延部分 τ_q^ex = τ_q - T_cp 会破坏循环卷积结构。
此时，完整的频域接收信号模型为：
Y = Y_free + Y_ISI - Y_ICI + Z
其中 Z 是噪声，Y_ISI 和 Y_ICI 分别代表符号间干扰和载波间干扰分量。

干扰的生成涉及一个关键的干扰耦合矩阵 Φ_q。当目标时延完全在CP内时，Φ_q 为零矩阵。当时延超出CP时，Φ_q 的非零元素描述了能量如何在子载波间泄漏：
φ_q(n, n‘) = 1/N Σ_(i=0)^(K_q-1) e^(j2π (n‘-n) i / N)
其中 K_q 是超出CP的离散采样点数。该矩阵精确刻画了“多余时延片段”造成的频域子载波耦合效应。

在复杂的系统建模中，理解此类干扰的数学本质至关重要，这常常需要扎实的网络与系统知识作为基础，以厘清时域与频域之间的映射关系。

距离-多普勒图（RDM）生成

RDM通过二维信号处理将回波映射到距离-速度维度：

1. 频域匹配滤波：利用已知发射符号 S 进行共轭补偿：Ỹ = Y ⊙ S^*。
2. 距离向IFFT：对每个符号的子载波维做 N 点IFFT，将频率索引 n 转换为距离单元 r，对应物理距离 R_r = r · ΔR。
3. 多普勒向FFT：对每个距离单元的符号维做 M 点FFT，将符号索引 m 转换为多普勒单元 k，对应速度 v_k。
4. 幅度谱与归一化：计算每个距离-多普勒单元的功率，并以dB形式显示。

迭代SIC-DFT算法原理

为了克服CP限制，本文提出了迭代干扰抵消方案。其核心思想是，如果能够估计出干扰分量 Y_intf = Y_ISI - Y_ICI，则可以逐步从接收信号中将其减去。

算法流程

在仿真中，我们可以显式获得理想的干扰分量 Y_intf，从而研究算法性能上界。

1. 初始化：Y⁽⁰⁾ = Y（原始接收信号）。
2. 迭代抵消：进行 L 次迭代，第 i 次更新为：
   Y⁽ⁱ⁾ = Y⁽ⁱ⁻¹⁾ - (1/L) Y_intf
   这种渐进式减法有助于稳定收敛过程。
3. 收敛结果：经过 L 次迭代后，理论上 Y⁽ᴸ⁾ ≈ Y_free + Z，即逼近无ISI/ICI的理想回波。

效果对比

下图展示了传统DFT方法与迭代SIC-DFT方法在处理超出CP限制的目标回波时的RDM对比。可以清晰看到，在短CP条件下，传统方法的目标峰值模糊、旁瓣抬高。

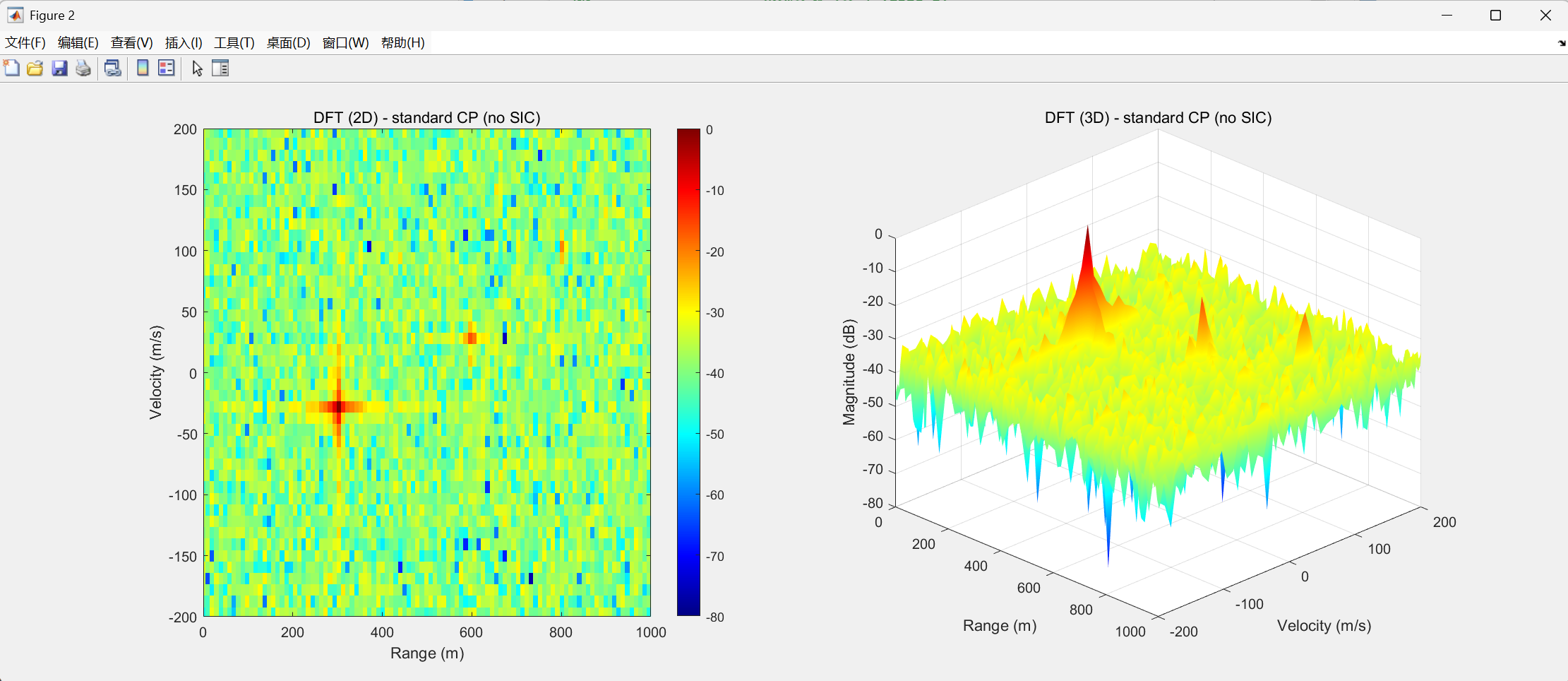
经过5次迭代SIC-DFT处理后，如下图所示，远距离目标的峰值变得尖锐、旁瓣显著降低，证明了该算法在抑制ISI/ICI、提升感知性能方面的巨大潜力。这种通过迭代估计与抵消来优化结果的思想，在算法设计领域具有广泛的适用性。

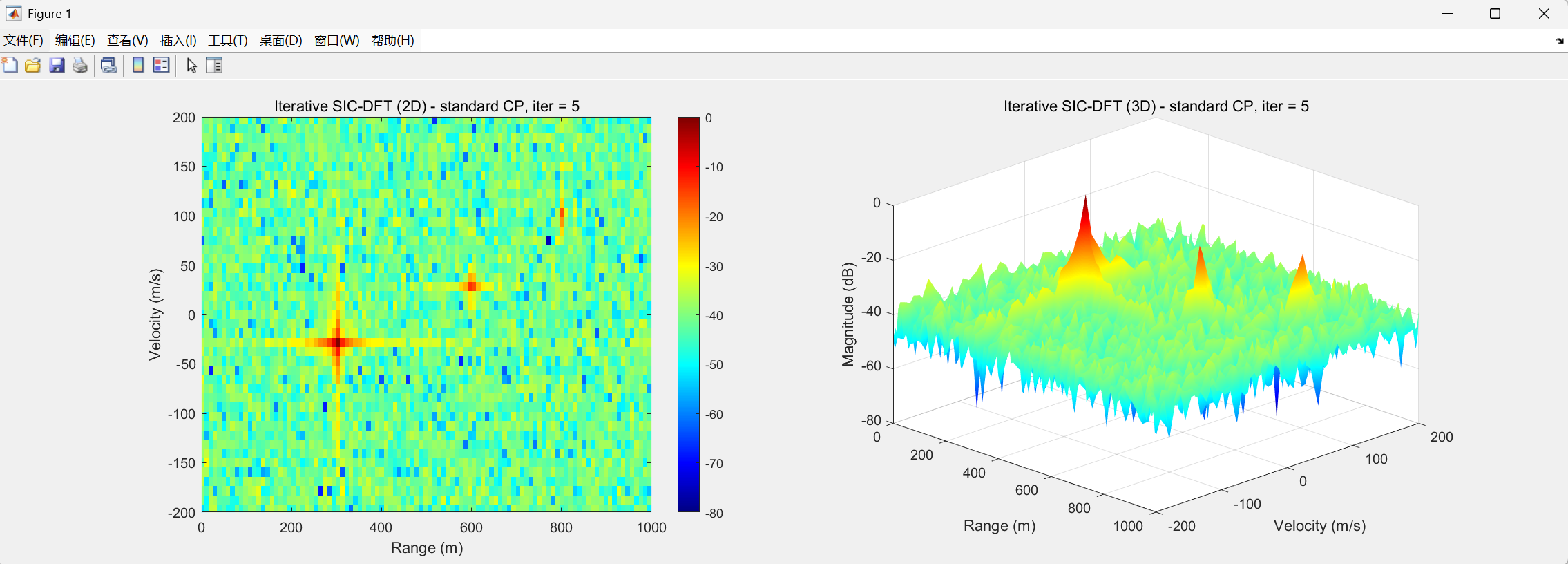
总结与展望

本文系统剖析了OFDM-ISAC系统中因循环前缀（CP）长度不足而引入的干扰问题，并详细推导了迭代SIC-DFT算法的数学原理。通过构建包含ISI/ICI的精确频域模型，并利用干扰耦合矩阵 Φ_q 描述子载波间能量泄漏，该算法能够在频域逐步抵消干扰，从而在标准通信CP设置下，显著扩展有效的雷达感知距离。

从工程角度看，直接增加CP会牺牲频谱效率。本文阐述的“超越CP限制+迭代频域SIC”范式，为在不修改现有通信波形的前提下，提升一体化系统的感知性能提供了理论可行的人工智能与信号处理解决方案，对推动6G ISAC技术的实际部署具有重要意义。