如何为CIC滤波器设计补偿FIR以校正通带滚降

在高性能数字信号处理系统中，CIC（级联积分梳状）滤波器因其高效的抽取/插值能力而备受青睐。然而，它并非完美的“全能选手”——一个显著的缺点在于其通带边缘会产生幅度下降，这种现象被称为通带滚降（Passband Droop）。

为了让目标频带（例如0.1Hz）内的信号幅度保持精准，我们通常需要在CIC滤波器之后级联一个“补偿FIR滤波器”，其核心任务就是将CIC衰减的幅度“拉平”。

CIC通带滚降的数学本质

从数学原理上看，CIC滤波器本质是一个多级移动平均滤波器。其频率响应可以近似用一个sinc函数的N次幂来表示：

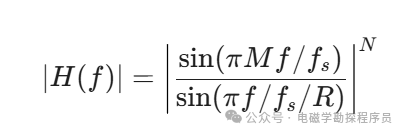
其中，f 代表频率。当频率从0开始增加时，sinc函数（即 sin(x)/x ）的形状并非平坦，而是像一座“山坡”，从顶峰开始逐渐下降。

• 低频区（如0.01Hz附近）：由于频率极低，信号位于sinc函数的顶点附近，因此几乎没有衰减。
• 通带边缘区（接近0.1Hz）：随着频率接近目标截止频率，sinc函数开始明显向下弯曲。对于一个3级（N=3）的CIC滤波器，在通带边缘的衰减可能达到1dB到3dB甚至更多。

可以这样直观理解：CIC就像一个带有弧形的放大镜，中心区域成像清晰，但越靠近镜片边缘，图像就会被“拉伸”并“变暗”。如果不进行校正，测量到的信号强度（例如电磁场信号）就会比真实值偏小。

逆sinc补偿：FIR滤波器的使命

为了“拉平”CIC的频率响应曲线，我们需要在其后串联一个FIR（有限脉冲响应）滤波器。这个FIR滤波器的设计目标非常明确——在CIC幅度下降的地方，提供恰好相反的增益进行提升。

这种设计思路被称为 逆sinc补偿（Inverse-Sinc）。例如，如果CIC在某个频点衰减了-2dB，那么补偿FIR滤波器就需要在该频点提供+2dB的增益，两者级联后在该频点的总增益为0dB，从而实现平坦的通带响应。

在FPGA中实现补偿FIR

在FPGA等硬件平台上实现补偿FIR滤波器时，一个关键优势是它通常在CIC完成降采样后的低数据率域运行。例如，经过61倍抽取后，数据率可能降至1Hz。由于此时时钟频率（如50MHz）相对于数据处理需求极其充裕，因此可以用相对较少的逻辑资源（如单个乘法器配合循环）来实现阶数较高、补偿精度细腻的FIR滤波器。

以下是一个补偿FIR滤波器的Verilog模块框架示例，它兼容多通道处理：

module cic_comp_fir #(
    parameter CH_NUM = 6,
    parameter TAP_NUM = 31, // 补偿滤波器通常需要31~63阶
    parameter DATA_W = 32
)(
    input  wire clk,
    input  wire rst_n,
    input  wire signed [31:0] cic_data_in,
    input  wire [2:0]         chan_idx,
    input  wire               vld_in,
    output reg  signed [31:0] data_corrected,
    output reg                vld_out
);
    // 存储补偿系数的ROM (系数由MATLAB或Python生成)
    // 这些系数的特点是：在低频处增益略小，在接近截止频率处增益略大
    wire signed [15:0] rom_coeffs [0:TAP_NUM-1];
    assign rom_coeffs[0] = 16'hFFFD; // 示例系数...

    // 状态存储：每个通道独立的延迟链
    reg signed [31:0] shift_reg [0:CH_NUM*TAP_NUM-1];

    // 核心计算逻辑：乘累加 (MAC)
    // 此时模块运行在高速时钟（如50MHz），但只需处理1Hz速率的数据，时间充裕
    // 可以采用单个乘法器分时复用，循环计算所有抽头的方式以节省资源
    always @(posedge clk) begin
        if (vld_in) begin
            // 1. 将新数据存入对应通道的移位寄存器
            // 2. 启动一个计数器，依次读取系数并执行乘加运算
            // 3. 计算完成后输出校正后的数据 data_corrected
        end
    end
endmodule

补偿滤波器的设计与验证

补偿FIR滤波器的系数通常借助高级数学工具生成。例如在MATLAB中，可以方便地使用 fdesign.decimator 并指定 ‘ciccomp’ 类型来设计：

% 设计参数：R=61， N=3， 目标通带平坦至0.1Hz
d = fdesign.decimator(1， ‘ciccomp’， 1， 3， 61， ‘Fp,Fst,Ap,Ast’， 0.05， 0.4， 0.01， 60);
h = design(d， ‘equiripple’);
coeffs = h.Numerator; % 获取FIR滤波器系数

为了量化评估CIC的滚降程度并可视化补偿效果，我们可以使用Python进行快速分析和仿真。这涉及到对 数字信号处理 基础频率响应概念的理解。

import numpy as np
import matplotlib.pyplot as plt

def cic_response(f， R， N， M=1):
    """
    计算CIC滤波器的频率响应幅度
    f: 频率数组
    R: 抽取倍率 (本例为61)
    N: 级数 (本例为3)
    M: 差分延迟 (通常为1)
    """
    f = np.array(f)
    f[f == 0] = 1e-20  # 防止除以0

    # CIC频率响应公式 (已归一化，DC增益为1)
    # |H(f)| = | sin(pi*M*f) / (R * sin(pi*f/R)) |^N
    numerator = np.sin(np.pi * M * f)
    denominator = R * np.sin(np.pi * f / R)
    mag = np.abs(numerator / denominator)**N
    return mag

# --- 参数设置 ---
R_rate = 61         # 抽取倍率
N_stages = 3        # 级数
fs_in = 61.0        # 输入采样率 (Hz)
fs_out = fs_in / R_rate  # 输出采样率 (1.0 Hz)
target_f = 0.1      # 目标信号频率 (Hz)

# 生成频率轴 (0 到 输出奈奎斯特频率)
f_axis = np.linspace(0， fs_out / 2， 1000)

# 计算CIC响应 (分贝形式)
magnitude = cic_response(f_axis， R_rate， N_stages)
magnitude_db = 20 * np.log10(magnitude)

# 计算目标点0.1Hz处的衰减
mag_target = cic_response(target_f， R_rate， N_stages)
db_target = 20 * np.log10(mag_target)

# --- 绘图 ---
plt.figure(figsize=(10， 6))
plt.plot(f_axis， magnitude_db， label=f'CIC (R={R_rate}， N={N_stages})'， color='blue'， linewidth=2)
plt.axvline(x=target_f， color='red'， linestyle='--'， label=f'Target: {target_f}Hz')
plt.plot(target_f， db_target， ‘ro’)  # 标出目标点

# 添加注解
plt.annotate(f'Loss at {target_f}Hz: {db_target:.4f} dB\n({mag_target*100:.2f}% Amplitude)'， 
             xy=(target_f， db_target)， xytext=(target_f+0.05， db_target+0.5)，
             arrowprops=dict(facecolor='black'， shrink=0.05))

plt.title('CIC Filter Passband Droop (Roll-off)')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude (dB)')
plt.grid(True， which="both"， ls="--"， alpha=0.5)
plt.legend()
plt.ylim([db_target - 2， 0.5])  # 缩放纵轴以便观察
plt.show()

print(f"在 {target_f} Hz 处的幅度损失为: {abs(db_target):.4f} dB")
print(f"这意味着真实幅值被压减到了原来的: {mag_target*100:.2f}%")

补偿带来的价值

1. 幅度精度：补偿能直接提升测量精度。例如，未经补偿时，一个100μV的信号在通过CIC后可能被衰减为95μV。补偿FIR可以校正这一偏差，确保读数的准确性。
2. 相位保持：精心设计的FIR滤波器可以具有线性相位特性，这保证了目标频带（如0.1Hz）的波形在通过整个滤波链路后，不会产生相位失真或时间上的扭曲，这对于需要保持波形形状的应用至关重要。

通过结合数学分析、工具辅助设计和硬件描述语言（如Verilog）实现，开发者能够有效地克服CIC滤波器的固有缺陷，构建出高性能的数字信号处理链。对于更深入的 C/C++ 算法实现或嵌入式系统优化，可以在 云栈社区 找到更多相关的讨论和资源。