Diffie-Hellman与椭圆曲线安全风险及后量子密码算法威胁剖析

本文将继续深入探讨密码学中的安全性问题。由于侧重点在于分析，因此不会对密码学基础概念进行详细阐述。如需理解相关术语，建议参考《密码学原理与实践》、《深入浅出密码学》等经典教材，或阅读《图解密码技术》作为入门。

Diffie-Hellman

迪菲-赫尔曼密钥交换（Diffie–Hellman key exchange， D-H）是一种安全协议，它允许双方在不安全信道中，无需预先共享任何信息即可协商出一个共同的密钥。该密钥可用于后续通信的对称加密。

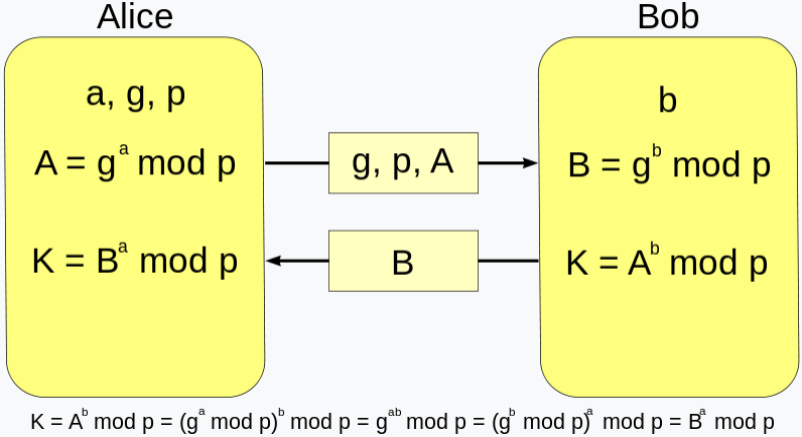
D-H函数

DH协议的核心是DH函数。通信双方从一个乘法群 Zp* 中随机选取私有值 a 和 b。然后计算各自的公共值：
A = g^a mod p
B = g^b mod p

双方交换公共值后，结合自己的私有值进行计算。关键在于，双方计算出的共享秘密是相同的：
A^b = (g^a)^b = g^{ab}
B^a = (g^b)^a = g^{ba} = g^{ab}

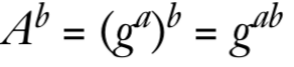
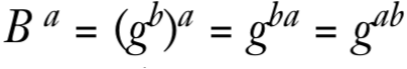
得到的 g^{ab} 称为共享秘密，需传递给密钥派生函数（KDF）以生成最终的对称密钥。

看似简单，实则暗藏玄机。并非任意素数 p 或基数 g 都安全。例如，某些 g 会导致共享秘密的取值范围被限制在一个很小的子集内，而理想情况下，我们希望其取值范围与整个 Zp* 群一样大。

一个安全的要求是：p 应满足 (p-1)/2 也是素数，这可以确保该群不存在会使DH更容易被攻破的更小子群。

D-H问题

在使用DH时，我们不仅关心离散对数问题（DLP），更关注两个特定于DH的问题：计算性Diffie-Hellman问题（CDH）和决策性Diffie-Hellman问题（DDH）。

CDH

计算性Diffie-Hellman问题（CDH）是指：在已知 g^a 和 g^b，但不知道 a 或 b 的情况下，计算出 g^{ab}。

这个问题的意义在于确保攻击者即使截获了双方的公共值，也无法得知共享秘密。如果能解决DLP，自然能解决CDH；但解决CDH不一定能解决DLP。事实上，目前解决CDH的最快方法正是使用数域筛选法（NFS）来求解DLP。关于此类密码学基础难题的深入探讨，可以参考相关资源。

DDH

决策性Diffie-Hellman问题（DDH）是一个比CDH更强的安全假设。它考虑的是，攻击者能否将共享秘密 g^{ab} 与一个随机的群元素区分开来。

设想一个场景：给定公共值和一个可能是 g^{ab} 或随机群元素 c 的值，要求判断哪个是真正的共享秘密。如果DDH是困难的，那么攻击者就无法获得关于 g^{ab} 的任何有效信息。如果能解决CDH，自然能解决DDH，因为一旦计算出 g^{ab}，区分它就轻而易举了。因此，DDH不如CDH难，但它是密码学中被研究最深入的假设之一。

共享秘密用作密钥

通信双方完成DH交换后，得到的是共享秘密 g^{ab}。这里有一个关键点：它本身不是密钥，而是用于派生会话密钥的输入。

密钥应该是随机的比特串，每个比特为0或1的概率应大致相等。但 g^{ab} 是一个群元素，将其编码为比特串后，未必满足这种随机性。

举例说明：考虑乘法群 Z13 = {1,2,...,12}，生成元 g=2。虽然 g^i 可以等概率地生成 Z13 中的所有元素，但将这些元素编码为4比特字符串时，最高位为0的概率是7/12 ≈ 0.58，而不是理想的0.5。因此，直接使用未经处理的共享秘密作为密钥是不安全的。

不安全的群参数

使用不安全的DH群参数会带来严重风险，CVE-2016-0701（OpenSSL漏洞）就是一个典型例子。

给定素数 p，DH操作在其乘法群 Zp 中进行。Zp 可能包含较小的子群。如果在加密协议中使用的大群里存在小子群，那么共享秘密的值域就会被限制在一个较小的集合内，安全性大大降低。更危险的是，攻击者可以精心构造DH指数，在与受害者的公钥结合后，可能逐步泄露甚至完全恢复出受害者的私钥。

椭圆曲线

曲线选择

椭圆曲线密码学的安全性依赖于所选曲线的阶（点的数量）、点的加法公式以及参数的选择。并非所有椭圆曲线都适用于加密，在选择曲线方程 y^2 = x^3 + ax + b 的系数 a 和 b 时，需满足特定要求：

1. 曲线的阶不应等于若干小素数的乘积，否则椭圆曲线离散对数问题（ECDLP）会变得容易求解。
2. 点的加法公式应力求统一。如果攻击者能够区分“点加自身”和“点加不同点”这两种操作，可能会泄露信息。对所有点都使用同一套公式的曲线会更安全。
3. 曲线参数的选择应有公开、合理的解释。如果设计者不说明选择 a、b 的原因，这些参数可能隐藏了弱点。

常用曲线主要包括NIST曲线和Curve25519。

NIST曲线

NIST推荐了多条在素数域上定义的曲线，其中P-256最为常用。它对一个特定的256位素数 p 进行模运算：
p = 2^256 - 2^224 + 2^192 + 2^96 - 1

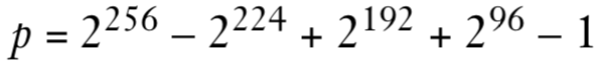
其曲线方程为：
y^2 = x^3 - 3x + b

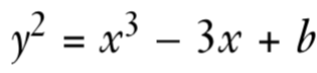
然而，NIST曲线的系数由NSA选定，且未完全公开其选择理由，这引发了一些关于其安全性的讨论和顾虑。

Curve25519

Curve25519由Daniel J. Bernstein设计，被认为是当前最高水平的椭圆曲线Diffie-Hellman函数之一，广泛应用于Chrome、OpenSSH等软件中。它提供约128位的安全强度，其方程形式为：
y^2 = x^3 + 486662x^2 + x

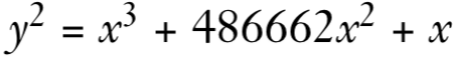
其中，486662是满足作者所设定安全准则的最小整数。这种透明、可验证的参数选择方式增强了人们对它的信任。

随机性差

相较于传统DH，椭圆曲线密码学涉及的参数更多，因此更容易因参数误用而遭受攻击。

以ECDSA签名过程为例，计算 s = (h + r*d) / k mod n 时，需要使用一个秘密随机数 k。如果相同的 k 被重复用于对两个不同的消息进行签名，攻击者就能通过两个签名值恢复出 k，进而推算出私钥 d。

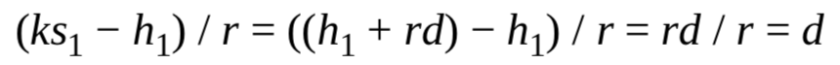
无效曲线攻击

椭圆曲线点加法公式通常只依赖于点的坐标和曲线方程中的 a 系数，而与 b 系数无关。这可能导致“无效曲线攻击”。

假设Alice和Bob正在进行ECDH，并约定使用曲线E和基点G。如果Alice不发送自己在该曲线上的公钥 dAG，而是发送了另一条仅b系数不同的曲线E‘上的一个点P，且P的阶数很小（例如存在小整数k使得kP = O）。Bob在不知情的情况下，会使用自己的私钥 dB 计算共享秘密 dB*P。

由于P在E‘上，且阶数小，dB*P 的结果会被限制在一个很小的取值集合内。攻击者（Alice）在知道P的阶的情况下，可以轻易地枚举出所有可能的共享秘密，从而破坏会话安全性。CVE-2019-9836（SEV固件漏洞）就是一个实际案例。

后量子密码学

量子加速

当一个问题在量子计算机上比在经典计算机上求解更快时，就发生了量子加速。例如，在无序列表中搜索特定项，经典算法平均需要 O(n) 次操作，而量子算法可达到 O(√n)，这是二次加速。

更具颠覆性的是指数加速：经典算法需要指数时间 O(2^n) 的问题，量子算法可能只需多项式时间 O(n^k)。在密码学中，指数时间通常被视为“不可行”，而多项式时间则是“可行”的。

Simon问题展示了指数加速：给定一个满足特定条件的函数 f，经典算法需要约 2^(n/2) 次查询，而量子算法仅需 O(n) 次。

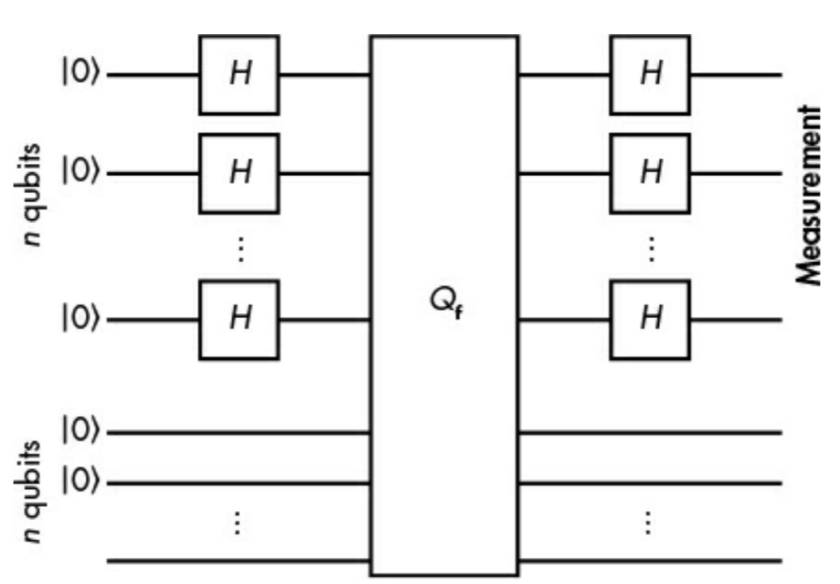
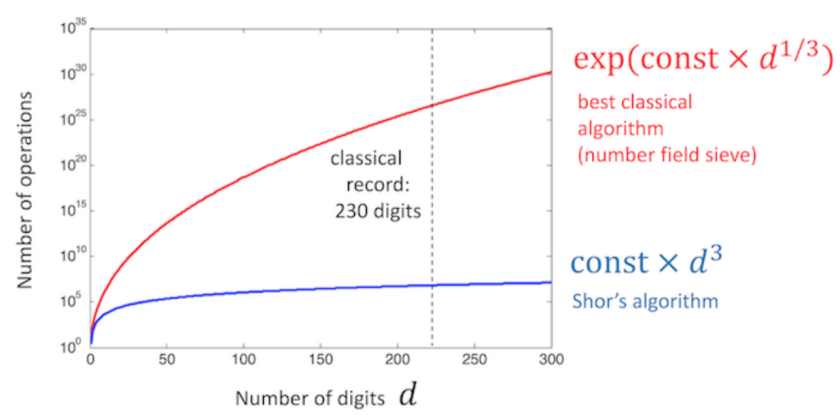
Shor算法

Shor算法能对因式分解、离散对数、椭圆曲线离散对数等问题实现指数加速，直接威胁到RSA、D-H和ECC等广泛使用的公钥密码体制。

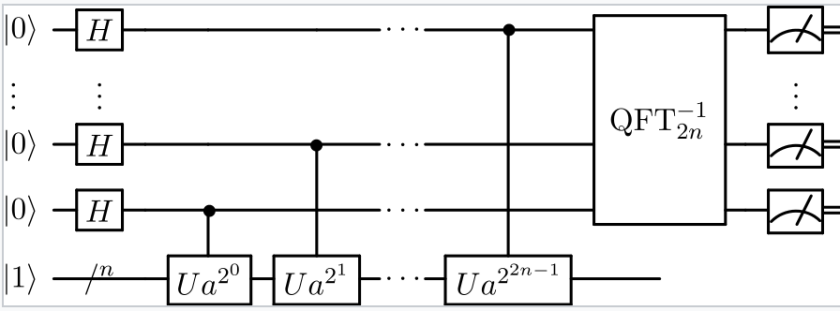
Shor算法本质上是高效寻找周期函数的周期。这种能力可以转化为对公钥密码的攻击。

因式分解

设要分解的大数为 N = p * q。随机选择一个小于N的整数 a，并定义函数 f(x) = a^x mod N。Shor算法可以找到这个函数的周期 ω。找到周期后，可以推导出：
a^ω ≡ 1 (mod N)

这意味着 a^ω - 1 是 N 的倍数。进一步分解：
a^ω - 1 = (a^(ω/2) - 1)(a^(ω/2) + 1)

通过计算 gcd(a^(ω/2) - 1, N) 或 gcd(a^(ω/2) + 1, N)，就有很大概率得到 N 的一个非平凡因子，从而攻破RSA。

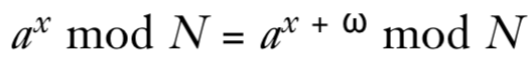
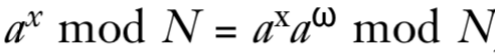
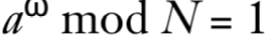
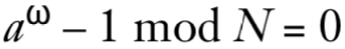
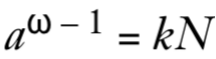
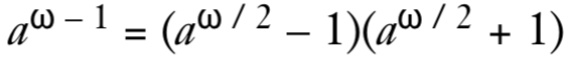
经典的大数分解算法（如数域筛选法）时间复杂度是指数级的，而Shor算法是多项式级的 O(n^2 (log n)(log log n))。

离散对数

对于离散对数问题 y = g^x mod p，可以定义双变量函数 f(a, b) = g^a y^b mod p。利用Shor算法找到该函数的周期 (ω, ω‘)，可以推导出关系：
ω + x ω‘ ≡ 0 (mod q)   （其中q是群的阶）
从而解出 x = -ω / ω‘ mod q。其算法复杂度同样为多项式级。

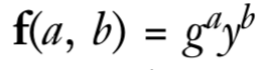
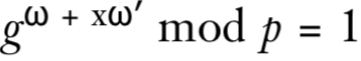
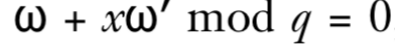
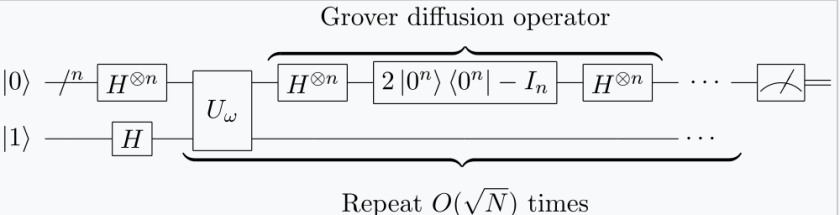
Grover算法

Grover算法提供了二次加速，能在 O(√n) 时间内从n个无序元素中搜索到目标。在密码学中，这意味着：

• 对密钥空间为 K 的对称密码进行暴力破解，时间复杂度从 O(K) 降为 O(√K)。例如，攻击AES-128的理论复杂度从 2^128 降至 2^64。
• 对输出长度为 n 的哈希函数进行原像攻击，时间复杂度从 O(2^n) 降为 O(2^(n/2))。

后量子密码算法

后量子密码学指能够抵抗量子计算机攻击的密码算法，其安全性不依赖于能被Shor算法等解决的数学难题。当前主要研究方向包括四类：基于哈希的、基于编码的、基于格的、基于多变量的。下图展示了NIST后量子密码标准化竞赛第三轮决赛的算法分类。

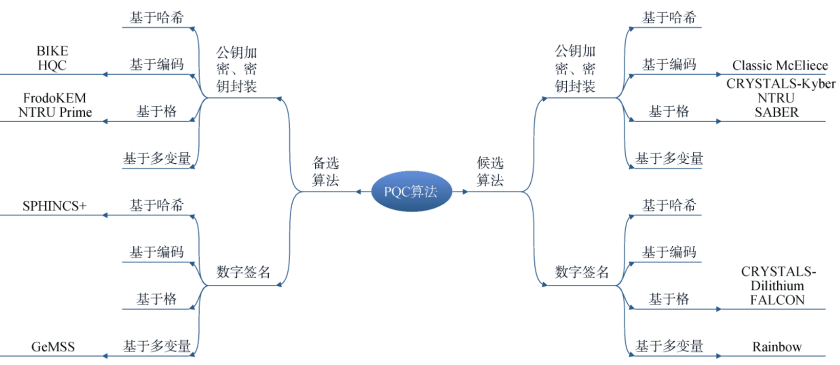
• 基于哈希的签名：安全性源于哈希函数的抗碰撞等性质，典型如Merkle签名方案。
• 基于编码的公钥密码：安全性基于一般线性码的解码问题是NP完全问题这一难题，例如McEliece密码体制。
• 基于格的公钥密码：安全性基于格中的最短向量问题（SVP）、最近向量问题（CVP）或LWE/SIS等NP难问题，是目前最受关注的后量子密码方向之一，涉及复杂的算法设计。
• 基于多变量的公钥密码：安全性基于求解有限域上随机生成的多变量非线性多项式方程组的困难性。

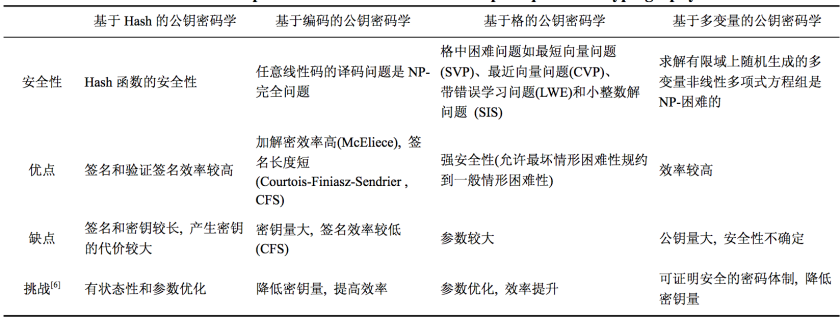
这四类后量子密码算法的横向对比如下表所示：

对密码学及其演进感兴趣的开发者，可以在云栈社区等技术论坛找到更多关于网络安全与前沿技术的讨论资源。

参考

1. https://qrunes-tutorial.readthedocs.io/en/latest/chapters/algorithms/shor_Algorithm.html
2. https://en.wikipedia.org/wiki/Shor%27s_algorithm
3. https://web.archive.org/web/20190702011957/https://seclists.org/fulldisclosure/2019/Jun/46
4. https://csrc.nist.gov/Projects/elliptic-curve-cryptography
5. https://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2016-0701
6. https://en.wikipedia.org/wiki/Computational_Diffie%E2%80%93Hellman_assumption
7. https://en.wikipedia.org/wiki/Decisional_Diffie%E2%80%93Hellman_assumption
8. https://zhuanlan.zhihu.com/p/255171562
9. 《Handbook of Elliptic and Hyperelliptic Curve Cryptography》
10. 《Quantum Computing and Quantum Information》
11. https://arxiv.org/abs/quant-ph/9605043
12. https://docs.microsoft.com/zh-cn/azure/quantum/concepts-grovers
13. 《Serious Cryptography》
14. The Survey of Post-quantum Cryptography Hardware Implementation
15. 《Elliptic Curve Cryptography in Practice》
16. https://link.springer.com/chapter/10.1007/978-3-319-24174-6_21