微分与积分电路原理详解：从RC电路到运放实现与PID控制关联

你是否觉得PID控制遥不可及，很神秘？对其原理感到模糊，只知其然而不知其所以然？本文将从另一个视角切入，探究微分、积分电路的本质，旨在帮助你从根本上理解PID控制（比例、积分、微分）的核心思想。

在深入认识微分、积分电路之前，我们必须先了解一个关键元件：电容。教科书常说“电容的电流超前电压90°”，这到底是什么意思？其物理本质又是什么？

要彻底掌握微分、积分电路乃至PID的控制思路，首先必须吃透电容的工作原理。

电容的本质：电荷的容器

从微观角度看，电容就是一个储存电荷的容器。当电荷流入这个容器时，极板间的电场会随着时间逐渐增强。以图1的RC充电电路为例：

1. 充电初始：电容电压 Uc = 0V，电源电压 Ui 全部加在电阻 R 上，即压差 ΔU = Ur = Ui。此时容器内没有电荷，也就没有电场排斥新流入的电荷，所以充电电流 Ic 最大，容抗最小，电容近似于短路。
2. 充电中期：随着 Uc 上升，电阻上的压差 ΔU = Ui - Uc 开始减小。这个过程建立了电场，容器开始表现出对流入电荷的排斥力，电流 Ic 逐渐减小，容抗逐渐增大。
3. 充电结束：当 Uc = Ui 时，压差 ΔU = Ur = 0V。此时容器内电场最强，以最大排斥力阻止电荷流入，电流 Ic = 0，容抗最大，电容近似于开路。

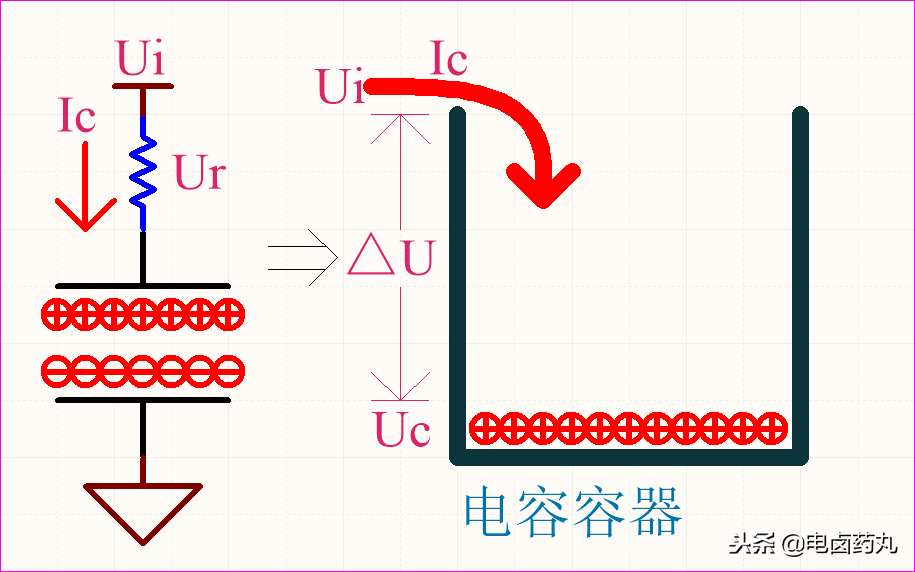
图1：电容充电过程模型

当电荷从容器中流出（放电）时，极板间的电场会随时间逐渐减弱。放电过程中的电容可以看作一个内阻为零的电压源。以图2为例（移除电源并将回路接地）：

1. 放电初始：Uc = Ui，容器充满电荷，电场最强。由于电阻 R 不变，放电电流 Ic 最大（方向与充电相反），电阻两端电压 Ur = Uc = Ui。
2. 放电中期：Uc 下降，电场减弱，放电电流 Ic 随之减小，Ur = Uc 也逐渐减小。
3. 放电结束：Uc = 0V，容器内电荷耗尽，电场消失，Ur = 0V。

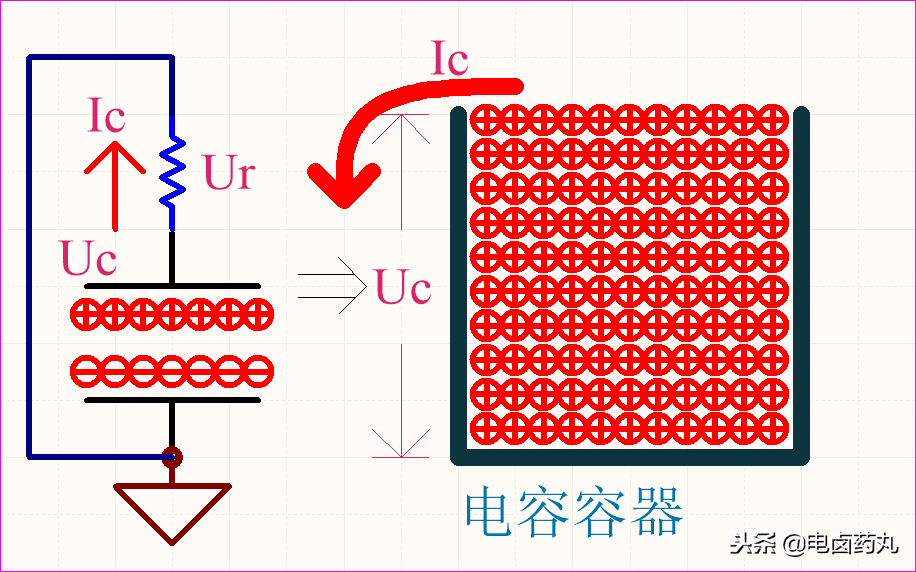
图2：电容放电过程模型（等效为电压源）

电容就像是一个水桶，无论流入的水流是大是小，水位总是从最低处开始连续上升的。电容中电荷的积累也是一个从零开始的连续过程，其积累规律与自然常数 e 相关。图3清晰地展示了电容充放电过程中电压与电流随时间变化的曲线关系。

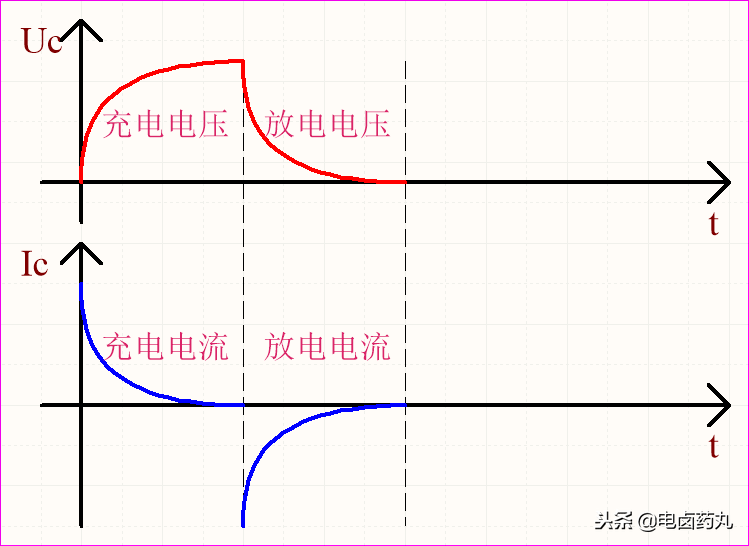
图3：电容充放电过程中的电压-电流曲线

结合以上分析，我们可以总结出电容的几个核心特性：

1. 电容电压不能突变，但电流可以突变（教材公式表述为：电容电流与其两端电压的变化率成正比）。
2. 充电时，电容可等效为一个阻值从极小变到极大的可变电阻；放电时，电容可等效为一个电压逐渐衰减的电压源。
3. 电容电流反映了单位时间内流动的电荷量，而电容电压（或电场）反映了电荷总量的多少。通俗地讲，正是电荷的流动导致了电荷总量的变化（这与特性①吻合）。用数学语言描述，便是“电容的电流超前电压相位90°”。
4. 电容充放电的速度取决于电容 C 和电阻 R 的大小（即时间常数 τ = RC）。

在对电容有了充分了解之后，我们先从最简单的电路开始。

从分压电路到比例(P)、积分(I)、微分(D)的雏形

图4是一个最简单的电阻分压电路，根据欧姆定律，VCC 点的电压为 2.5V。这个纯电阻网络，实际上是比例运算电路的雏形。

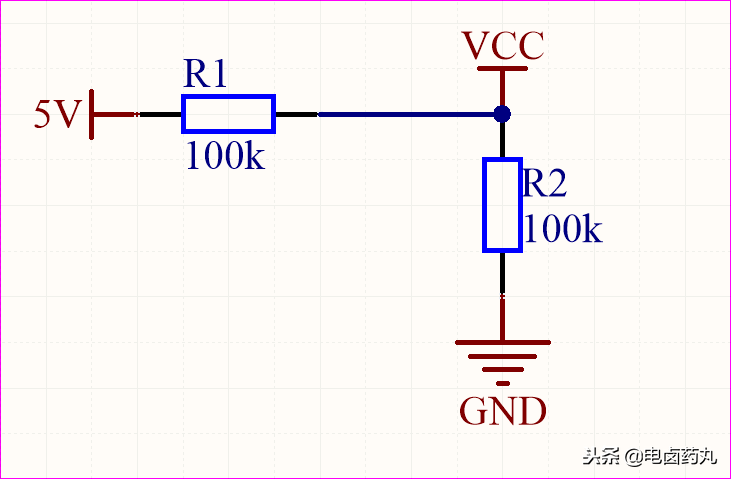
图4：电阻分压电路（比例P的雏形）

如图5，我们将图4中的 R2 替换为一个 0.1μF（104）的电容 C1。根据电容特性，C1 充满电后近似开路，此时 VCC = 5V。这个电路就是积分运算电路的雏形。若将 5V 直流电源换为信号源，它就构成了一个基本的RC低通滤波电路。

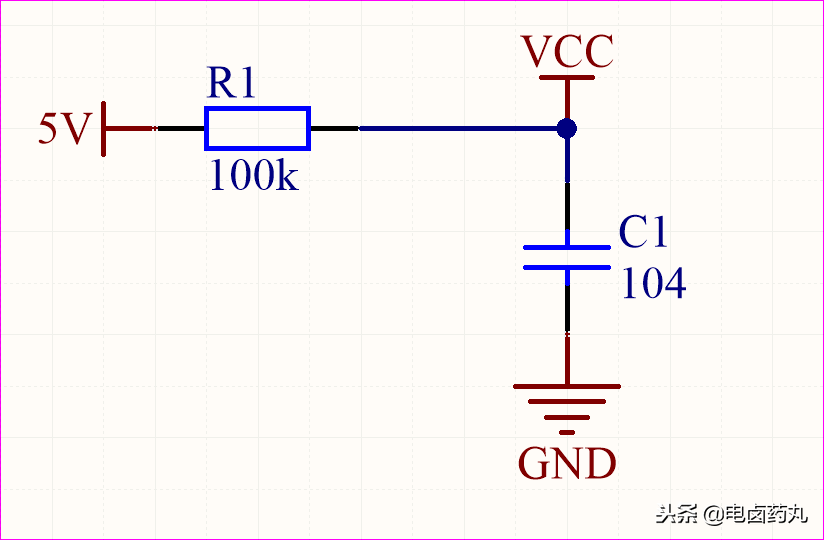
图5：RC积分电路（积分I的雏形）

图6展示了图5电路的充电波形。红色曲线代表 5V 电源（Ui）的波形，蓝色曲线代表 VCC 点的波形。由于电容充电时容抗由小变大直至开路，分压点 VCC 的电压也从 0V 开始缓慢上升，最终达到 5V。电容充电需要时间，导致 VCC 波形变化缓慢，这种波形常见于开关电源的软启动过程。

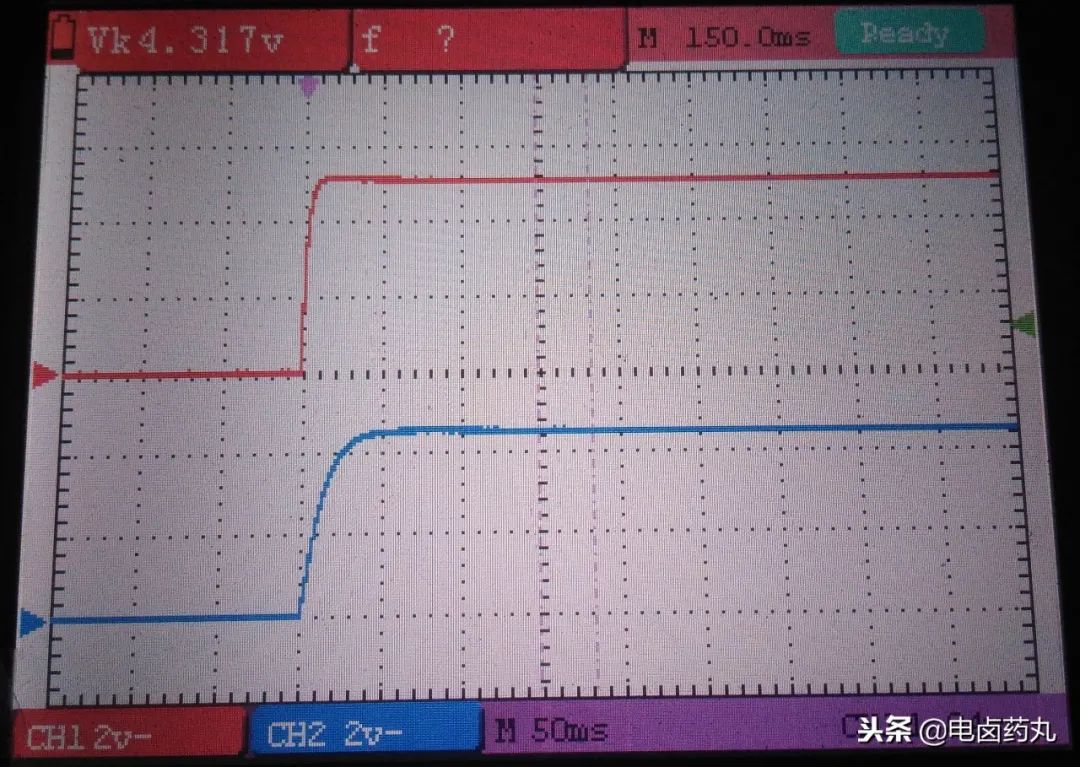
图6：积分电路充电波形

将图4的分压电路和图5的积分电路组合，就得到了图7的电路。这就是我们常用的 PI电路（比例-积分），在基准电压或分压电路中非常常见。加入电容 C1 的目的是引入延时，稳定 VCC 点的电压，使其不受 5V 输入端瞬时波动的影响，最终 VCC 仍稳定在 2.5V。

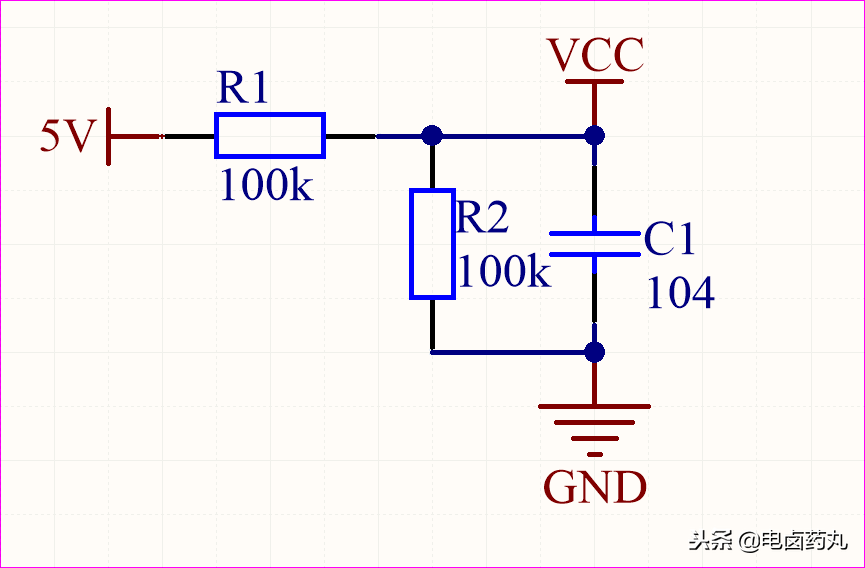
图7：PI电路（比例-积分）

将图5中电阻 R1 和电容 C1 的位置互换，得到图8的电路。C1 充满电后近似开路，此时 VCC = 0V。这个电路就是微分运算电路的雏形。若将 5V 直流电源换为信号源，它就构成了一个基本的RC高通滤波电路。

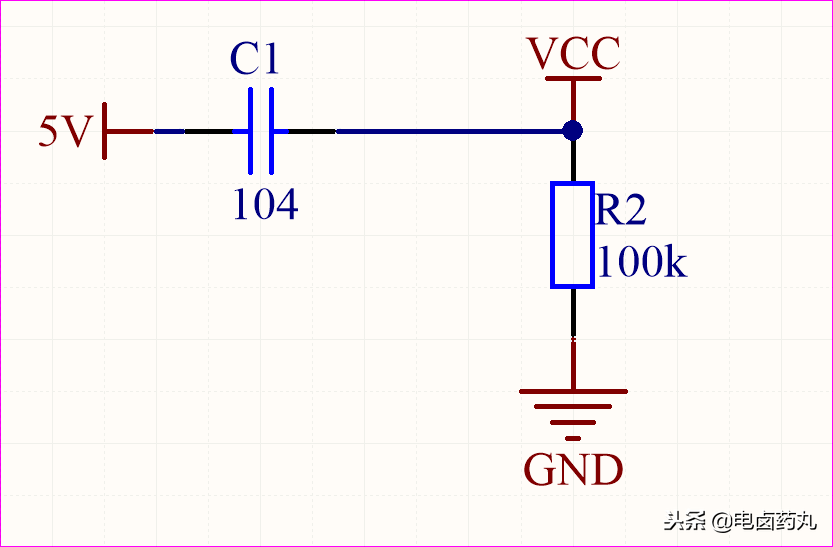
图8：RC微分电路（微分D的雏形）

图9是图8电路的充电波形。红色曲线为 5V 电源（Ui）波形，蓝色曲线为 VCC 点波形。由于电容充电瞬间容抗最小，Ui 从 0V 跳变到 5V 的瞬间，电压几乎全部加在电阻 R2 上，VCC 也瞬间跳变为 5V；随着电容充电，容抗变大，VCC 逐渐下降至 0V。可见，在输入跳变的瞬间，输出 (VCC) 即达到最大值，这体现了 微分“超前预判” 的特性，它反映的是输入信号的变化率。

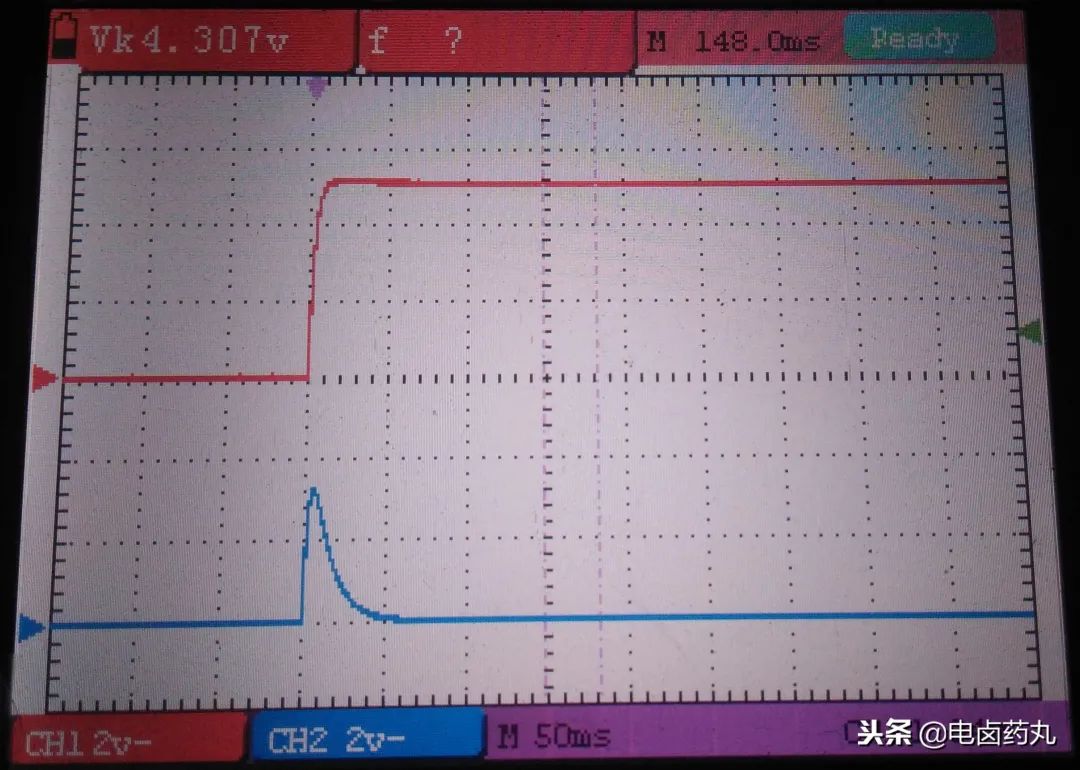
图9：微分电路充电波形

基于运算放大器的微分与积分电路

理解了RC网络的基础，我们再看由运算放大器构成的标准电路。图10是一个反相比例运算电路，其输出电压 Uo 与输入电压 Ui 成固定的比例（线性）关系。关于运放的深入讲解，可参考相关视频。

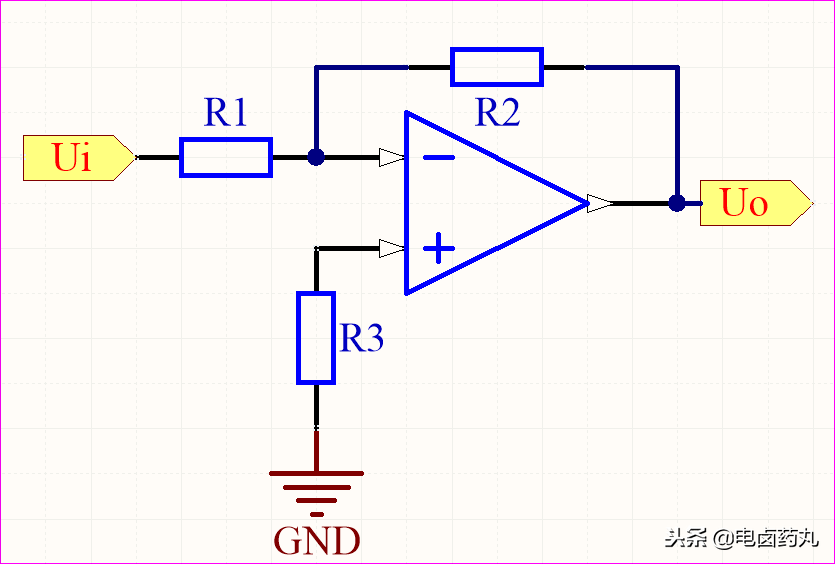
图10：反相比例运算电路

图11展示了比例运算电路的输入输出波形，Uo 与 Ui 相位相反，幅度成比例。

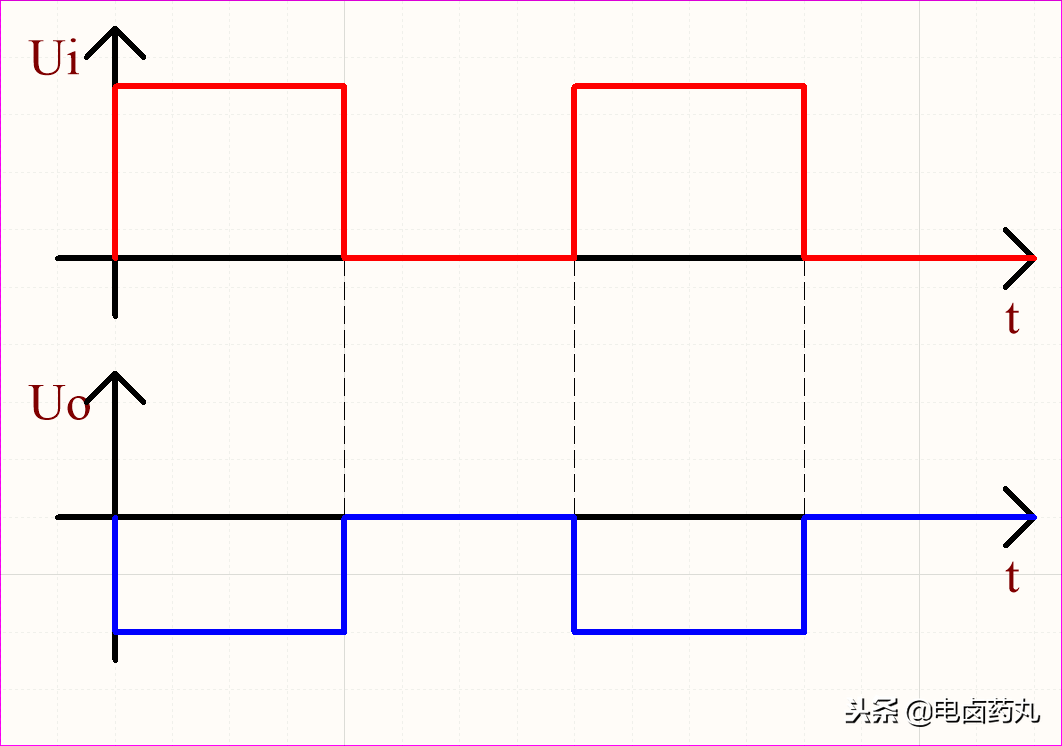
图11：比例运算电路波形

微分运算电路的工作过程

图12和图13展示了微分运算电路的充放电过程：

• 充电过程（图12）：电容 C1 可等效为可变电阻。充电开始时 C1 容抗为0，其两端电压不能突变故为 0V。此时 Ui 全部加在 R1 上，运放反相输入端 (-) 获得正最大峰值电压，导致输出 Uo 为负的最大峰值。随着 C1 充电，其容抗增大，Uo 逐渐回归 0V。
• 放电过程（图13）：电容 C1 可等效为电压源，且电压不能突变。此时放电电流反向最大，在 R1 上产生反向最大压降，运放反相输入端 (-) 获得负最大峰值电压，导致输出 Uo 为正的最大峰值。随着 C1 放电，Uo 逐渐回归 0V。

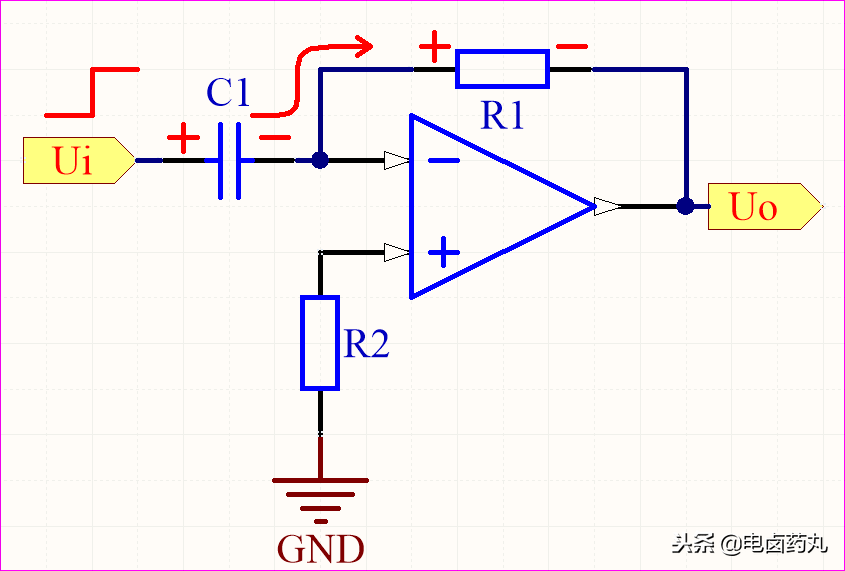
图12：微分运算电路充电过程分析

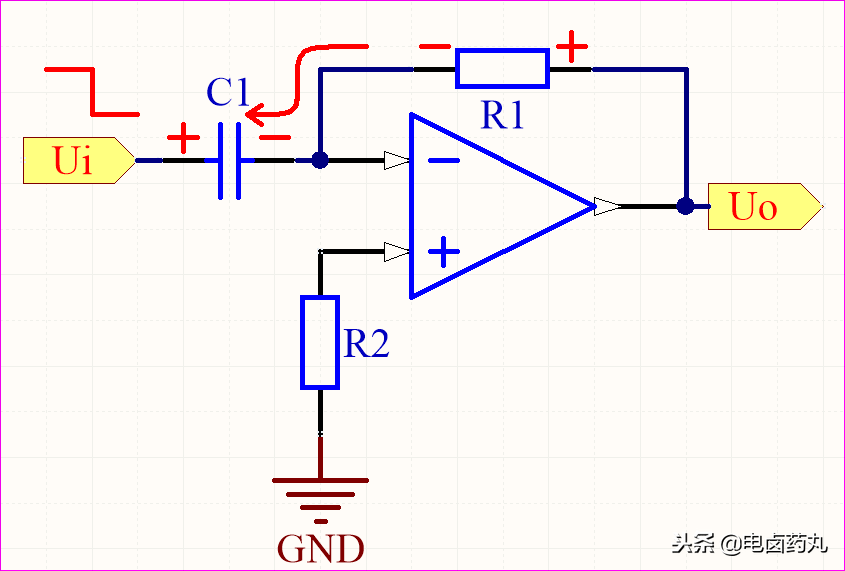
图13：微分运算电路放电过程分析

图14为理想微分运算电路的输入输出波形。结合上述分析可知，输出 Uo 的尖峰脉冲正好对应输入 Ui 的跳变沿，它反映了 Ui 的变化率，实现了“超前预判”的效果。

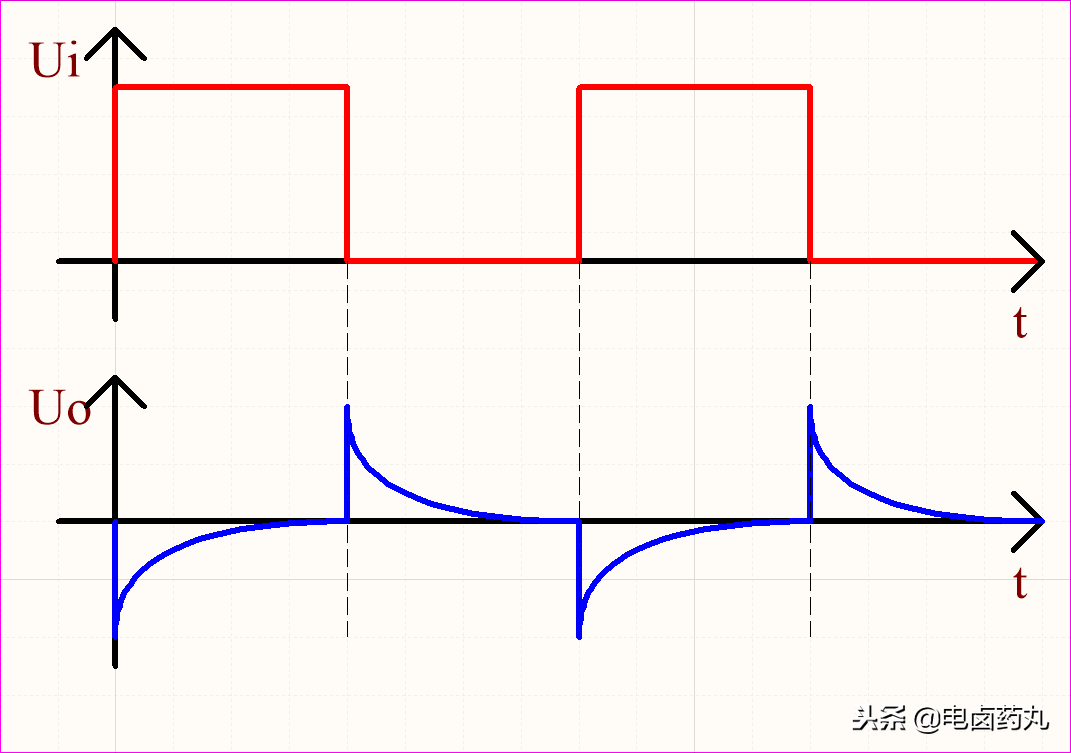
图14：微分运算电路波形

实际微分电路设计

图15是一个更接近实际的微分运算仿真电路。为了防止运放在高频时饱和并抑制噪声，必须在电容 C1 输入端串联一个小电阻 R2。加入 R2 后，电路已不是理想微分电路，但只要输入信号周期大于 2πR1C1，仍可近似实现微分运算。

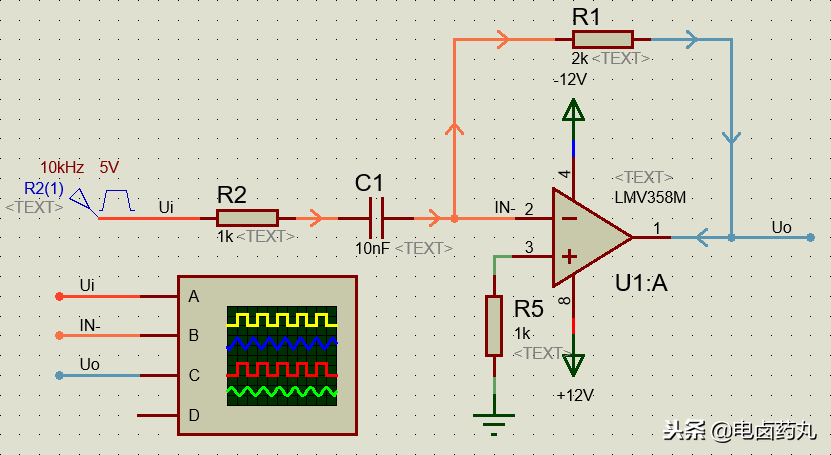
图15：实用微分运算仿真电路（输入端串联电阻R2）

图16是该仿真电路的波形，其中 IN- 是运放反相输入端的波形。

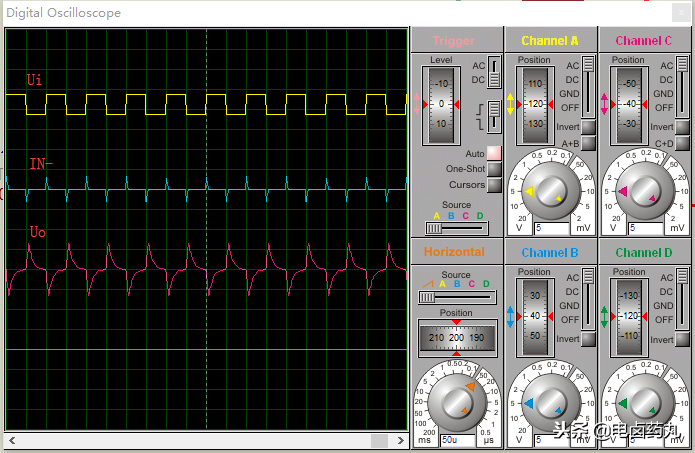
图16：实用微分运算仿真电路波形

积分运算电路的工作过程

图17和图18展示了积分运算电路的充放电过程：

• 充电过程（图17）：电容 C1 可等效为可变电阻。充电开始时容抗为0，其两端电压为 0V，运放反相输入端 (-) 为“虚地”，故输出 Uo 为 0V。随着 C1 被恒定电流（由 Ui/R1 决定）充电，其两端电压线性上升，导致输出 Uo 向负方向线性增长（对于反相积分器），直至达到运放负向饱和值。
• 放电过程（图18）：电容 C1 可等效为电压源。当输入 Ui 变为0或反向时，C1 通过 R1 和运放放电，其储存的电荷量（电压）逐渐减小，输出 Uo 也从负峰值逐渐回归 0V。

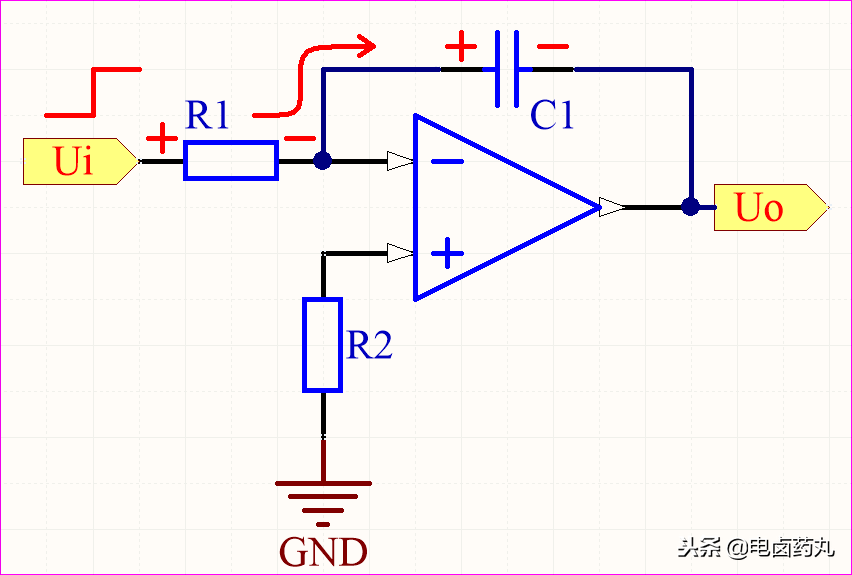
图17：积分运算电路充电过程分析

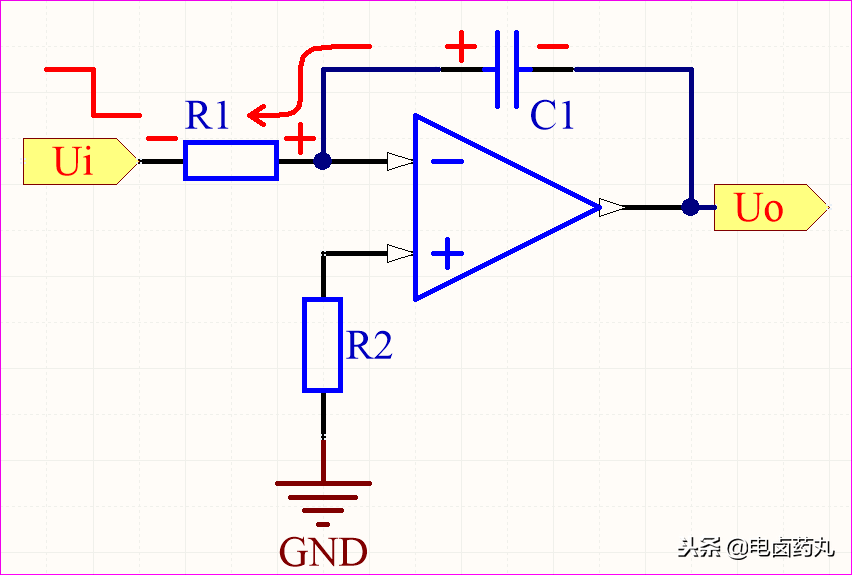
图18：积分运算电路放电过程分析

图19为理想积分运算电路的输入输出波形。输出 Uo 是输入 Ui 的随时间积累（积分）的结果，输入为方波时，输出为三角波，这体现了积分 “延迟稳定” 的效果，能够平滑输入的变化。

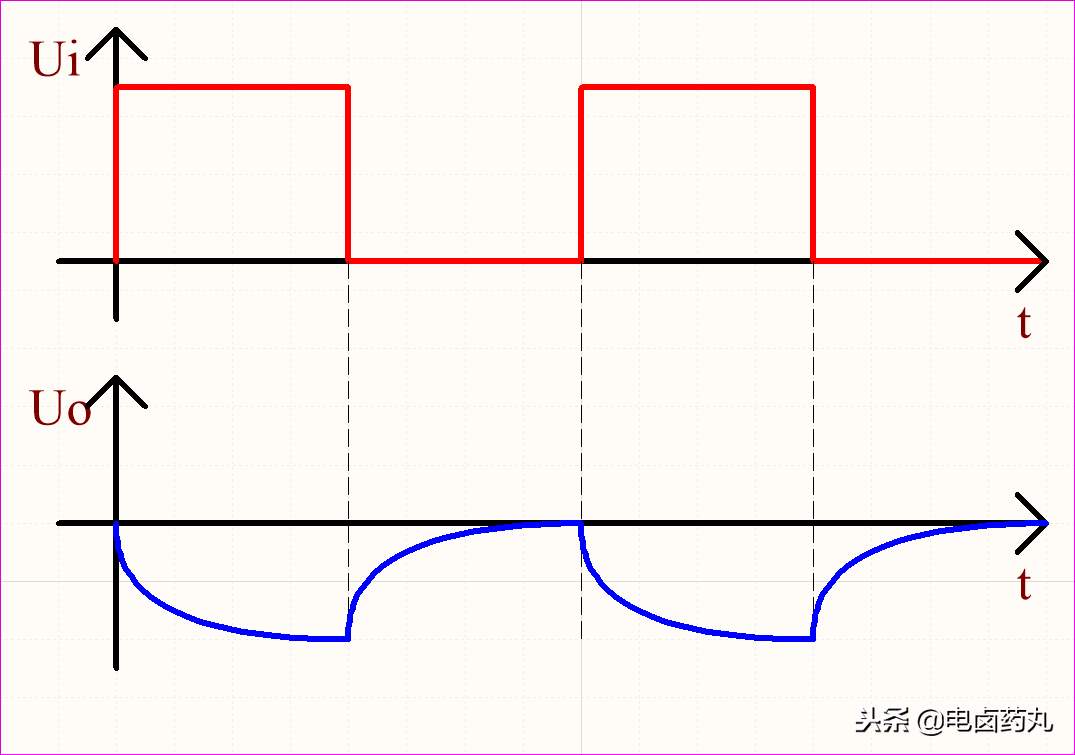
图19：积分运算电路波形

实际积分电路设计

图20是一个更接近实际的积分运算仿真电路。为了防止运放输入失调电压等导致积分结果漂移饱和，通常需要在积分电容 C2 两端并联一个较大的电阻 R3。加入 R3 后，电路已不是理想积分电路，但只要输入信号周期远小于 R3C2，仍可近似实现积分运算。

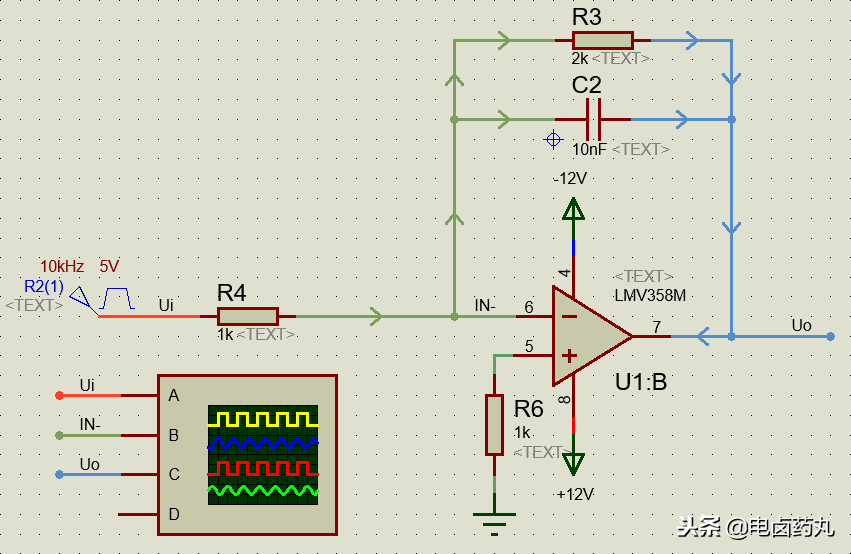
图20：实用积分运算仿真电路（电容并联电阻R3）

图21是该仿真电路的波形，其中 IN- 是运放反相输入端的波形。

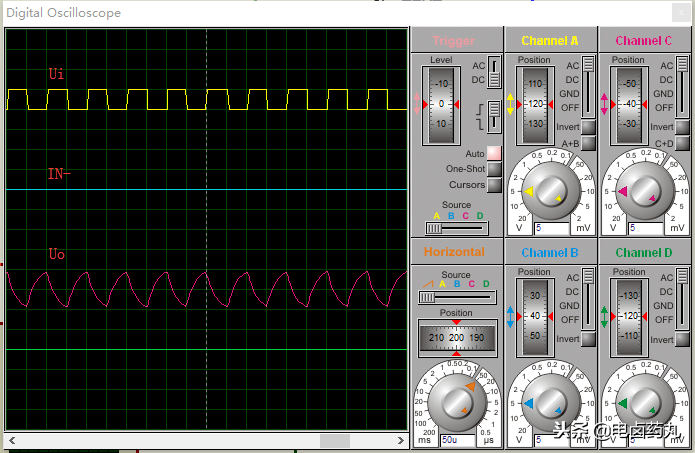
图21：实用积分运算仿真电路波形

核心要点总结

1. 本质：微分与积分运算电路都巧妙地利用了 电容电压不能突变 这一核心特性，通过对输入信号变化率或历史值的响应来调节输出。它们只对变化的输入信号有意义。
2. 特性对比：
   • 微分 (D) 控制 具有 超前预判 的特性，能快速响应系统的变化趋势。
   • 积分 (I) 控制 具有 延迟稳定 的特性，能消除系统的稳态误差。
   • 在PID调节的动态响应速度上：微分 (D) > 比例 (P) > 积分 (I)。

希望本文通过从电容本质到电路雏形，再到运放实现的层层剖析，能帮助你拨开微积分在电路中的应用迷雾，并建立起与PID控制原理的直观联系。理解这些基础模拟电路，是深入掌握自动控制理论的重要一步。如果你想就运放或其他模拟电路话题进行更深入的探讨，欢迎来云栈社区交流分享。