量化策略 | 基于换手率均值捕捉市场注意力的日频因子实现与评价

这个因子是基于异常收益率的注意力捕捉因子的姊妹篇。通常，当看到因子名从“收益率”变为“换手率”时，第一反应是将计算中的所有收益率指标都替换为换手率，这是一种常见思路。

然而，本文讨论的基于换手率的注意力捕捉因子并非如此。它仅仅是将基于异常收益率的注意力捕捉因子时序回归模型中的解释变量——即“行业涨跌停占比/全市场涨跌停占比”——替换成了换手率指标，模型的其他部分保持不变。

关于这个因子的底层逻辑，2025年的《因子日历》给出了如下描述：

不同股票对同一市场关注度事件的反映程度往往是不同的，可借助个股对市场关注度事件的敏感程度来衡量股票对该事件的注意力捕捉效应；捕捉能力越强（敏感程度越高），表明个股更能吸引市场注意，从而导致买盘压力增大，股价高估；该因子以换手率作为市场关注度事件，换手率衡量投资者交易热度，反映关注水平。

计算步骤与代码实现

从理论上讲，计算步骤并不复杂，甚至无需赘述。但由于笔者未见到原始研报，仅依据2025年《因子日历》上的信息进行复现，发现了一个细节：文字描述提及的是“行业中所有标的的平均换手率”，而给出的公式却是“行业中所有标的换手率的标准差”。

因此，在实现时，我计算了两个版本的因子：一个基于换手率的均值 (tr_mu)，另一个基于换手率的波动（标准差，tr_sigma）。

核心代码调整

代码部分的主要改动是将原先计算涨跌停数量的 cal_limit_num 方法替换为计算换手率数据的 cal_tr_data 方法，并在数据加载阶段做了一些精简。

@staticmethod
def cal_tr_data(group):
    group = group.dropna()
    group['tr_mu'] = group['tr'].mean()
    group['tr_sigma'] = group['tr'].std()
    return group[['tr_mu', 'tr_sigma']]

因子评价

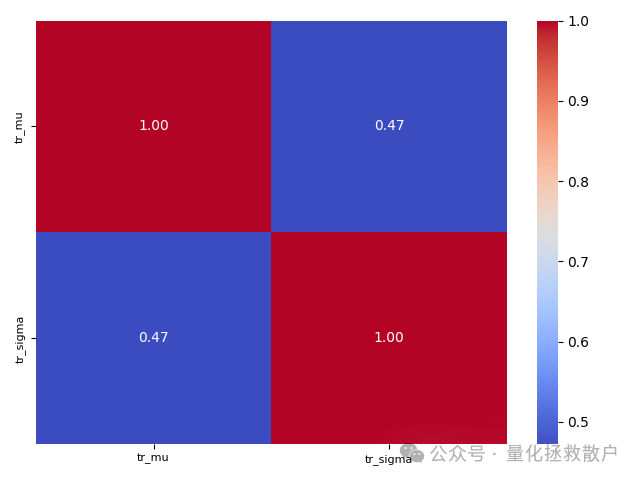
使用换手率均值和标准差计算出的两个因子，它们之间的相关性很低，未超过0.05。从IC（信息系数）表现来看，两者差异不大，但在分层回测中，基于换手率均值计算的因子表现略胜一筹。因此，下文展示的因子评价结果均基于换手率均值版本。

另外需要注意的是，该因子在计算时序回归时已经使用了过去21个交易日的数据进行了平滑，因此通常无需再合成月度因子。当然，理论上可以再进行一次平滑（例如再取21日均值或标准差），但这属于二次平滑，效果未必会提升。实际上，对于本因子，二次平滑会导致效果变差。

IC分析

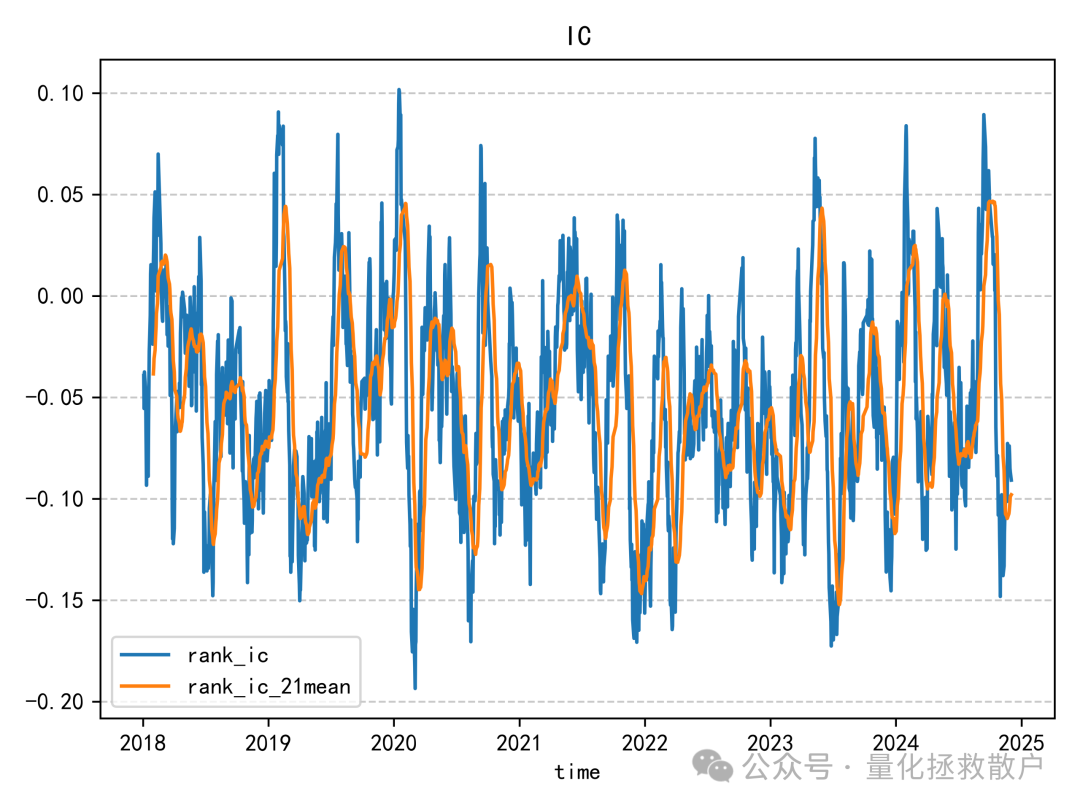
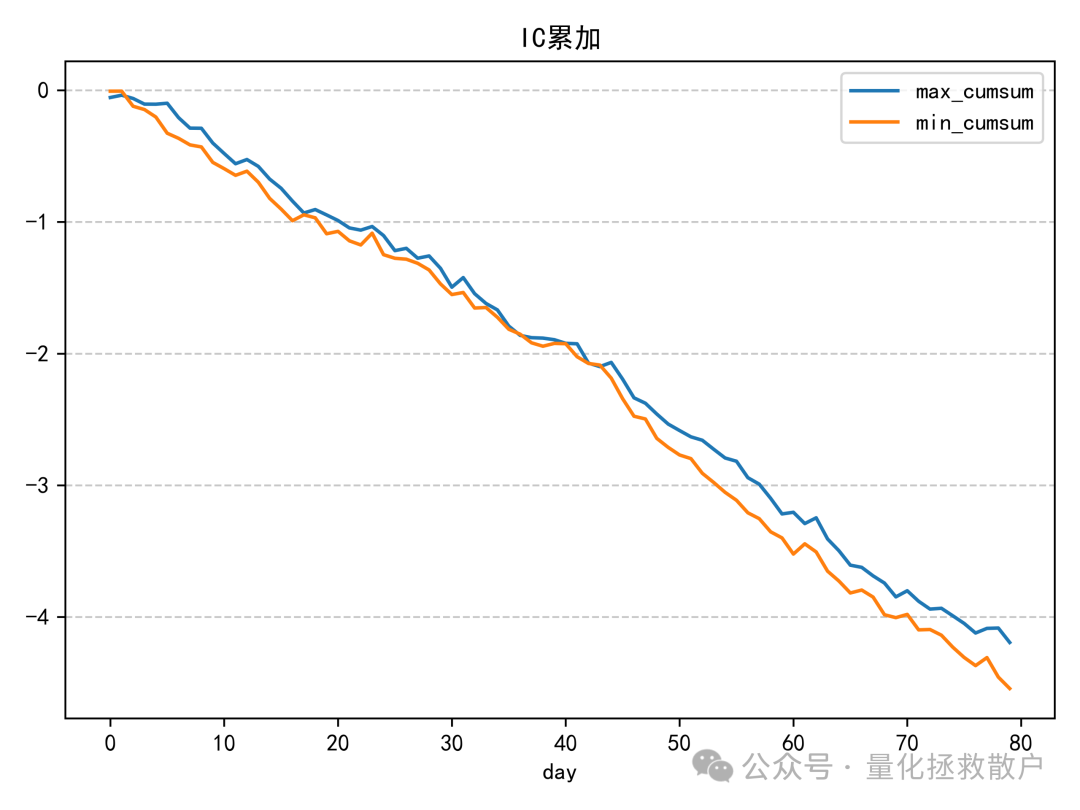
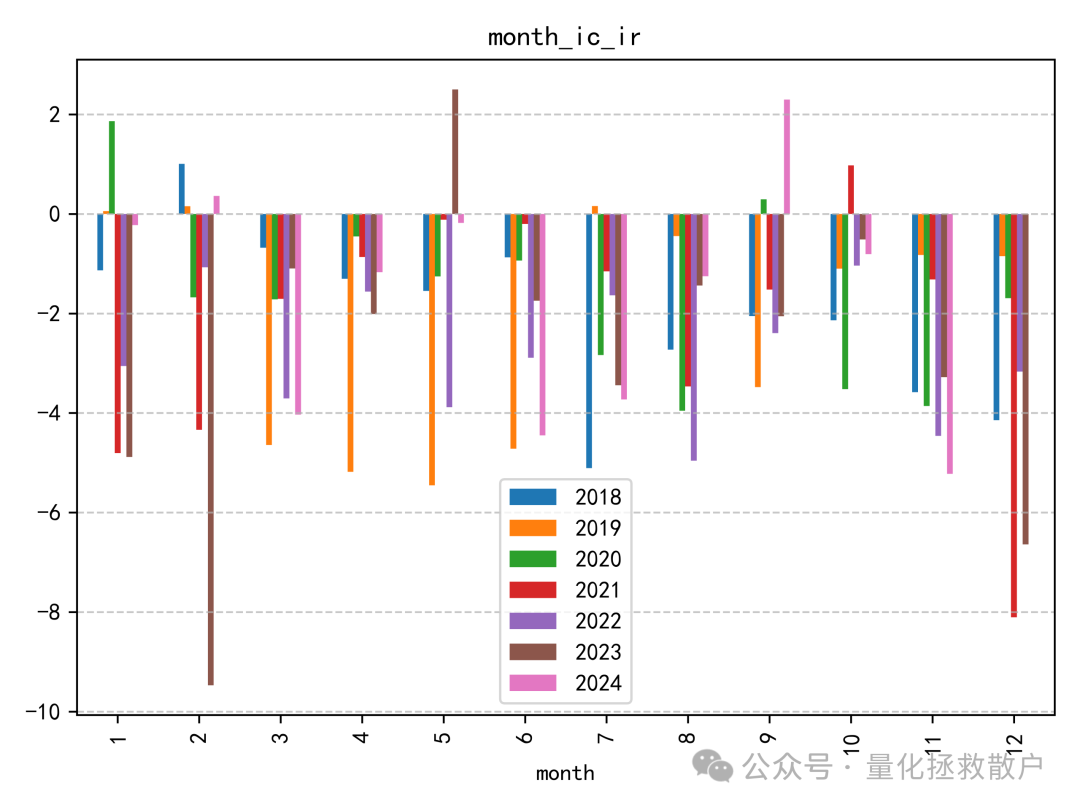
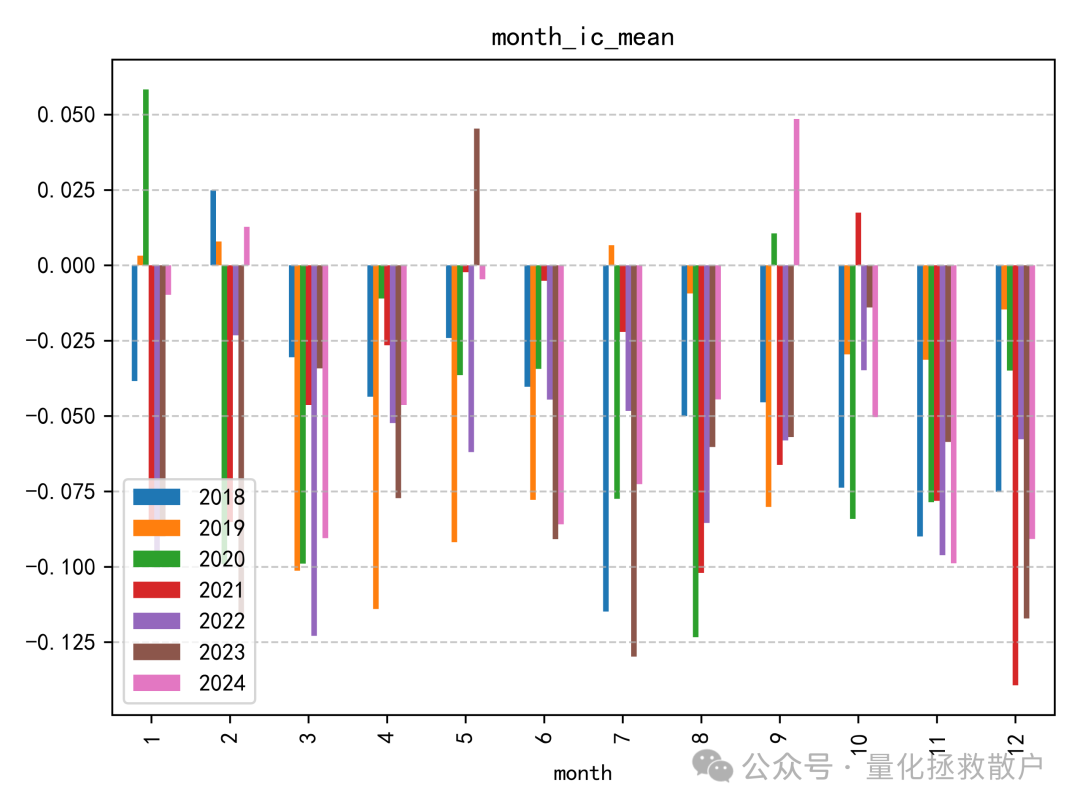
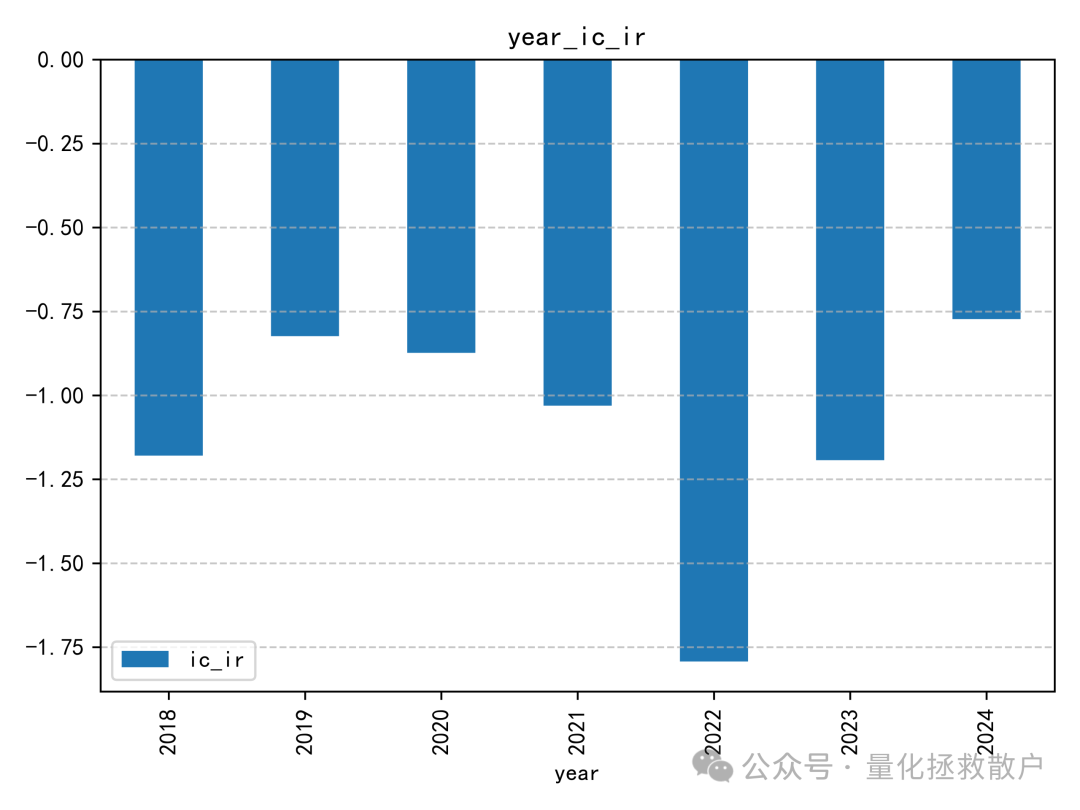
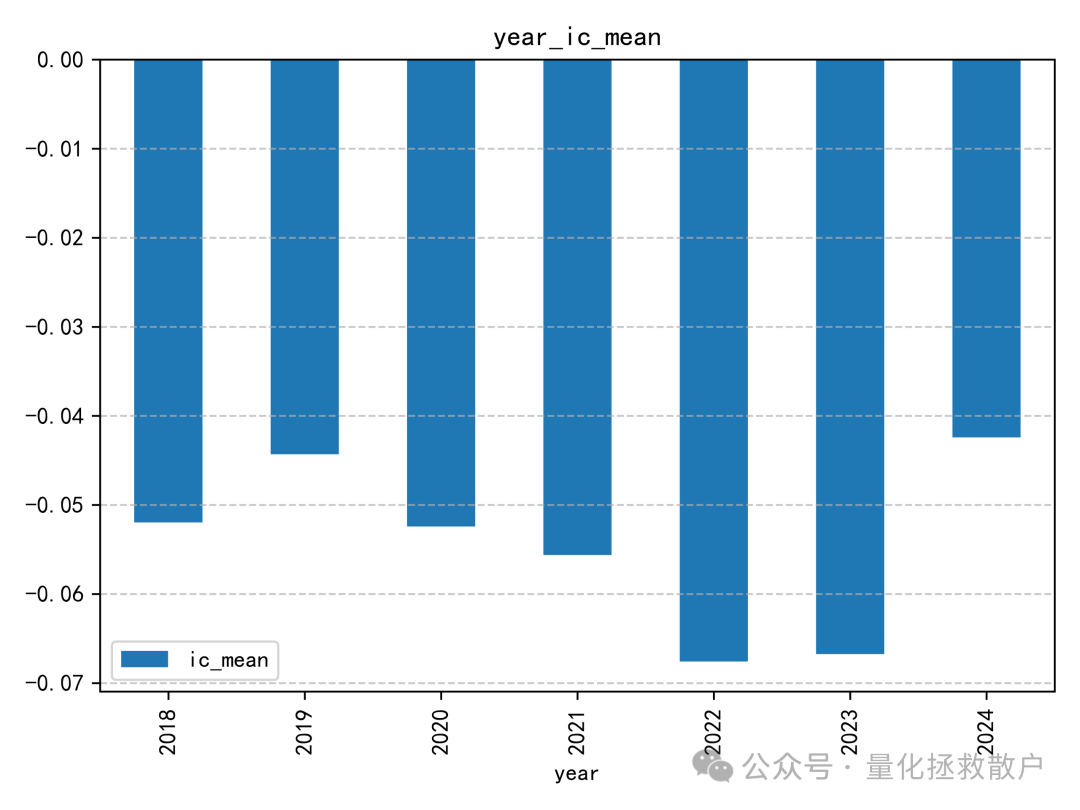
该因子的IC值并不突出，这一点与之前基于异常收益率的注意力捕捉因子情况类似。

回归分析

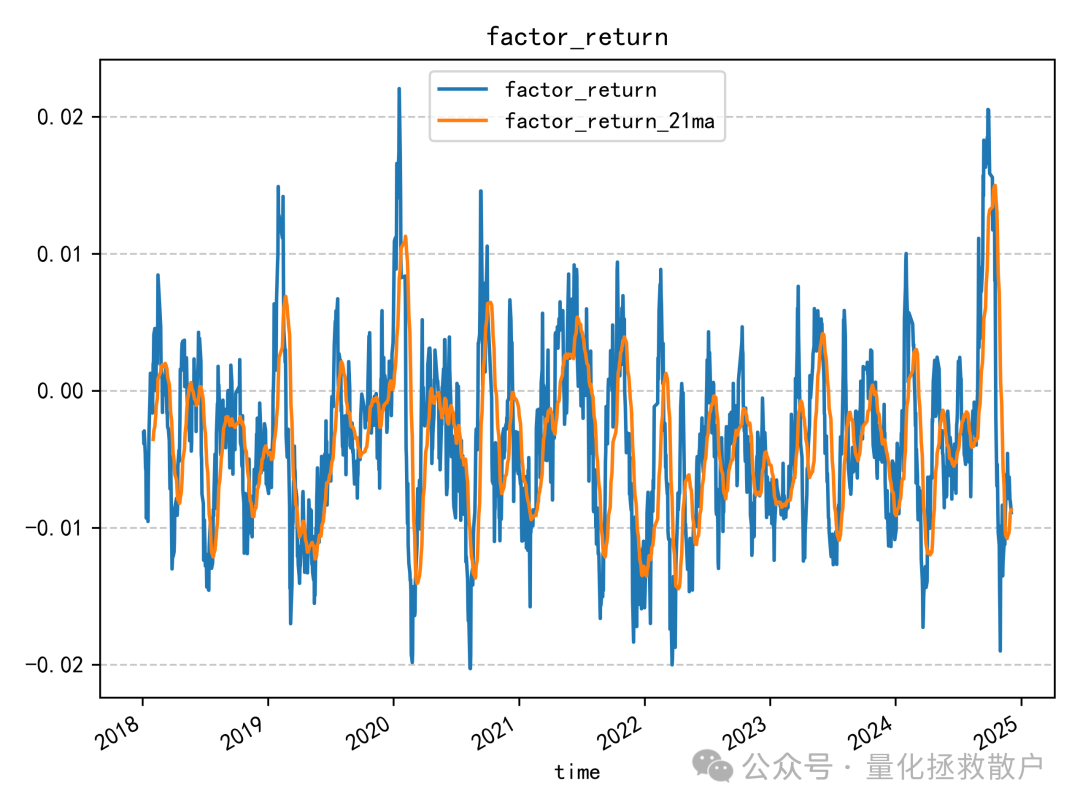
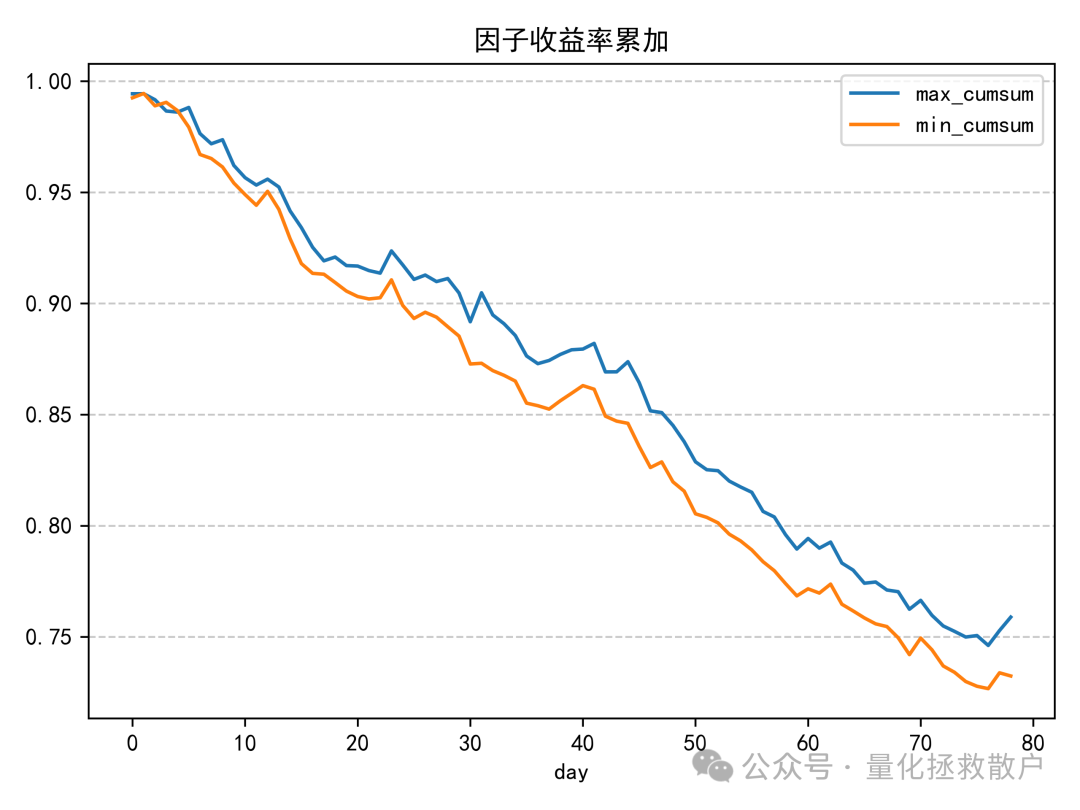
换手率分析

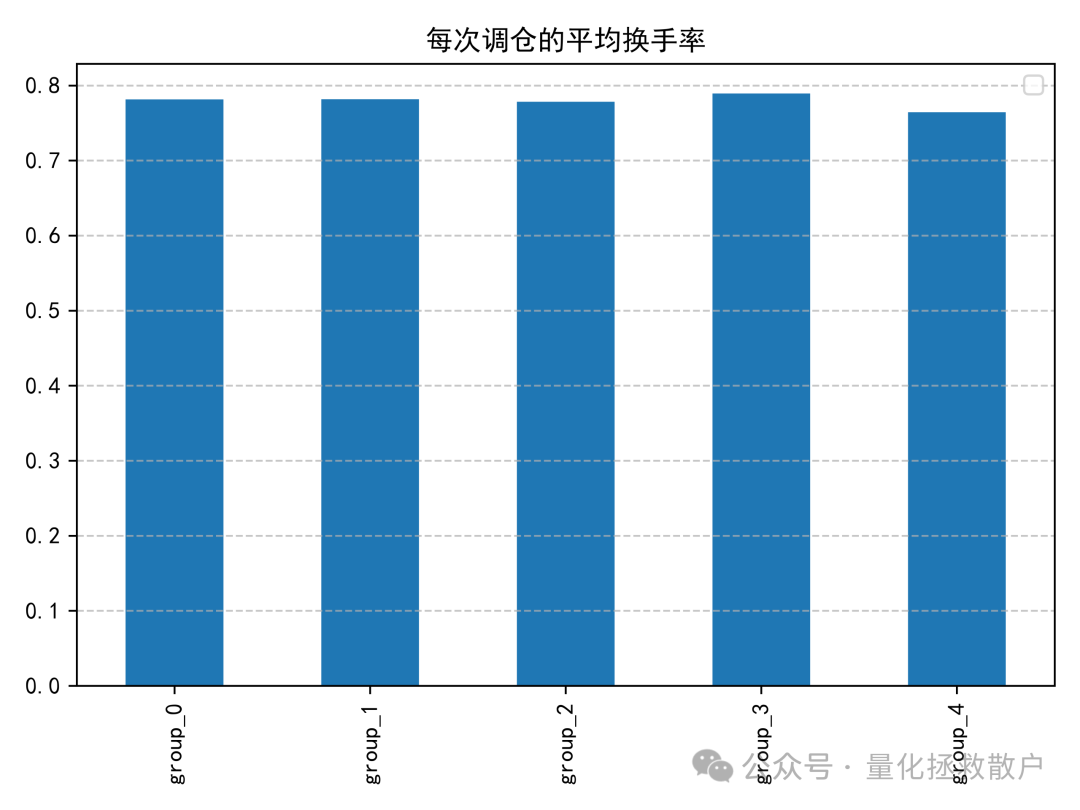
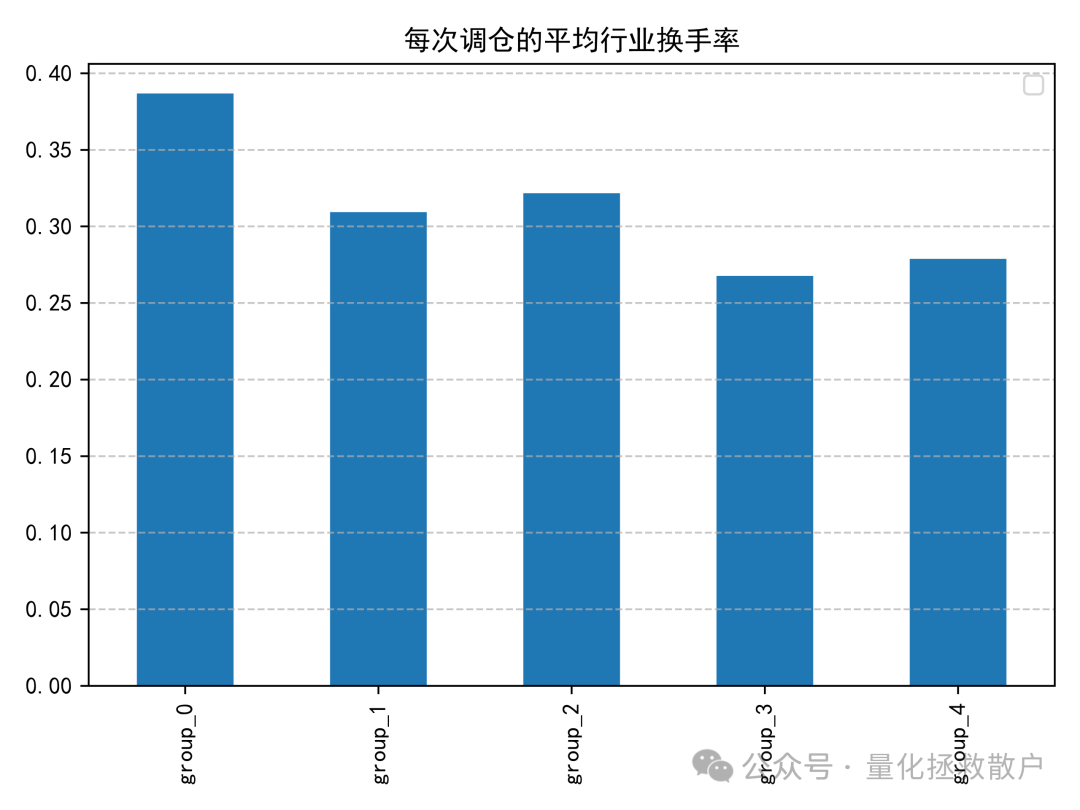
收益分析

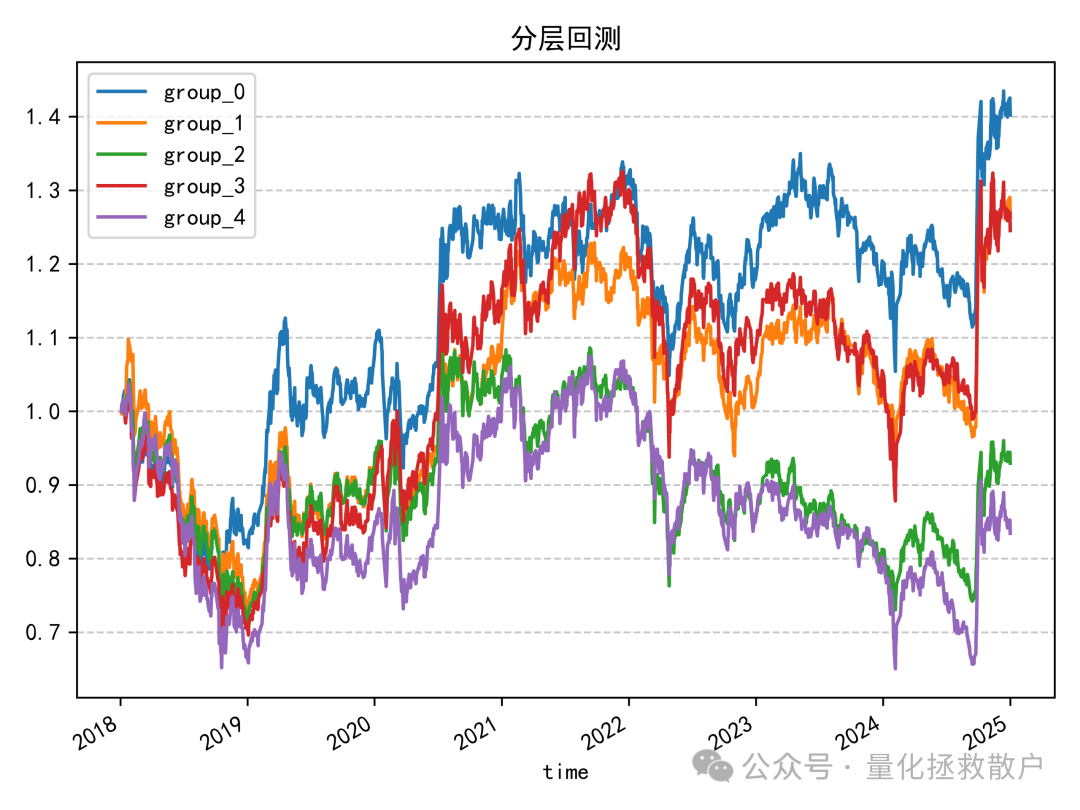
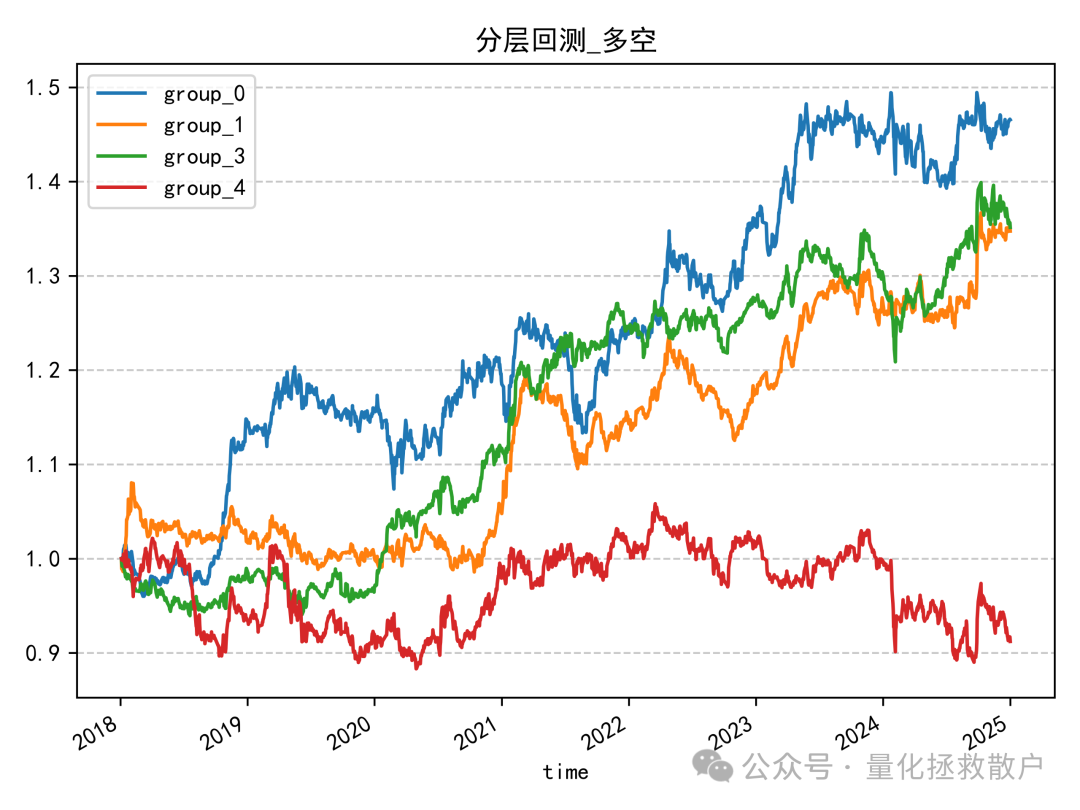
从分层回测结果来看，表现只能说中规中矩。但相比于使用换手率标准差计算的版本，已有明显改善；即使与基于异常收益率的注意力捕捉因子相比，本因子的回测结果也更优。

在复现和测试这个因子的过程中，笔者又萌生了一个“魔改”思路：分别用换手率的均值和中位数计算两个因子，然后做差，看看是否能产生奇效。这类针对因子的深度优化和组合策略，正是量化研究中的有趣之处。不过，这次的“魔改”尝试可能要留到下次再和大家分享了。如果你对量化因子研究和数据处理的实战内容感兴趣，欢迎持续关注云栈社区的相关技术讨论。