算法技巧：快慢指针如何解决链表与数组问题

关于该模式

与双指针模式类似，快慢指针模式也使用两个指针，但区别在于它们会以不同的速度遍历可迭代的数据结构。这种模式的核心用途，通常是识别结构中的循环或查找某个特定目标（比如中点）。根据具体问题的不同，指针的“速度差”是可以灵活调整的。

• 区别：经典的双指针模式侧重于比较数据值，例如在有序数组中寻找和为目标值的两个元素。
• 用途：快慢指针方法则通常用于分析数据的结构或属性本身，比如链表是否有环。

关键思想

算法的核心思想很简单：两个指针从同一个起点出发，然后以不同的“步幅”移动。最常见的设定是，慢指针一次移动一步，而快指针一次移动两步。由于这种速度差，该模式也常被形象地称为“龟兔赛跑算法”（Tortoise and Hare Algorithm），其中快指针是“兔子”，慢指针是“乌龟”。

如果数据结构中存在循环，这两个指针最终会在遍历过程中相遇。这种方法使得算法能够高效地检测出数据结构中的特定属性，例如循环是否存在、中点位置在哪，或者两个序列的交点。

形象化理解：
想象一下两个人在一个圆形跑道上从同一点开始跑步，一个跑得快，一个跑得慢。因为跑道是环形的，跑得快的人最终一定会从后面追上跑得慢的人。这个场景完美地说明了快慢指针如何用于检测循环。

伪代码模板

下面是一个基础的伪代码模板，你可以根据自己遇到的具体问题进行调整和填充：

FUNCTION fastAndSlow(dataStructure):
  # initialize pointers (or indices)
  fastPointer = dataStructure.start   # or 0 if the data structure is an array
  slowPointer = dataStructure.start   # or 0 if the data structure is an array

  WHILE fastPointer != null AND fastPointer.next != null: 
    # For arrays: WHILE fastPointer < dataStructure.length AND (fastPointer + 1) < dataStructure.length:

    slowPointer = slowPointer.next
    # For arrays: slowPointer = slowPointer + 1

    fastPointer = fastPointer.next.next
    # For arrays: fastPointer = fastPointer + 2

    IF fastPointer != null AND someCondition(fastPointer, slowPointer):
      # For arrays: use someCondition(dataStructure[fastPointer], dataStructure[slowPointer]) if needed
      handleCondition(fastPointer, slowPointer)
      BREAK

  # process the result
  processResult(slowPointer)
  # For arrays: processResult(slowPointer) might process dataStructure[slowPointer]

代码逻辑解析：

• 速度差异：fastPointer 的移动速度是 slowPointer 的两倍（在链表中是 .next.next，在数组中则是索引 +2）。
• 循环条件：只要快指针没有到达终点（对于链表是 null，对于数组是末尾），循环就继续。
• 结果处理：
  • 检测条件：如果在移动途中，快慢指针满足了某个特定条件（比如相遇了），就会触发 handleCondition 并中断循环。这常用于检测环。
  • 自然结束：如果循环正常结束（快指针走到头），此时 slowPointer 通常正好位于我们想要的中点位置。这常用于解决寻找分位点的问题。

示例

通过下面两个经典问题，你可以更直观地理解快慢指针的应用。

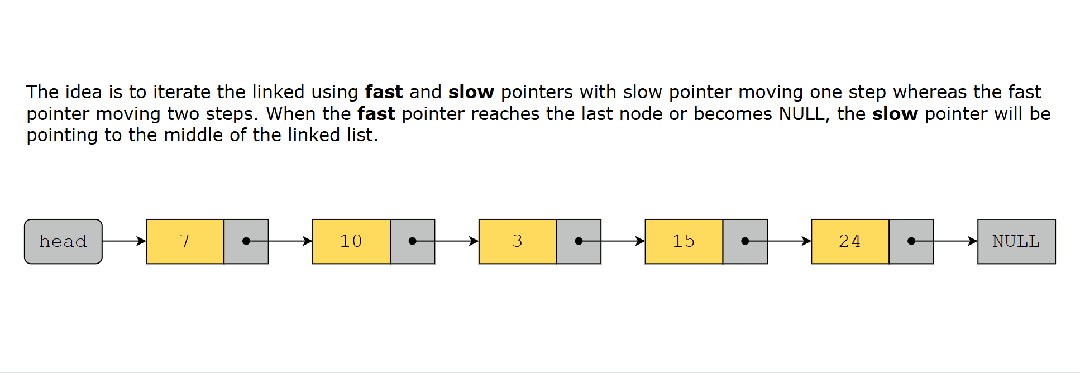
• 链表中间节点 (Middle of the linked list)
  给定一个单链表的头节点，如何高效地返回链表的中间节点？快慢指针是标准解法。

• 数组中检测环 (Detect cycle in an array)
  给定一个由非负整数组成的数组，其中每个元素的值表示下一个元素的索引。判断这个数组中是否存在环（即从某个索引出发，沿着索引指引会无限循环）。

现实世界的问题

快慢指针的思想不仅仅用于解题，在现实世界的软件开发中也能找到它的影子。

• 符号链接验证 (Symlink verification)
  系统管理员需要防止符号链接形成死循环（例如 A 指向 B，B 又指回 A）。

  应用：检查文件链接时，可以用一个指针（“龟”）一次跟随一个链接，另一个指针（“兔”）一次跳跃两个链接。如果两者再次指向同一个文件，就确认存在循环链接，从而避免系统资源被无限消耗。

• 编译面向对象程序 (Compiling OO programs)
  在编译代码时，需要检测模块或类之间的循环依赖（例如 A 依赖 B，B 又依赖 A）。

  应用：编译器可以逐步跟踪依赖关系图。让“龟”指针一次分析一个依赖，“兔”指针一次跳过一个依赖去分析下一个。如果两者在某个模块相遇，就说明存在循环依赖，编译器可以立即报错，提示开发者修复。

何时使用此模式？ (Checklist)

当你遇到一个问题时，可以通过下面这个清单来判断快慢指针是否适用。

必须满足：

1. 线性数据结构：输入数据可以以线性方式遍历，例如数组、链表或字符串。

并且满足以下任一目标：

• 检测循环或交点：需要判断一个链表或数组中是否有环，或者寻找两个链表的交点。
• 寻找中点或分位点：需要找到数据结构的特定分割位置。
  • 例如：寻找链表的中间节点（这常是归并排序等算法的第一步），或是寻找数组的某个四分位数位置。

掌握快慢指针，就像为你的算法工具箱添加了一件精巧的瑞士军刀。理解其原理后，你会发现它能优雅地解决一大类关于数据结构属性的问题。如果你有更多关于指针技巧或数据结构的心得，欢迎在云栈社区交流分享。