从淘汰赛到遍历深度：洛谷二叉树算法三题精讲与代码详解

二叉树作为兼具灵活性与实用性的核心数据结构，在算法设计与竞赛中地位举足轻重。其每个节点最多拥有两个子节点的特性，使其成为高效表示层级关系的理想模型。同时，它也为我们理解和应用递归思想提供了绝佳的实践场景。在信息学竞赛中，求解二叉树的深度与实现前序、中序、后序遍历是两类最基础且高频的问题，能否熟练解决它们，直接反映了我们对二叉树本质的理解程度。

下面，我们就结合洛谷（Luogu）平台上的三道经典题目，由浅入深地探讨二叉树的构建、遍历与深度计算。

T1. P4715 【深基16.例1】淘汰赛

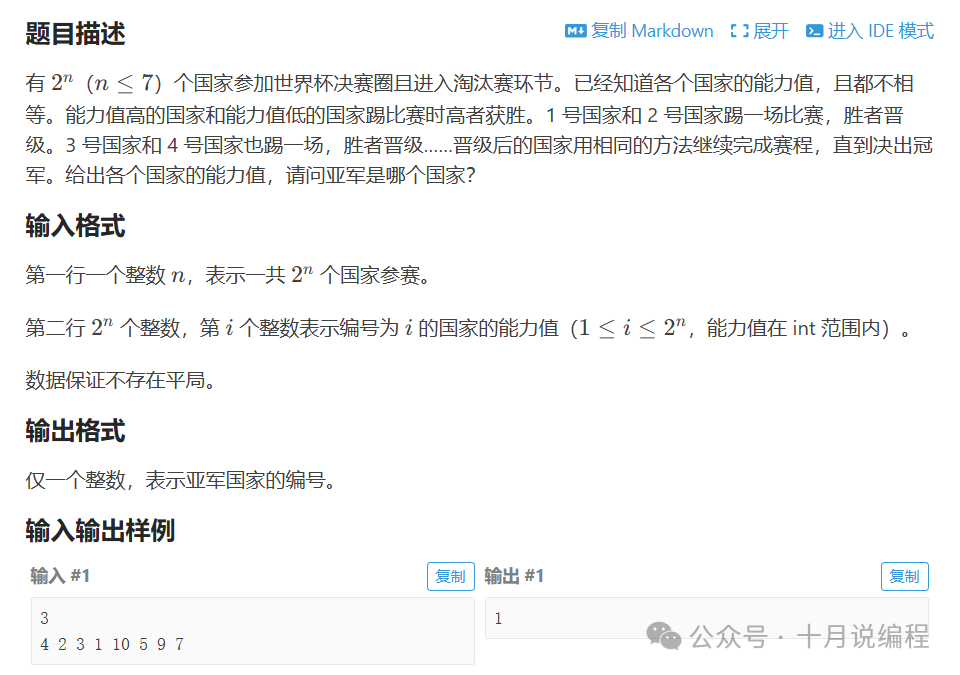
问题分析
题目模拟了世界杯淘汰赛的赛制：2^n 个国家两两对决，胜者晋级，直到决出冠军。我们需要根据各国的能力值，找出最终的亚军。

如何将这个问题与二叉树联系起来呢？比赛机制是相邻的两两PK，胜者进入下一轮。这里的每一对选手，就相当于一个父节点的左、右孩子，而胜出的选手则充当了这个父节点。整个赛程正好构成了一棵完全二叉树。

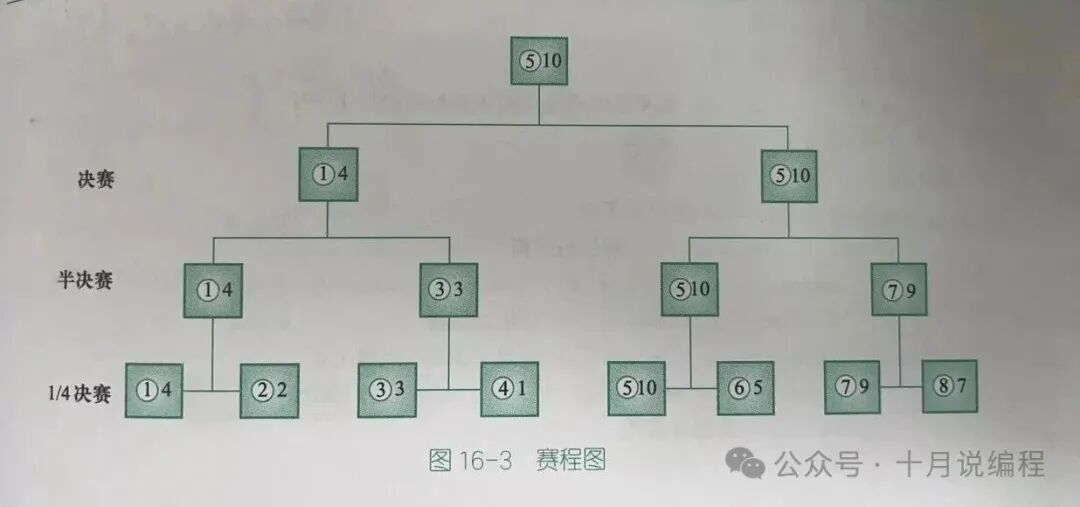
接下来是关键：如何存储比赛过程中的数据？我们观察这棵二叉树的编号规律。对于一棵用数组存储的完全二叉树，如果根节点编号为1，那么其左孩子编号为 2*x，右孩子编号为 2*x+1。第 k 层的节点个数是 2^(k-1)。为了放下所有 2^n 个初始国家，我们可以从编号 2^n 的位置开始存放它们的能力值和编号。

输入完成后，我们从根节点（编号1）开始进行深度优先搜索（DFS）。当搜索到叶子节点时（即编号 >= 2^n 的节点），开始向上回溯。在回溯过程中，比较左右子节点的能力值，将胜者的信息和能力值赋给父节点。这样，当回溯到根节点时，根节点记录的就是冠军的信息。亚军则是决赛中输给冠军的那个国家，即根节点左右子节点中能力值较大的那位。

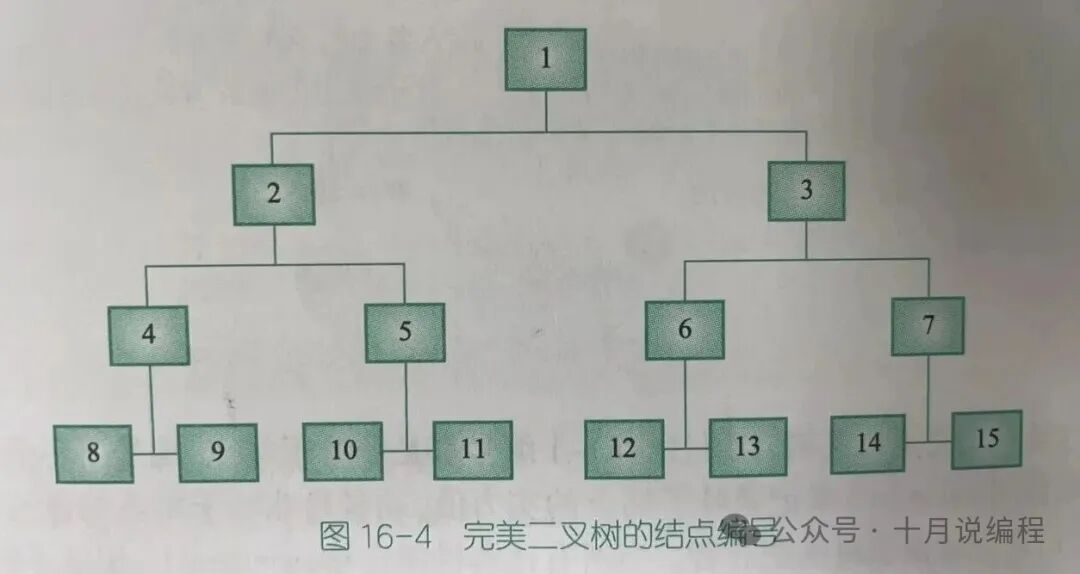
求解思路

1. 输入 n 和 2^n 个国家的能力值，将其存储在数组后半部分，并记录初始编号。
2. 从根节点（1号）开始进行DFS递归。
3. 当递归到叶子节点时返回，在回溯过程中比较左右孩子，更新父节点的信息为胜者。
4. 递归结束后，比较根节点的左右孩子（即进入决赛的两位选手），输出能力值较低者的编号，即为亚军。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N=1<<7;
struct node{
    int id;//编号
    int val;//权值
}a[2*N+1];
int n,start;
void dfs(int x){
    if(x>=start) return ;//到叶子节点 结束递归
    dfs(2*x);//递归左子树
    dfs(2*x+1);//递归右子树
    //回溯更新
    if(a[2*x].val>a[2*x+1].val) a[x].val=a[2*x].val,a[x].id=a[2*x].id;
    else a[x].val=a[2*x+1].val,a[x].id=a[2*x+1].id;
}
int main(){
    cin>>n;
    start=(1<<n);
    //输入2的n次方个数据
    for(int i=0;i<(1<<n);i++){
        cin>>a[start+i].val;//输入权值
        a[start+i].id=i+1;//记录编号
    }
    //递归分析
    dfs(1);//从根节点编号开始搜索
    //输出答案
    printf("%d",(a[2].val>a[3].val)?a[3].id:a[2].id);
    return 0;
}

T2. P1305 新二叉树

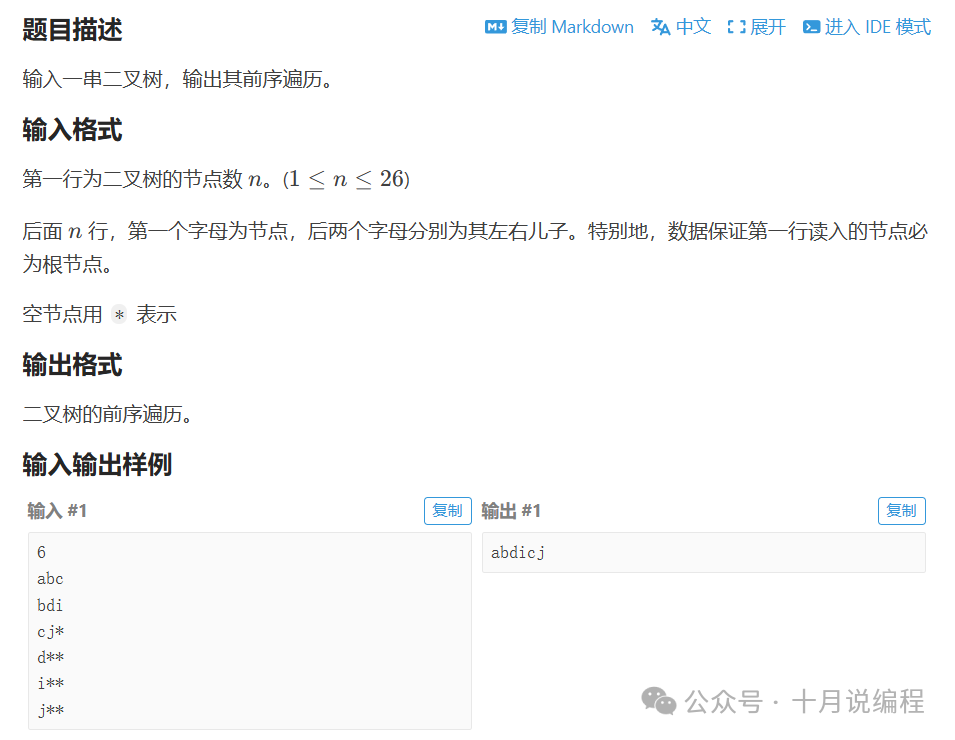
问题分析
题目直接给出了每个节点及其左右子节点的信息（用字母表示，*表示空），要求我们输出这棵二叉树的前序遍历序列。

当输入数据明确给出每个节点的左右孩子信息时，最适合使用“孩子表示法”来存储这棵树。这种方法为每个节点定义一个结构体，直接存储其左、右子节点的编号或指针。本题已经说明第一行读取的节点必为根节点，这为我们提供了便利。

求解思路

1. 定义一个字符转数字的函数，将 a~z 转为 1~26，将 * 转为 0。这样方便用数组索引。
2. 读入 n 行数据，每行包括父节点、左孩子、右孩子三个字符。
3. 利用孩子表示法，将转换后的编号存储到对应的结构体数组中。
4. 从根节点开始，进行深度优先搜索，按照“根 -> 左 -> 右”的顺序访问节点并输出。

备注：实现中序（左根右）或后序（左右根）遍历，只需调整访问根节点和递归左右子树的顺序即可。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+6;
struct node{
    int l,r;
}tree[30];
char fc,lc,rc;
int n,start,f,l,r;//转编号+1
void dfs_prev(int id){//前序遍历搜索函数
    if(!id) return ;//出口--叶子的子结点
    cout<<char(id-1+'a');//输出根节点
    dfs_prev(tree[id].l);//递归左子树
    dfs_prev(tree[id].r);//递归右子树
}
int ctoi(char c){//字符转数字
    if(c=='*') return 0;
    return c-'a'+1;
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>fc>>lc>>rc;//输入
        f=ctoi(fc),l=ctoi(lc),r=ctoi(rc);//转数字
        tree[f].l=l,tree[f].r=r;//存储左右孩子编号
        if(i==0) start=f;//记录起点编号
    }
    dfs_prev(start);//前序遍历 根左右
    return 0;
}

T3. P4913 【深基16.例3】二叉树深度

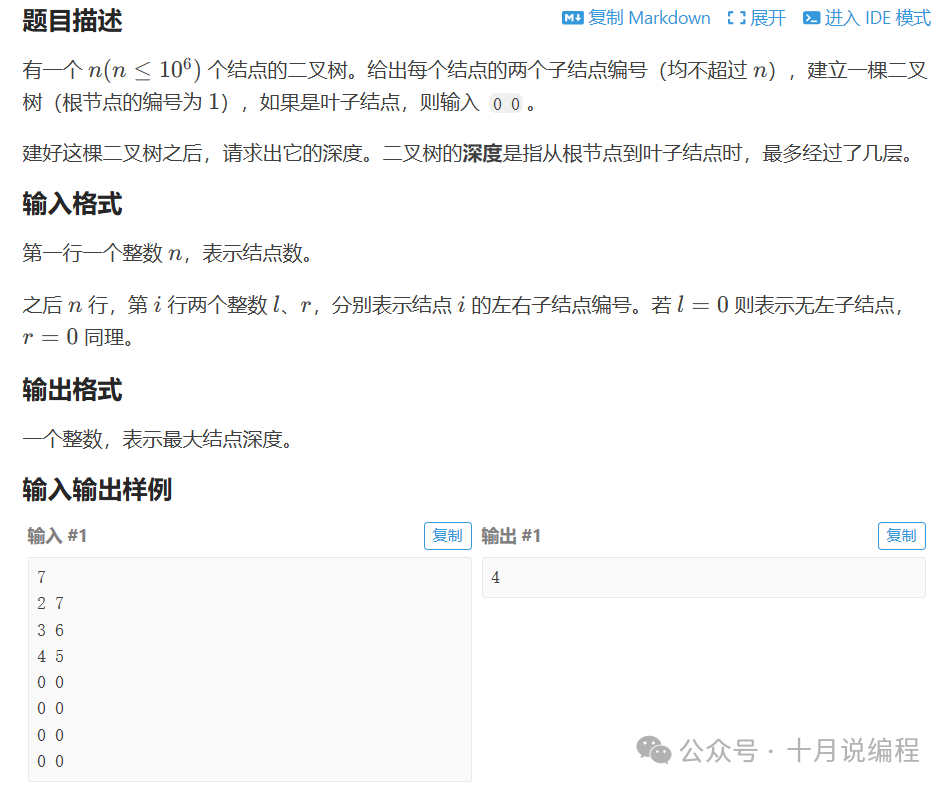
问题分析
题目给出了每个节点的左右子节点编号（0表示空），需要建立二叉树并计算其最大深度（从根节点到最远叶子节点经过的层数）。

这个问题同样适合使用孩子表示法。计算深度是一个典型的DFS过程：从根节点出发，每向下一层，当前深度加1。当到达空节点（叶子节点的子节点）时，说明一条路径已经走完，此时用当前深度更新全局最大深度。

求解思路

1. 根据输入，用孩子表示法存储二叉树结构。
2. 从根节点（编号1）开始DFS，参数包含当前节点编号和当前层数。
3. 如果当前节点为0，则到达了叶子节点的下一层，用当前层数更新答案并返回。
4. 否则，递归遍历左子树和右子树，层数加1。
5. DFS结束后，输出的最大层数即为二叉树深度。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+6;
struct node{
    int l,r;//左右孩子编号
}a[N];
int n,deep;
void dfs(int x,int step){
    if(!x){
        deep=max(deep,step);//更新答案
        return ;//到叶子节点的下一层
    }
    dfs(a[x].l,step+1);//递归左子树
    dfs(a[x].r,step+1);//递归右子树
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i].l>>a[i].r;//输入
    dfs(1,0);
    cout<<deep;
    return 0;
}

拓展练习

为了巩固对二叉树遍历的理解，可以尝试以下两道经典的遍历序列还原问题：

• T1. P1827 [USACO3.4] 美国血统 American Heritage：根据中序和后序遍历序列，求前序遍历序列。
• T2. P1030 [NOIP 2001 普及组] 求先序排列：根据中序和后序遍历序列，求前序遍历序列。

通过这三道题目的分析与实现，我们不仅掌握了二叉树孩子表示法的存储技巧，更深入理解了DFS递归在二叉树问题中的灵活应用。从模拟淘汰赛到实现遍历，再到计算深度，核心思想都是递归地对左右子树进行处理。希望这篇解析能帮助你更好地攻克二叉树相关题目。如果你有更好的解法或疑问，欢迎来云栈社区交流讨论。