
从量子力学课堂上耳熟能详的双缝实验出发,我们借一个广为流传的“费曼式追问”层层推进:从对两条路径振幅的相加,到多孔、多屏,再到把空间视为被无限细分的极限过程,最终引出“对所有路径求和”的费曼路径积分表述。通过这种由离散走向连续的直觉图景,路径积分不再只是形式主义中的抽象公式,而是量子叠加原理在时空中的自然延伸,并与时间演化算符、传播子以及统计物理中的配分函数建立起清晰联系。
一个“物理学课堂传说”
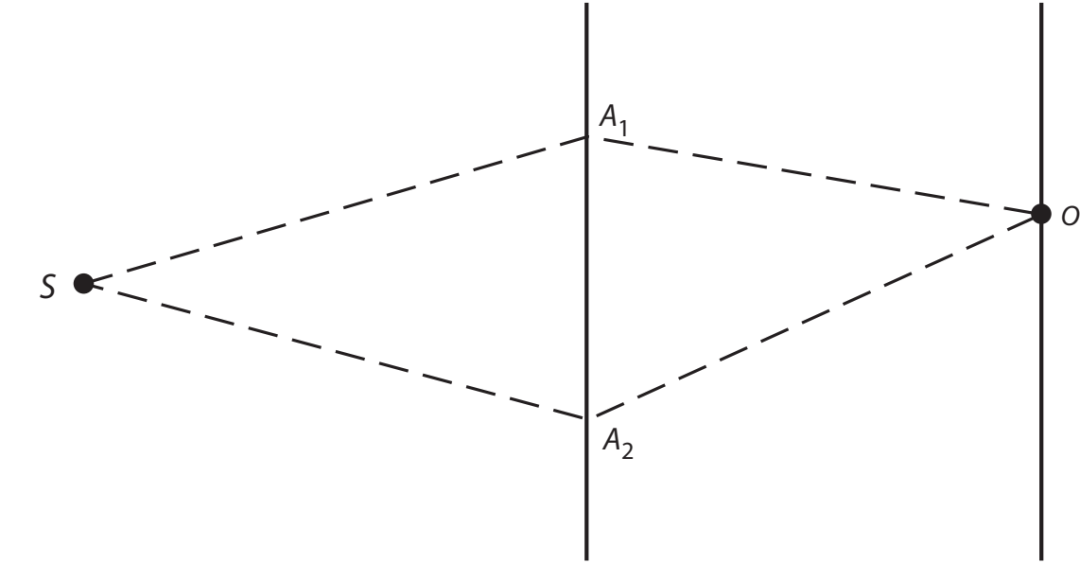
很久以前,一门量子力学课上,教授照例讲双缝实验:在时刻 t=0,粒子从源 S 发射,穿过屏幕上两个孔( A1 或 A2)之一,在时刻 t=T 被位于O的探测器探测到。
在标准讲法里,探测到的“概率”不是直接相加,而是先加“振幅”。根据量子力学的叠加原理,到达 O 的总振幅等于两条可能过程的振幅之和:
- 从 S经 A1 到的振幅
- 从 S 经 A2 到的振幅
这就是双缝干涉的数学核心:不同路径对应的振幅会相加,从而产生干涉。
这一点讲完后,故事的主角出现了——一个很聪明的学生(我们就叫他“费曼”)。
从“双缝”到“多缝”
费曼问:“教授,如果我在屏幕上再钻第三个孔呢?”
教授回答:“那就把三条过程的振幅相加。”
费曼又问:“如果我再钻第四个、第五个孔呢?”
教授终于有点不耐烦:“好吧,聪明人。全班都看得出来:我们就是把所有孔的振幅都加起来。”
为了把这句话说得更精确,我们记粒子从 S 出发,经由第 i 个孔 Ai,再到达 O 的振幅为 A(S → Ai → O)。
那么探测器在O处测到粒子的总振幅就是 A(detected at O) = Σi A(S → Ai → O)
这一步的意义很简单:孔从 2 个变成很多个,只是把“相加的项”从两项变成多项,本质仍是叠加原理。
但费曼还没停。
求和从“单屏”到“多屏”
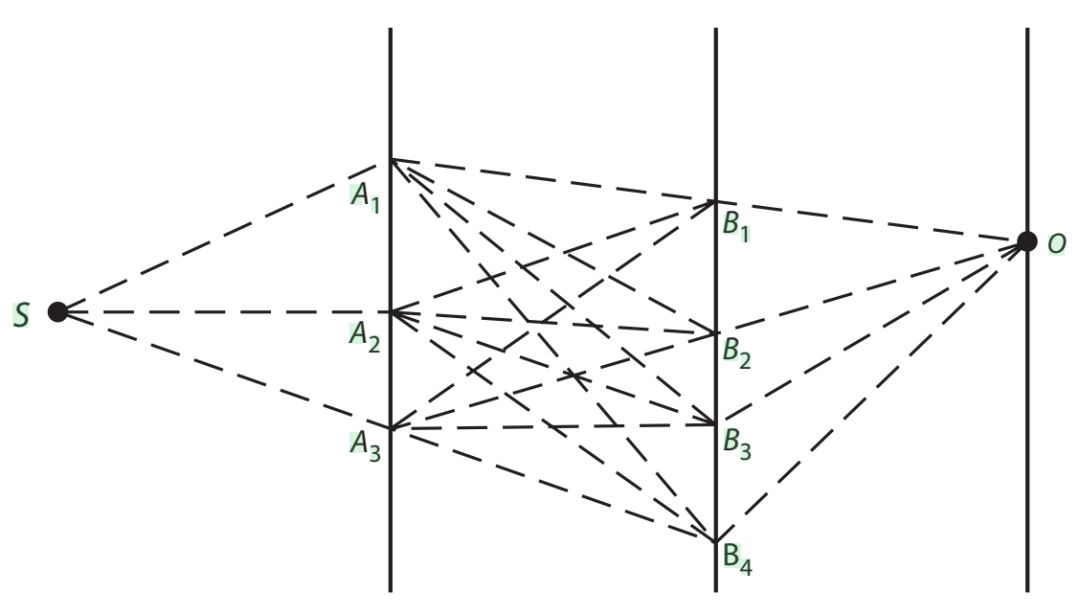
费曼继续追问:“如果我们再加一块屏,上面也钻一些孔呢?”
教授更烦了,说:“你看不出来吗?你只需要把过程拆成三段:
从源 S 到第一块屏的孔 Ai 再到第二块屏的孔 Bi ,再到探测器 O,然后对所有 i 和 j 求和就行了。”
也就是说,“一块屏多孔”对应的是对 i 求和;“两块屏多孔”对应对 i,j 做二重求和。叠加原理仍然没有变,只是中间可选节点更多了。
到这里,费曼的问题开始逼近关键点。
当所有屏幕“钻满孔”会变成什么?
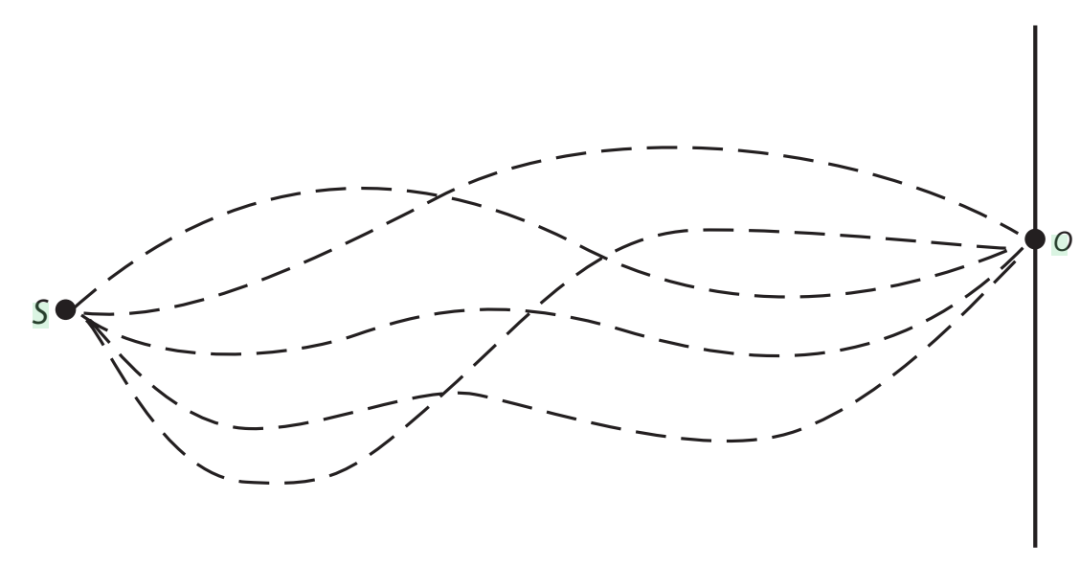
费曼继续纠缠:“那我再放第三块屏、第四块屏呢?如果我放一块屏,然后在上面钻无穷多个孔,使得这块屏等于不存在,那会怎样?”
教授不耐烦了:“我们往下讲吧,这门课要讲的内容还很多……”
这个故事里教授选择“跳过”,但聪明的读者朋友,你一定已经看出来费曼想干什么了。尤其妙的是那句话:在一块屏上钻出无穷多个孔,屏就等于不存在。
这句话把问题从“离散的孔”推向“连续的空间”:即使 S 到 O 之间什么都没有(只是空间),仍可以把传播理解为一种极限过程——好像空间被无穷多块屏“填满”,每块屏又被无穷多个孔“打穿”。于是粒子从 S 到 O 的振幅就变成:
不是挑一条路,而是把所有可能路径的贡献都加起来。
A(粒子在时间 T 内从 S 到 O) = Σ_paths A(粒子沿某条特定路径从 S 到 O)
这就是路径积分的直觉起点:从“对孔求和”升级为“对路径求和”。
“对所有路径求和”怎么定义?
到这一步,严谨的人会自然紧张:你说“对所有路径求和”,但“路径”是无限多、连续变化的对象,这个“求和”到底怎么定义?
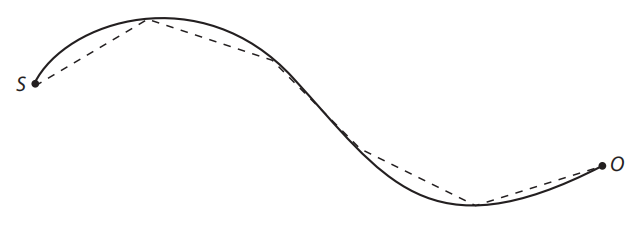
费曼(以及更早的狄拉克思路)采取的策略很经典:先离散化,再取极限。
做法是:
- 取一条连续路径,用很多段直线去逼近它。
- 让直线段越来越短、段数越来越多,使逼近趋于精确(段长趋于零)。
你会发现,这和“放很多块屏、屏间距无限小;每块屏上孔无限多”是一回事。它把“对路径的求和”变成了“对很多中间点的积分/求和”,最后再取极限。
一条路径的振幅怎么计算:用幺正性把小段乘起来
即使“路径的集合”被离散化了,还有一个关键问题:
沿某条特定路径传播的振幅 A(…) 怎么构造?
这里用到量子力学的一个结构:时间演化是幺正的。直观地说,如果你知道粒子在每个无穷小时间步(或无穷小空间段)上的传播振幅,那么一整段路径的振幅可以通过把这些“无穷小段的振幅”连续相乘得到。
也就是说:
- 把一条连续路径切成无穷多小段
- 每小段有一个传播振幅
- 整条路径的振幅就是这些小段振幅的乘积
最后再对“所有可能路径”求和(在极限意义下变成泛函积分),就得到路径积分形式主义的核心表达。
Dirac 的表述:从时间演化算符到“对路径求和”
前面的故事给出了路径积分的直觉:把所有可能路径的振幅加起来。费曼的路径积分不仅重构了量子力学,更成为了现代量子场论(QFT)的两大基石之一。
要让它成为可计算的理论,还需要一个更硬的起点。据说计算方法是Dirac先想出来的。他把“振幅”和“作用量”之间的关系提了出来,并且这关系可以从量子力学最标准的时间演化形式出发系统推导。
(1)传播振幅的起点:时间演化算符
在量子力学里,粒子从初始位置 qI 在时间 T 后到达末位置 qF 的传播振幅(传播子)写成
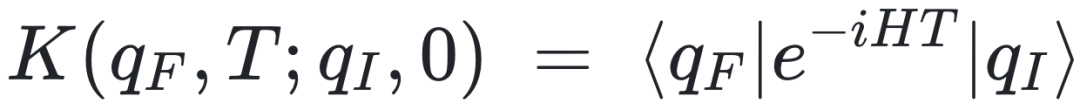
这里 H 是哈密顿量。这个式子几乎可以视作“量子力学演化”的定义。
这一点很重要:路径积分不是另外一套物理假设,它是同一个时间演化算符的另一种展开方式。
(2)时间切片:把 T切成很多个很小的步长
把总时间 T 切成 N 段,每段 ϵ=T/N
于是 e^{-iHT/ℏ} = (e^{-iHϵ/ℏ})^{N},接着在每两个短时间演化之间插入一次“完备性关系”(单位算符),用位置本征态写就是 1 = ∫ dq |q⟩⟨q|。
这样做的结果是:传播子被写成对所有中间位置的多重积分;每一小段只涉及一个“短时间传播核”:
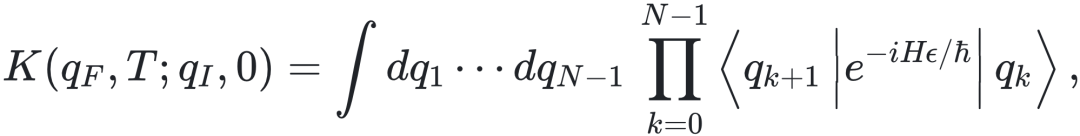
其中 q0=qI, qN=qF。这就是实现把一条路径积分起来、把所有路径加起来的过程:把一条连续路径变成许多小线段的极限;而“对所有路径求和”变成了“对所有中间点积分”。
(3)计算无穷小的时间核
接下来关键是计算短时间振幅 的形式。做法是:在坐标表象里插入动量完备性 ,并利用短时间近似(ϵ很小)把指数展开到合适阶。对于一般的哈密顿量 ,振幅会变成这个样子。在计算的过程中,哈密顿量会自然变形为拉格朗日量,最终指数里出现的是作用量 。
(4)与统计物理的关联
在大多数情况下,我们关心的是把初态 |I〉与末态 |F〉都取成基态 |0〉。按惯例,我们把真空到真空的演化振幅记为 Z:Z ≡ ⟨0|e^{-iHT}|0⟩。
实时间路径积分之所以“可用”,主要依赖不同路径带来的快速振荡相位在求和时相互抵消,从而在物理意义上起到“收敛”的作用;更为严格的处理是进行所谓的 Wick 旋转,把时间变换到 Euclidean(虚)时间 Τ。这相当于作代换 t=-iΤ(并在复 t 平面上旋转积分路径),使权重从振荡的 exp(iS/ћ) 变为指数衰减的 exp(-SE/ћ),从而得到 Euclidean 路径积分,这种形式与统计物理的玻尔兹曼权重 exp(-βE) 在结构上完全一致:Euclidean 作用量 SE 扮演“能量泛函”的角色,因此路径积分变成对所有配置的加权求和。
更进一步,在有限温度量子统计中,配分函数 Z(β)=Tr e^{-βH} 也可写成 Euclidean 路径积分,其关键在于“取迹”对应 Euclidean 时间方向的周期化:对玻色自由度满足 q(β)=q(0) (费米自由度满足反周期边界条 ψ(β)=-ψ(0)),于是 β 直接等同于 Euclidean 时间圆周的长度。这样一来,量子场论在虚时间下的计算形式,会变得非常像统计物理里计算配分函数的方式。
到这里,我们其实完成了一次很朴素的“极限过渡”:从双缝的两条可能过程出发,逐步把“对离散选项求和”推到“对连续路径求和”。技术上,它并没有另起炉灶,仍从最标准的时间演化算符出发;直觉上,它只是把空间想象成被越来越密的“中间位置”填满,再把这些中间位置的贡献在极限意义下叠加起来。这样,路径积分既保留了量子叠加的核心,也提供了一种把量子动力学写成“权重求和”的表达方式。
同时也应当看到,“对所有路径求和”这句话之所以能落地,依赖一套明确的规则:离散化、短时传播子的近似计算,以及在需要时通过 Wick 旋转把振荡权重变成更稳定的 Euclidean 权重。正因为这些步骤把形式主义变成了可操作的计算框架,路径积分才能自然连接到传播子、真空振幅 Z,并进一步与统计物理的配分函数结构对应起来。接下来若要继续深入,关键问题就会从“它是什么”转向“怎么用”:在具体体系里如何选取合适的近似、如何处理相互作用项,以及在场论中如何理解测度、算符排序与重整化等更细的技术环节。
关于物理学中更深入的 逻辑 和 数学 推演,可以参阅 云栈社区 上的相关讨论。此外,本文的推导过程也展示了从基础概念出发,运用 离散数学 的极限思想,最终构造出强大物理工具的全过程,这本身也是 计算机基础 思维在理论物理中的一次精彩应用。
参考文献:
Zee, A. (2010). Quantum field theory in a nutshell (2nd ed.). Princeton University Press.