对称二叉树LeetCode题解：递归算法判断二叉树对称性详解

题目介绍

给定一个二叉树的根节点 root，要求检查这棵树是否是轴对称的。

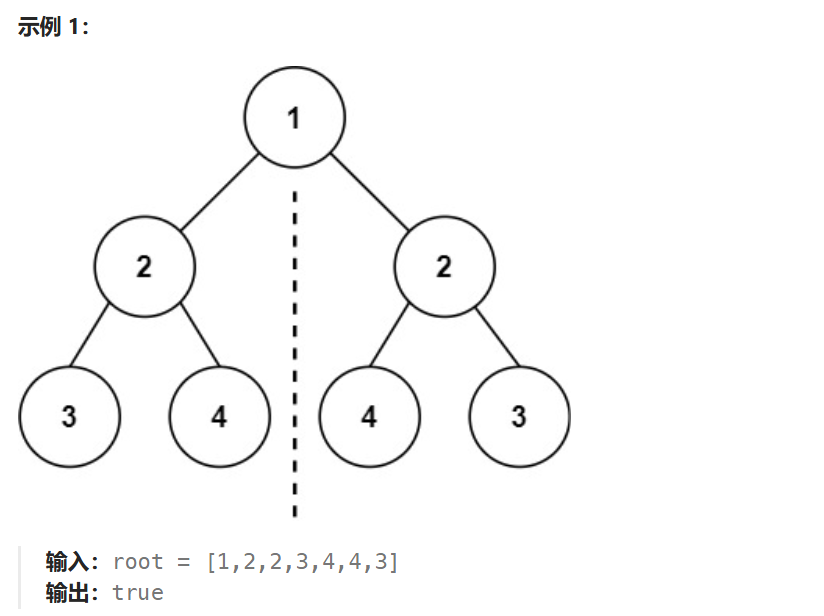
输入：root = [1,2,2,3,4,4,3]
输出：true

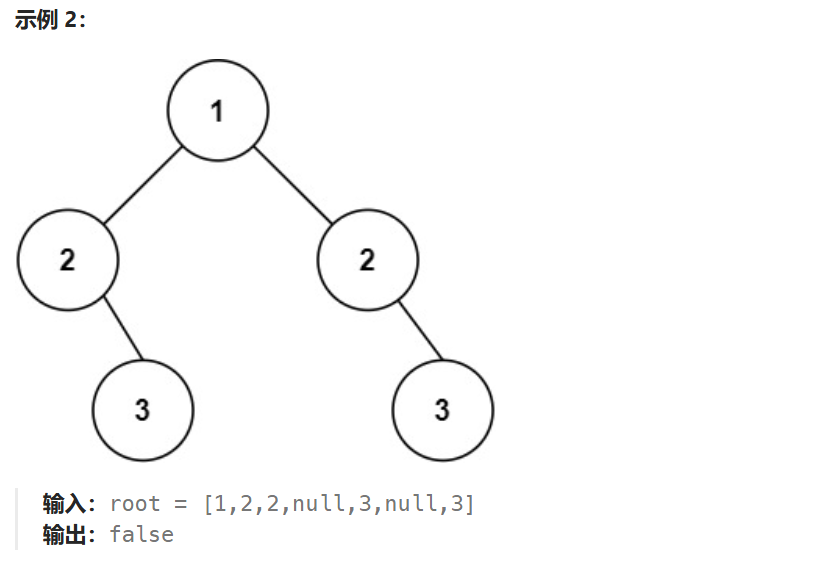
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

题目给出的初始代码框架如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {

    }
};

解题思路解析

本题的目标很明确：给定一棵二叉树（以根节点代表整棵树），判断其结构是否对称。

核心思路：递归

解决此类树结构对称性问题，递归是一种非常直观且有效的方法。递归的核心在于定义清楚递归任务和递归终止条件。

问题转化：判断一棵树是否对称，等价于判断其左右子树是否镜像对称。而要判断两棵树（A和B）是否镜像对称，需要满足：

1. 两棵树的根节点值相等。
2. A树的左子树与B树的右子树镜像对称。
3. A树的右子树与B树的左子树镜像对称。

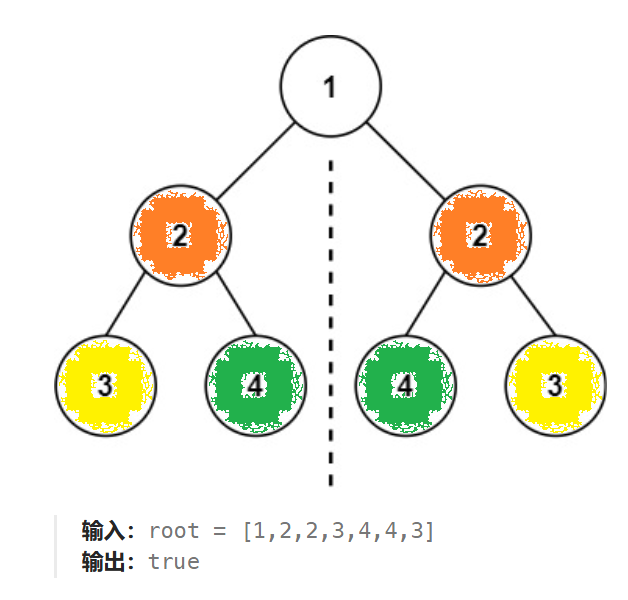
上图清晰地展示了判断对称性需要“交叉”比较左右子树的逻辑，这正是递归思路的雏形。

递归函数设计

基于上述分析，我们设计一个辅助函数来承担核心的递归判断任务。这个函数需要接收两个树节点，代表待比较的两棵（子）树。

我们将其定义为：bool _isSymmetric(TreeNode* p, TreeNode* q)

递归终止条件（Base Case）：

1. 如果 p 和 q 都为空，那么这两棵空树是对称的，返回 true。
2. 如果 p 和 q 只有一个为空，或者两者的值不相等，那么不对称，返回 false。

递归任务：
在排除了终止条件后（即 p 和 q 均不为空且值相等），递归地判断：

• p 的左子树与 q 的右子树是否对称。
• p 的右子树与 q 的左子树是否对称。

只有当这两个条件都满足时，当前两棵树才对称。

递归过程图解

下图概括了递归函数的判断逻辑：

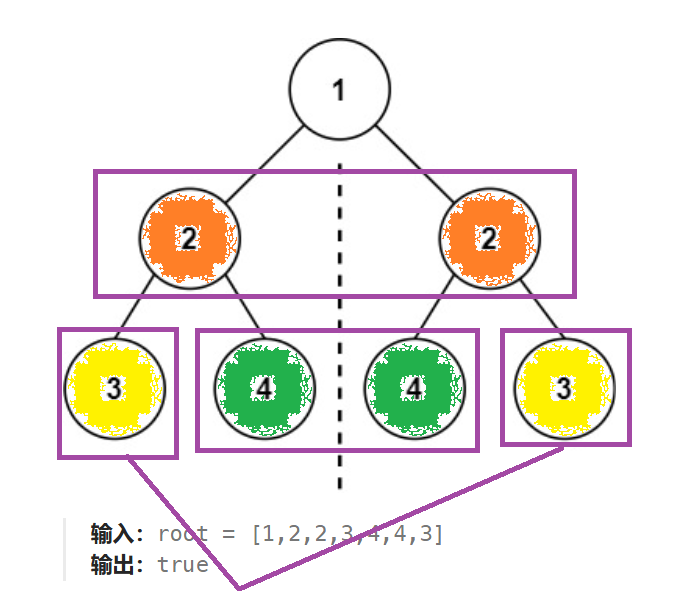
代码实现

理解了递归思路后，代码的实现便水到渠成。

首先实现核心的递归辅助函数：

bool _isSymmetric(TreeNode* p, TreeNode* q) {
    // 递归出口：两者都为空
    if (p == nullptr && q == nullptr) return true;
    // 递归出口：一个为空或值不等
    if (p == nullptr || q == nullptr || p->val != q->val) return false;
    // 递归任务：交叉判断子树
    return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);
}

然后，在题目要求的入口函数中调用它，初始传入整棵树的左右子树：

bool isSymmetric(TreeNode* root) {
    // 防御性编程，虽然题目说节点数>=1
    if (root == nullptr) return true;
    // 判断整棵树的左右子树是否对称
    return _isSymmetric(root->left, root->right);
}

完整参考代码

将上述两部分组合，得到完整的C++解决方案。这道题是深入理解递归在数据结构中的应用的经典案例，其“分而治之”的思想在解决许多二叉树问题上都非常有效。

class Solution {
public:
    // 递归辅助函数，判断两棵树是否镜像对称
    bool _isSymmetric(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr) return true;
        if (p == nullptr || q == nullptr || p->val != q->val) return false;
        return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);
    }

    // 主函数
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return _isSymmetric(root->left, root->right);
    }
};

总结

解决“对称二叉树”问题的关键在于将“判断单棵树是否对称”转化为“判断两棵树是否镜像对称”，并递归地应用这一规则。

解题步骤：

1. 定义递归函数，明确功能是判断两棵子树 (p, q) 是否对称。
2. 确定递归出口：两子树均为空（对称），或一空一非空/值不相等（不对称）。
3. 确定递归任务：判断 p->left 与 q->right 对称，且 p->right 与 q->left 对称。
4. 在主函数中，调用递归函数判断整棵树的左右子树。

这种递归分解问题的思想是算法学习中的核心，不仅适用于二叉树，也广泛用于其他数据结构的处理。掌握其本质后，即使换用其他语言如Go来实现，思路也完全一致。