动量法原理与实战：从梯度下降优化到股票预测的算法解析

“动量法”（Momentum）是一个在多领域——从物理学、金融投资到机器学习优化——都极具影响力的概念。本文将从其核心思想出发，结合公式推导与一个完整的Python代码案例，深入解析动量法的工作原理及其在趋势预测中的应用。

理解动量法的核心思想

动量法的命名直接源于物理学中的“动量”概念。在物理世界中，一个质量大、速度快的物体拥有更大的动量，使其更倾向于保持原有的运动状态。将这一思想抽象出来：如果一个事物在一段时间内持续朝某个方向运动（发展），那么它很可能在接下来的一段时间内继续保持这一趋势。

动量法正是利用历史的表现（“趋势”或“速度”）来预测未来的发展方向。

跨领域的直观示例

1. 物理世界：用力推一个滑板上的小球，它会加速并保持一段时间的滚动。若没有大的阻力，其滚动趋势（动量）将持续。
2. 金融投资：一只股票若连续多日上涨，投资者常认为其积累了“上涨动量”，未来继续上涨的可能性较大。反之，连续下跌的股票则可能被认为存在“下跌动量”。
3. 机器学习：在优化算法如梯度下降中引入动量项，可以有效帮助模型参数更新冲出局部最小值或平稳区域，加速收敛过程。

动量法的数学表示与公式推导

在数学上，动量法通常表述为根据历史变化来平滑地更新当前值。一个常见的更新公式如下：

假设我们追踪一个变量（如价格）的动量（速度）v_t，其更新规则为：
v_t = β * v_{t-1} + (1 - β) * Δx_t

其中：

• v_t：当前时刻t的动量值。
• β：动量衰减系数（0 < β < 1）。β值越大，历史动量的权重越高，更新越平滑。
• Δx_t：当前时刻的瞬时变化量（如t时刻与t-1时刻的价格差）。

基于更新后的动量，我们可以对下一个状态进行预测：
predicted_t = predicted_{t-1} + v_t

这个公式体现了“当前更新方向不仅受瞬时变化影响，也继承了过去的变化趋势”的核心思想。

实战案例：基于动量法的股票价格预测

以下我们使用Python，通过模拟的股票价格时间序列数据，演示如何应用动量法进行趋势预测。

import numpy as np
import matplotlib.pyplot as plt

# 1. 生成模拟股票价格数据
np.random.seed(42)
n = 1000  # 数据点数量
time = np.arange(n)
initial_price = 100
# 生成正态分布的价格波动序列
price_changes = np.random.normal(loc=0, scale=1, size=n)
# 累积波动，生成价格序列
price_data = initial_price + np.cumsum(price_changes)

# 2. 动量法参数初始化
beta = 0.9  # 动量衰减系数
v = np.zeros(n)  # 动量数组
predicted_price = np.zeros(n)  # 预测价格数组
predicted_price[0] = price_data[0]  # 初始化第一个预测值

# 3. 应用动量法进行迭代预测
for t in range(1, n):
    delta_x = price_data[t] - price_data[t-1]  # 计算瞬时变化
    v[t] = beta * v[t-1] + (1 - beta) * delta_x  # 更新动量
    predicted_price[t] = predicted_price[t-1] + v[t]  # 生成预测

# 4. 可视化结果
fig, axs = plt.subplots(2, 2, figsize=(14, 10))

# 图1: 实际价格 vs 预测价格
axs[0, 0].plot(time, price_data, label="Actual Price", color='blue', alpha=0.7)
axs[0, 0].plot(time, predicted_price, label="Predicted Price", color='red', linestyle='--')
axs[0, 0].set_title('Actual vs Predicted Price')
axs[0, 0].set_xlabel('Time')
axs[0, 0].set_ylabel('Price')
axs[0, 0].legend()

# 图2: 价格变动 (Delta)
price_changes_display = np.diff(price_data)
axs[0, 1].plot(time[1:], price_changes_display, color='green', alpha=0.8)
axs[0, 1].set_title('Price Change (Delta)')
axs[0, 1].set_xlabel('Time')
axs[0, 1].set_ylabel('Price Change')

# 图3: 动量变化
axs[1, 0].plot(time[1:], v[1:], label="Momentum", color='orange')
axs[1, 0].set_title('Momentum Change Over Time')
axs[1, 0].set_xlabel('Time')
axs[1, 0].set_ylabel('Momentum')
axs[1, 0].legend()

# 图4: 价格变动 vs 动量变化
axs[1, 1].plot(time[1:], price_changes_display, label="Price Change", color='green', alpha=0.7)
axs[1, 1].plot(time[1:], v[1:], label="Momentum", color='orange', linestyle='--')
axs[1, 1].set_title('Price Change vs Momentum')
axs[1, 1].set_xlabel('Time')
axs[1, 1].set_ylabel('Change')
axs[1, 1].legend()

plt.tight_layout()
plt.show()

结果解读与代码分析：

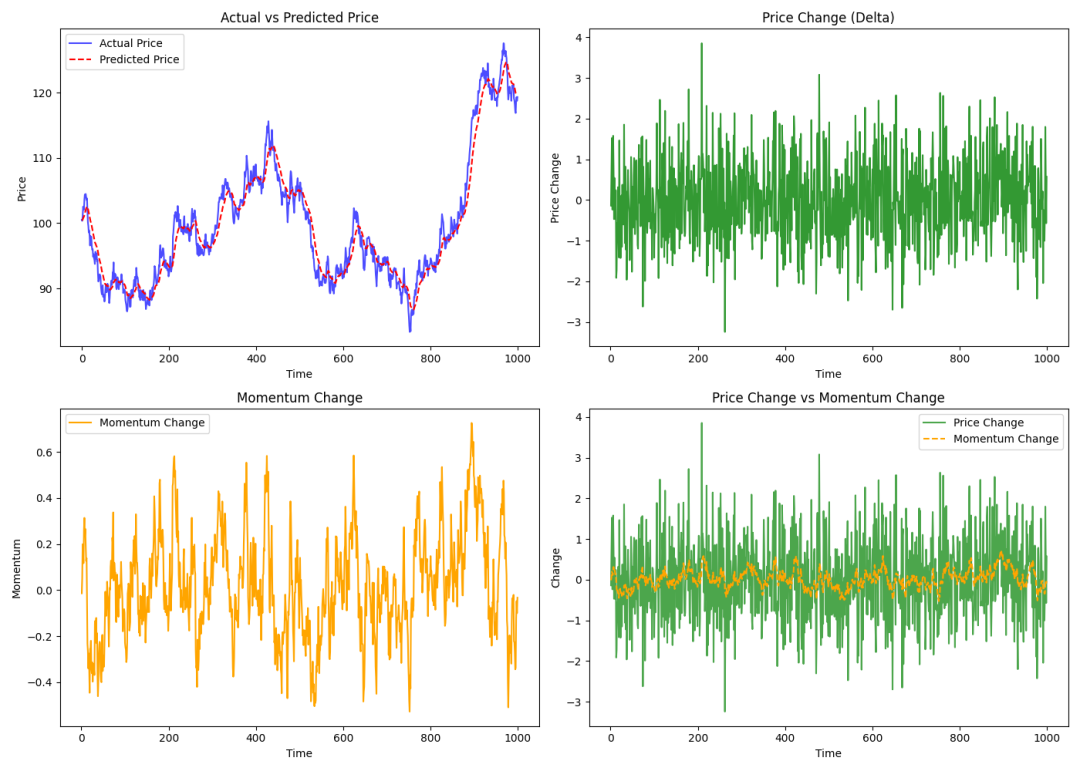
1. 图1：实际vs预测价格：红色虚线（预测价格）紧密跟随蓝色实线（实际价格）的长期趋势，但在剧烈波动处存在滞后。这体现了动量法“平滑趋势，过滤噪声”的特性。
2. 图2：价格瞬时变动：展示了每个时间点原始的价格变化Δx_t，波动剧烈。
3. 图3：动量变化：展示了计算出的动量值v_t。相比原始变动，动量曲线更加平滑，它是对历史变动趋势的加权平均。
4. 图4：变动对比：直观对比原始价格变动与平滑后的动量。可以看到动量有效地减弱了短期噪声，突出了主要趋势方向。

本例通过Python与NumPy实现，清晰地展示了动量法如何从历史数据中提取“趋势”信息，并用于未来值的预测。这种方法在趋势明显的场景下简单而有效，不仅是金融预测的基础工具，其思想更是深度优化算法（如带动量的随机梯度下降）的核心组成部分。