递归与分治算法核心剖析：原理、差异与LeetCode实战应用

递归（Recursion）与分治（Divide and Conquer）是算法与数据结构领域的核心思想，尤其对解决树、图、排序等问题至关重要。它们思想相似但各有侧重，理解其内在联系与差异是掌握高级算法的基础。

递归算法详解

递归是一种通过函数调用自身来解决问题的编程范式。它将一个复杂的大问题，分解为若干个相同类型但规模更小的子问题，直到子问题简单到可以直接求解（即基准情况）。递归以其代码简洁优雅的特性，特别适合处理具有自相似结构的问题。

其核心在于两点：必须存在能使递归终止的基准情况（Base Case）；且每次递归调用都必须向基准情况靠近，避免无限循环。

算法核心步骤

1. 定义递归函数：明确函数功能、输入参数和返回值。
2. 确定基准情况：识别最简单、无需递归即可直接求解的情况。
3. 分解与递归调用：将原问题分解为更小的子问题，并递归调用自身解决。
4. 组合结果：利用子问题的解，组合出原问题的解。

递归的空间复杂度通常与递归深度成正比，因为需要维护函数调用栈；时间复杂度则取决于递归深度和每层递归的工作量。

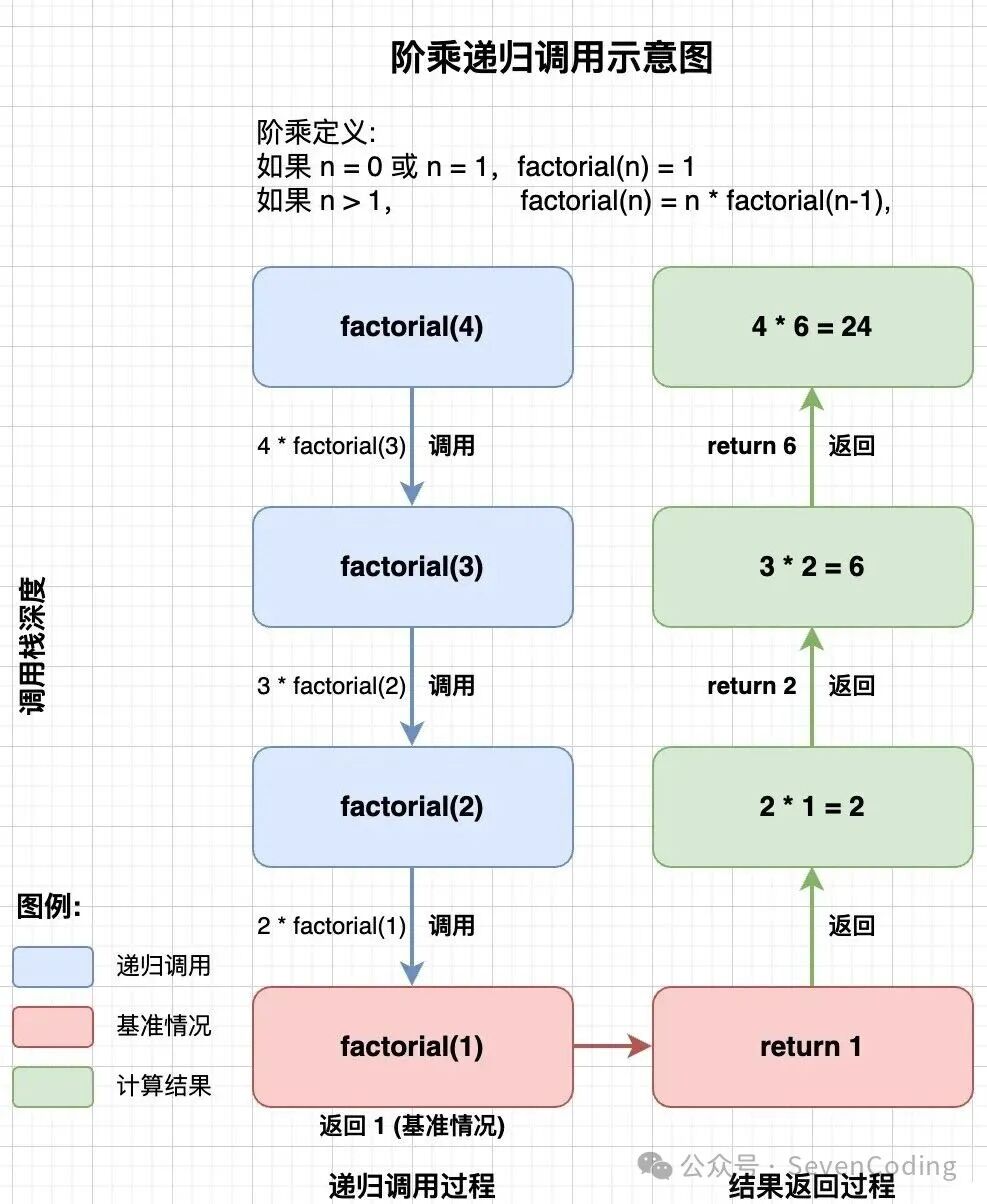
基础实现：阶乘计算

以计算阶乘（factorial）为例，直观展示递归如何将问题 n! 转化为子问题 (n-1)!。

public class Factorial {
    public static int factorial(int n) {
        // 基准情况：0! 和 1! 都等于 1
        if (n == 0 || n == 1) {
            return 1;
        }

        // 递归分解：n! = n * (n-1)!
        return n * factorial(n - 1);
    }

    // 测试
    public static void main(String[] args) {
        for (int i = 0; i <= 10; i++) {
            System.out.printf("%d! = %d\n", i, factorial(i));
        }
    }
}

递归的优化策略

递归虽优雅，但可能存在栈溢出和重复计算的风险。常见的优化手段包括：

1. 尾递归优化

将递归调用置于函数的最后一步（尾位置），某些编译器或运行时（如JVM在某些条件下）可对其进行优化，避免额外的栈帧开销，但其效果依赖于语言本身的支持。

public static int factorialTailRecursive(int n) {
    return factorialHelper(n, 1);
}

private static int factorialHelper(int n, int accumulator) {
    // 基准情况
    if (n == 0 || n == 1) {
        return accumulator;
    }
    // 尾递归调用
    return factorialHelper(n - 1, n * accumulator);
}

2. 记忆化递归

通过缓存（通常用数组或哈希表）存储已计算过的子问题结果，当再次遇到相同子问题时直接返回缓存值，避免重复计算。这是优化诸如斐波那契数列等问题的有效方法，也是动态规划思想的雏形。

public static int factorialMemoization(int n) {
    int[] memo = new int[n + 1];
    return factorialWithMemo(n, memo);
}

private static int factorialWithMemo(int n, int[] memo) {
    if (n == 0 || n == 1) {
        return 1;
    }
    // 检查缓存
    if (memo[n] != 0) {
        return memo[n];
    }
    // 计算并存入缓存
    memo[n] = n * factorialWithMemo(n - 1, memo);
    return memo[n];
}

优缺点与应用场景

优点：

• 代码简洁，逻辑清晰，能直接反映问题的数学定义或自然结构。
• 非常适合处理递归定义的数据结构，如树、图的遍历。

缺点：

• 函数调用开销大，递归过深易导致栈溢出。
• 可能存在大量重复计算，效率低下。

典型应用场景：

• 数学计算：阶乘、斐波那契数列。
• 数据结构操作：二叉树遍历（前序、中序、后序）、图的深度优先搜索（DFS）。
• 分治与排序：归并排序、快速排序。
• 回溯算法：八皇后、数独求解。

LeetCode 递归实战题目

• 21. 合并两个有序链表：递归合并链表的经典案例。
• 104. 二叉树的最大深度：理解递归在树结构中的应用。
• 509. 斐波那契数：对比朴素递归与记忆化递归的效率差异。

分治算法详解

分治法采用“分而治之”的策略，其核心是将一个难以直接解决的大问题分解成若干个规模较小的子问题，这些子问题相互独立且与原问题形式相同。然后递归地解决各子问题，最后将子问题的解合并，得到原问题的解。

与单纯递归相比，分治更强调“分”、“治”、“合”这三个清晰的阶段，且子问题之间通常没有重叠。

算法核心步骤

1. 分解：将原问题分解为多个子问题。
2. 解决：递归求解各子问题。若子问题足够小，则直接求解。
3. 合并：将子问题的解合并成原问题的解。

分治法的效率很大程度上取决于合并步骤的复杂度。其天然适合并行计算，因为独立的子问题可以同时求解。

优缺点与应用场景

优点：

• 能有效降低问题复杂度，常能带来多项式级别的效率提升。
• 子问题独立，易于并行化。

缺点：

• 递归带来的开销。
• 若子问题不独立（存在重叠），则效率可能低于动态规划。
• 合并过程有时较为复杂。

典型应用场景：

• 排序算法：归并排序（典型分治）、快速排序。
• 搜索算法：二分查找。
• 高效计算：Strassen矩阵乘法、快速傅里叶变换（FFT）、Karatsuba大整数乘法。
• 经典问题：棋盘覆盖、最近点对问题。

LeetCode 分治实战题目

• 53. 最大子数组和：练习如何分解和合并子问题解。
• 215. 数组中的第K个最大元素：利用快速排序的分区思想（分治变种）。
• 23. 合并K个升序链表：通过分治法两两合并，降低时间复杂度。
• 169. 多数元素：尝试用分治思路解决投票问题。
• 240. 搜索二维矩阵 II：利用矩阵特性进行分治搜索。

总结：递归与分治的关系

递归是实现分治（以及动态规划、回溯）的常用编程技巧，它描述了函数自我调用的过程。而分治是一种更上层的算法设计思想，它明确了“分-治-合”的解决问题框架。可以说，分治算法通常用递归来实现，但并非所有递归算法都符合分治模式（例如，普通的树遍历是递归，但不一定涉及“合并”步骤）。理解这一点，有助于在解决实际问题时灵活选用和组合不同的算法思想。