C语言递归编程详解：核心原理、应用场景与实战案例

1. 基础概念

1.1 函数递归的定义

在编程中，一种程序调用自身的技巧被称为递归（Recursion）。

递归作为一种算法思想，在程序设计语言中应用广泛。它指的是一个过程或函数在其定义或说明中，直接或间接地调用自身的一种方法。

其核心思想在于，通常将一个大型复杂的问题，层层转化为一个与原问题相似但规模更小的问题来求解。

1.2 函数递归的优缺点

• 优点：使用递归，通常只需少量代码就能描述出解题过程中所需的多次重复计算，极大地减少了代码量。递归的主要思维方式是“大事化小”，这种自上而下分解问题的思路对于解决复杂问题非常重要。
• 缺点：
  1. 栈溢出风险：如果递归使用不当，例如缺少终止条件或深度过大，会导致栈溢出。因为每一次函数调用都会在内存的栈区申请空间。
  2. 性能开销：每一次函数调用（包括递归调用）都会在栈上创建新的函数栈帧（压栈），涉及参数传递、局部变量分配等操作。这可能会降低代码的执行效率，尤其是在递归深度很大时（后续在斐波那契数列的例子中会具体解释）。

1.3 函数递归的必要条件

一个有效的递归函数必须满足两个条件，否则将导致无限递归或逻辑错误：

1. 存在限制条件（递归出口）：当满足此条件时，递归不再继续，开始逐层返回。
2. 每次递归调用后都更接近限制条件：确保递归过程能够朝着终止条件的方向推进，避免无限循环。

2. 入门级函数递归例题

2.1 函数递归之死循环

了解了递归的基本概念后，我们先来看一段有趣但危险的代码，它揭示了递归使用不当的后果。

#include<stdio.h>
int main()
{
    printf("cc\n");
    main();   //重复调用main函数
    return 0;
}

可以预见，这个程序最终会崩溃。因为它无限地调用 main 函数，每一次调用都在栈上开辟新的空间，却没有任何返回。这种“死递归”会迅速消耗尽栈空间，导致栈溢出(Stack Overflow)，这也对应了前面提到的缺点。

2.2 顺序打印整数的每一位

题目描述：
接受一个无符号整型值，按顺序打印它的每一位。例如：输入 1234，输出 1 2 3 4。

解题思路：处理数字的各位，通常要想到除法和取模运算。同时，必须设计好限制条件，并确保每次递归后都更接近这个条件。
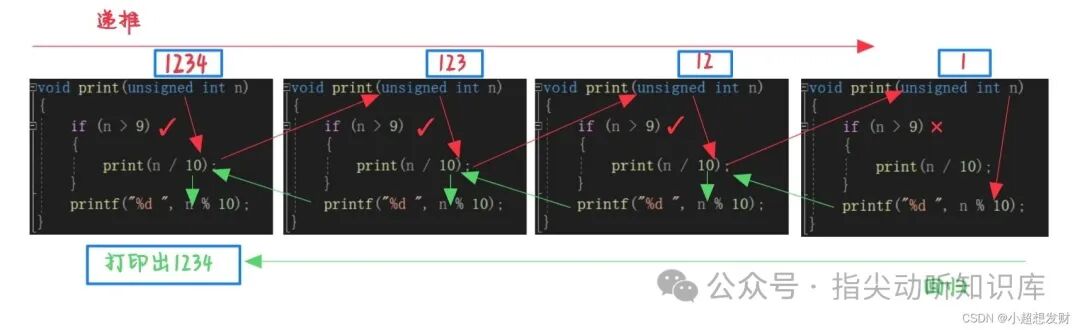
思路是递归递推：1234%10=4， 123%10=3， 12%10=2， 1%10=1。我们设定限制条件 n>9，当 n 被除到小于等于9时，直接打印其个位，然后递归回归，倒序打印出之前每一位的结果，最终组合成 1 2 3 4。

设n为1234
print(1234/10) + 1234%10 (=4)
print(123/10) + 123%10（=3）
print(12/10) + 12%10（=2）

当 n 最终为 1 时，不满足限制条件 n>9，直接打印 1%10（结果为 1），然后开始返回。

代码实现：

void print(unsigned int n)
{
    if (n > 9)     //限定条件
    {
        print(n / 10);  //递归调用，去掉最后一位
    }
    printf("%d ", n % 10);  //取余，打印当前最后一位
}

int main()
{
    unsigned int n = 0;
    scanf("%u", &n);
    //按顺序打印1234
    print(n);
    return 0;
}

3. 典型例题的实现

3.1 求n的阶乘

题目描述：
用递归方法求 n 的阶乘（暂不考虑溢出）。例如：输入 4，输出 24。

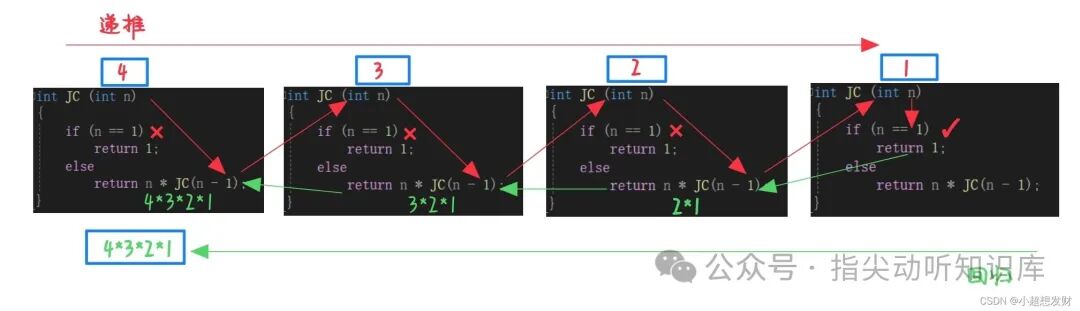
解题思路：n 的阶乘是 1*2*3*...*n。采用递归的“大事化小”思想：n! = n * (n-1)!。我们可以先递推计算 (n-1)!，再用其结果乘以 n。以 n==1 作为限制条件，此时 1! = 1，然后开始回归，依次计算并返回各层的阶乘值。

JC(n)
n * JC(n-1)
n * (n-1) * JC(n-2)
n * (n-1) * (n-2) * JC(n-3)
...
n * (n-1) * (n-2) * ... * JC(1)

当满足限制条件 n==1 时，返回 1，然后逐层回归计算。

代码实现：

int JC(int n)
{
    if (n == 1)
        return 1;
    else
        return n * JC(n - 1);        //阶乘的递归实现方式
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    int ret = JC(n);
    printf("n的阶乘为：%d", ret);
    return 0;
}

3.2 strlen函数的模拟实现

题目描述：
用递归方法模拟实现 strlen 函数。例如：输入字符串 "abc"，输出 3。

解题思路：标准 strlen 函数遇到字符串结束符 \0 停止计数。我们以此作为限制条件。每次递归调用时，如果当前字符不是 \0，则字符串长度加1，并对下一个字符位置（str+1）继续调用函数。这本质上是将遍历字符串的循环改写为了递归形式，属于算法中遍历思想的一种体现。

my_strlen("abc\0")
1 + my_strlen("bc\0")
1 + (1 + my_strlen("c\0"))
1 + (1 + (1 + my_strlen("\0")))

当遇到 \0 时，满足限制条件，返回 0，然后开始回归累加。

代码实现：

int my_strlen(char* str)
{
    if (*str != '\0')
        return 1 + my_strlen(str + 1);    //strlen函数的模拟实现方式
    return 0;
}

int main()
{
    char arr[] = "abc";
    int ret = my_strlen(arr);
    printf("%d", ret);
    return 0;
}

3.3 求n的k次幂

题目描述：
用递归方法实现 n 的 k 次幂。例如：输入 3, 3，输出 27.0。

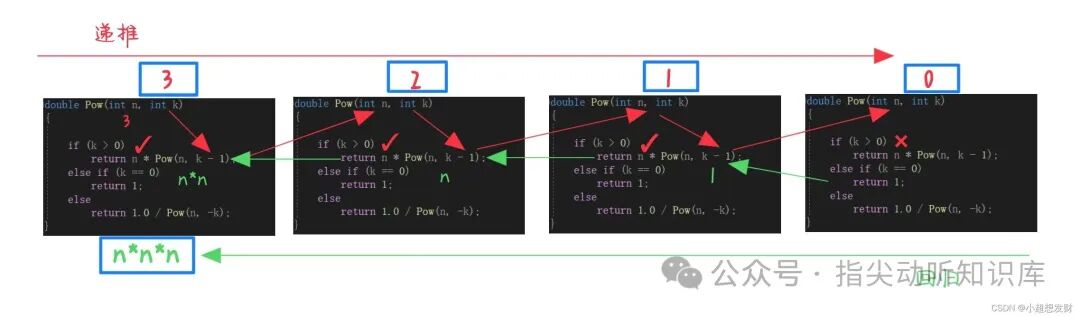
解题思路：需要考虑 k 为正数、零和负数的情况。以 k>0 和 k==0 为限制条件的核心。

• 当 k > 0 时：Pow(n, k) = n * Pow(n, k-1)，递归使 k 减小。
• 当 k == 0 时：任何非零数的0次幂为 1，这是递归出口。
• 当 k < 0 时：Pow(n, k) = 1.0 / Pow(n, -k)，转化为正指数幂的倒数。

n=3, k=3
Pow(3, 3) = 3 * Pow(3, 2)
Pow(3, 2) = 3 * Pow(3, 1)
Pow(3, 1) = 3 * Pow(3, 0)
Pow(3, 0) = 1

然后开始回归计算：1 -> 3*1=3 -> 3*3=9 -> 3*9=27。

代码实现：

double Pow(int n, int k)
{
    if (k > 0)
        return n * Pow(n, k - 1);  //①
    else if (k == 0)
        return 1;
    else
        return 1.0 / Pow(n, -k); //k是负数的时候，通过递归调用进入①分支
}

int main()
{
    int k = 0;
    int n = 0;
    scanf("%d %d", &n, &k);
    double ret = Pow(n, k);
    printf("%.1lf\n", ret);
    return 0;
}

3.4 字符串逆序

题目描述：
用递归方法实现字符串逆序（原地修改）。例如：输入字符串 "abcdef"，逆序后为 "fedcba"。

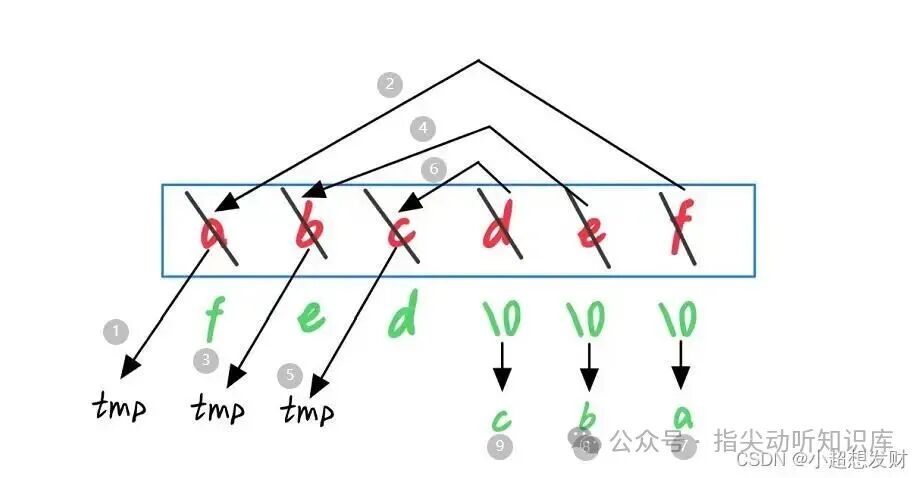
解题思路：这题需要以字符串（子串）的长度作为限制条件。策略是交换字符串首尾字符，然后对去掉首尾的中间子串进行递归。

1. 用临时变量 tmp 存储首字符 a。
2. 将尾字符 f 赋值给首字符位置。
3. 将尾字符位置置为 \0。这一步很关键，它确保了在下一步递归调用 strlen 时，计算的是去掉尾字符后的新子串长度。
4. 对新的子串（bcde\0）进行递归。
5. 递归回归后，再将暂存的 tmp（即原首字符 a）赋值到当前的尾字符位置。

通过递归，每次处理都向字符串中心推进，直到子串长度不大于1为止。

代码实现：

void reverse_string(char* string)
{
    int len = strlen(string); //计算当前（子）字符串长度
    char tmp = *string;
    *string = *(string + len - 1); //交换首尾字符
    *(string + len - 1) = '\0';    //将尾字符位置置为结束符，形成新的子串
    if(strlen(string+1) > 1 )      //如果剩余子串长度大于1，继续递归
        reverse_string(string + 1);
    *(string + len - 1) = tmp;     //递归返回后，将原首字符放到当前尾字符位置
}

int main()
{
    char arr[] = "abcdef";
    reverse_string(arr);
    printf("%s\n", arr); //输出 fedcba
    return 0;
}

3.5 斐波那契数

3.5.1 递归的实现

题目描述：
递归实现求第 n 个斐波那契数。斐波那契数列：1, 1, 2, 3, 5, 8, 13... (即 Fib(1)=1, Fib(2)=1, Fib(n)=Fib(n-1)+Fib(n-2), n>=3)。例如：输入 5，输出 5；输入 10，输出 55。

解题思路：根据定义直接翻译成递归代码。以 n<=2 为限制条件，此时返回 1。对于 n>2 的情况，Fib(n) 等于 Fib(n-1) 与 Fib(n-2) 之和，递归计算这两个子问题。这是理解动态规划思想的一个经典负面案例，因为纯递归解法效率极低。

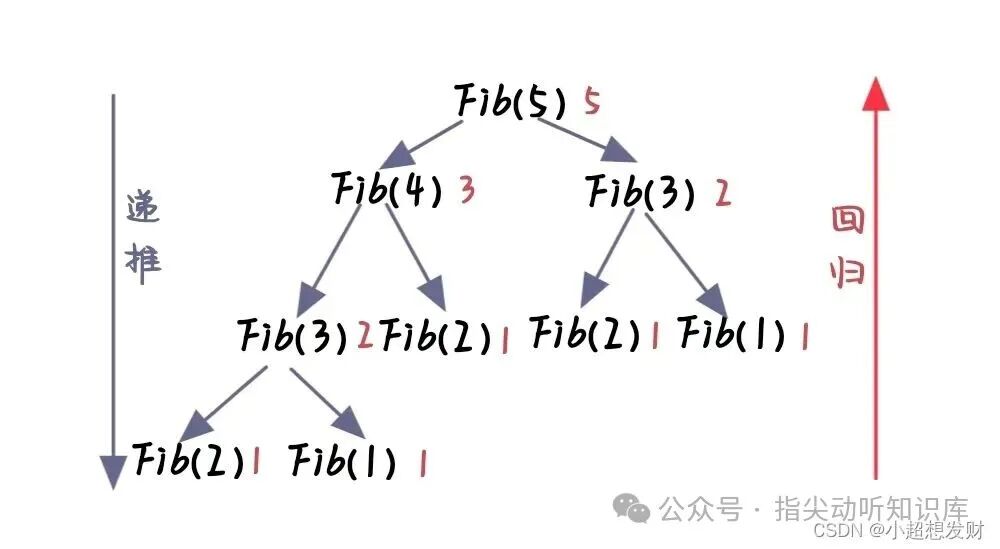
Fib(5)
= Fib(4) + Fib(3)
= (Fib(3)+Fib(2)) + (Fib(2)+Fib(1))
= ...

不断递推分解，直到所有分支都到达 Fib(1) 或 Fib(2)，然后开始回归求和。

代码实现：

long Fib(int n)
{
    if (n <= 2)
        return 1;
    else
        return Fib(n-1) + Fib(n-2);   //前两项加起来等于后一项
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    long ret = Fib(n);
    printf("%ld", ret);
    return 0;
}

3.5.2 非递归的实现

解题思路：为了避免递归的巨大开销，可以采用迭代（循环）方式。用三个变量滚动计算：n1 和 n2 存储前两个数，tmp 存储当前数。
初始 n1=1, n2=1。从第3项开始循环，每次循环中 tmp=n1+n2，然后更新 n1=n2, n2=tmp，同时 n--，直到处理完第 n 项。

代码实现：

int main()
{
    int n = 0;
    scanf("%d", &n);
    int i = 0;
    int n1 = 1;
    int n2 = 1;
    long tmp = 0;
    if (n == 1)
        printf("%d", 1);
    if (n == 2)
        printf("%d", 1);
    while (n>2)
    {
        tmp = n1 + n2;    //三项互相替换，迭代计算
        n1 = n2;
        n2 = tmp;
        n--;
    }
    printf("%ld", tmp);
    return 0;
}

递归 vs 非递归的效率分析：

• 递归的缺点在此例中暴露无遗。虽然“大事化小”的思路优雅，但计算 Fib(n) 时，会产生大量重复的函数调用分支，如上图所示的树形结构。每个函数调用都涉及压栈、传参、返回等开销。计算 Fib(40) 甚至 Fib(50) 时，等待时间将长得不切实际，这涉及到时间复杂度的指数级增长。
• 而非递归的迭代方法，只进行简单的循环，时间复杂度是线性的 (O(n))，空间复杂度是常数的 (O(1))，效率远高于递归版本。因此，对于斐波那契数问题，迭代实现是更优的选择。这也提醒我们，递归虽好，但需谨慎评估其性能成本。

3.6 经典问题之《青蛙跳台阶》

题目描述：
一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
例如：输入 5，输出 8。

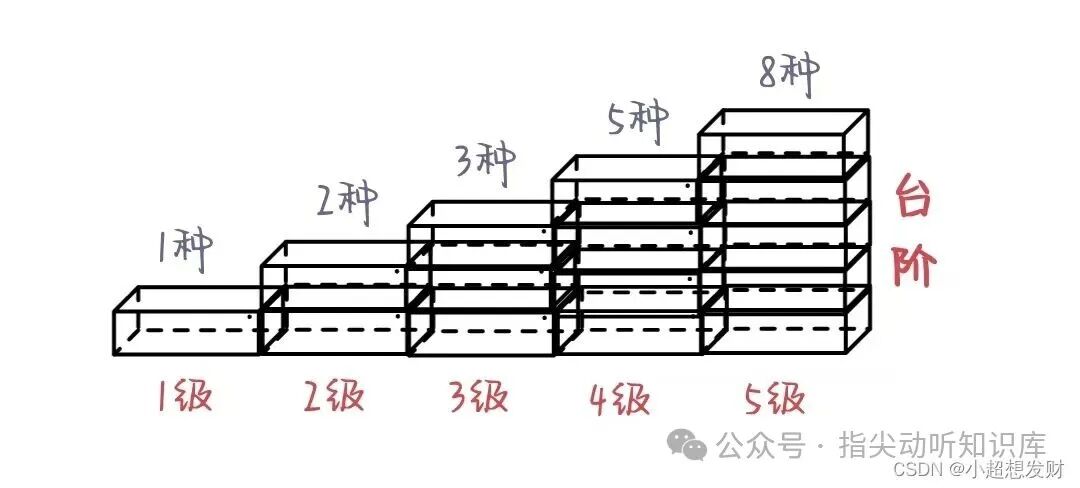
解题思路：青蛙跳台阶问题本质上就是斐波那契数列问题。我们可以分析：

• 跳1级台阶：有 1 种跳法。
• 跳2级台阶：有 2 种跳法 (1+1, 2)。
• 跳3级台阶：可以从第1级跳2步上来，也可以从第2级跳1步上来。所以跳法数 = (跳1级的方法数) + (跳2级的方法数) = 1+2=3。
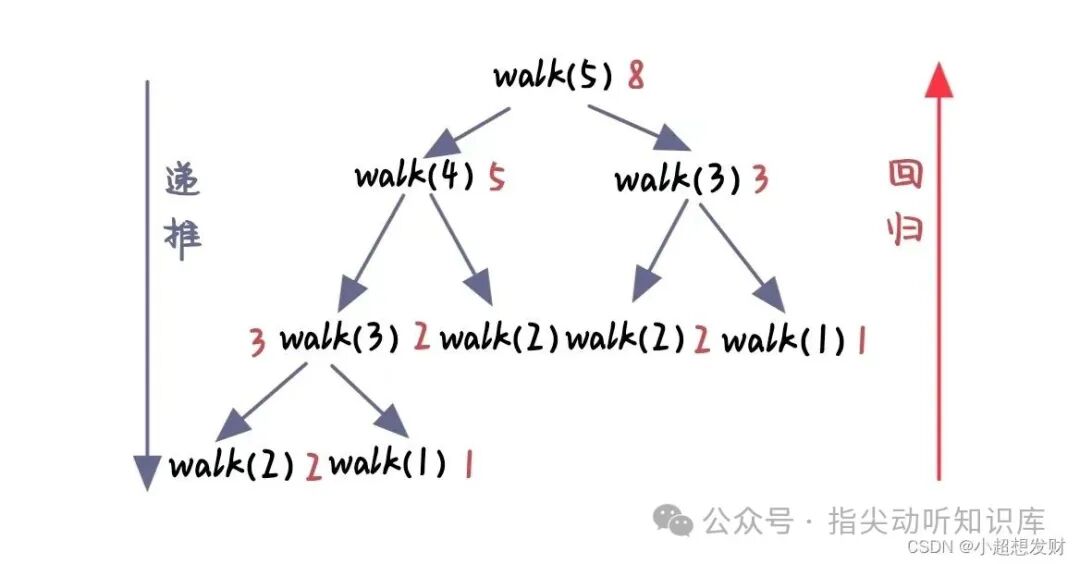
• 以此类推，跳 n 级台阶的方法数 walk(n) = walk(n-1) + walk(n-2)，其中 walk(1)=1, walk(2)=2。

这完全符合斐波那契数列的递推关系（只是初始项略有不同）。因此，问题转化为求解一个类斐波那契数列。

代码实现：

long walk(int n)
{
    if (n ==1)
        return 1;
    if (n ==2)
        return 2;
    else
        return walk(n-1) + walk(n-2);   //前两项加起来等于后一项
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    long ret = walk(n);
    printf("%ld", ret);
    return 0;
}

3.7 经典问题之《汉诺塔问题》

题目描述：
有三根柱子（A, B, C）。开始时，在A柱上从下往上按照大小顺序摞着 n 个圆盘。要求把所有圆盘按同样大小顺序重新摆放到C柱上。规则：

1. 每次只能移动一个圆盘。
2. 移动过程中，小圆盘上不能放大圆盘（即任何时刻，每根柱子上的圆盘都必须保持大盘在下，小盘在上）。

解题思路：这是递归思想的终极体现之一，必须采用大事化小的策略。我们不需要（也最好别去）深究每一步的具体移动过程，而应理解递归框架。

假设函数 Plate_Move(n, A, B, C) 表示将 n 个盘子从 A 柱（起点），借助 B 柱（中转），移动到 C 柱（终点）。

1. 递归出口 (n==1)：如果只有一个盘子，直接将它从 A 移到 C。
2. 递归步骤 (n > 1)：
   • 先将 A 柱上面的 n-1 个盘子，借助 C 柱，移动到 B 柱上。即 Plate_Move(n-1, A, C, B)。
   • 此时 A 柱只剩下最大的第 n 个盘子，将它直接移动到 C 柱。即 Move(A, C)。
   • 最后，将 B 柱上的 n-1 个盘子，借助 A 柱，移动到 C 柱上。即 Plate_Move(n-1, B, A, C)。

代码实现：

void Move(char src, char dest)
{
    // src表示起始柱，dest表示目标柱
    printf("盘子从%c柱子->%c柱子\n", src, dest);
}

void Plate_Move(int n, char A, char B, char C)
{
    if (n == 1)
    {
        Move(A, C);   //递归出口：只剩一个盘子，直接移动
    }
    else
    {
        Plate_Move(n-1, A, C, B); //步骤1：将n-1个盘子从A借助C移到B
        Move(A, C);               //步骤2：将最大的盘子从A移到C
        Plate_Move(n-1, B, A, C); //步骤3：将n-1个盘子从B借助A移到C
    }
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    Plate_Move(n, 'A', 'B', 'C');  //n为圆盘数，A是起始柱，B是中转柱，C是目标柱
    return 0;
}

过程演示：

(1) A柱上有1个圆盘：

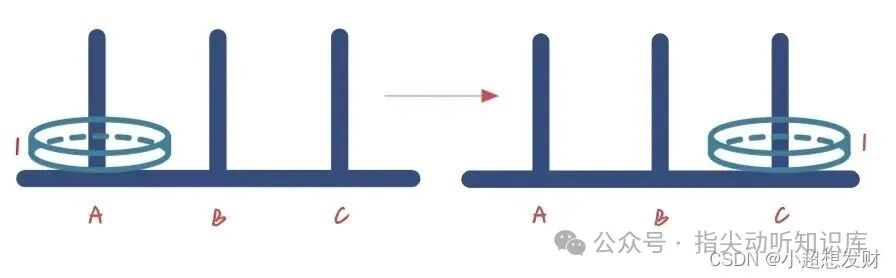
(2) A柱上有2个圆盘：

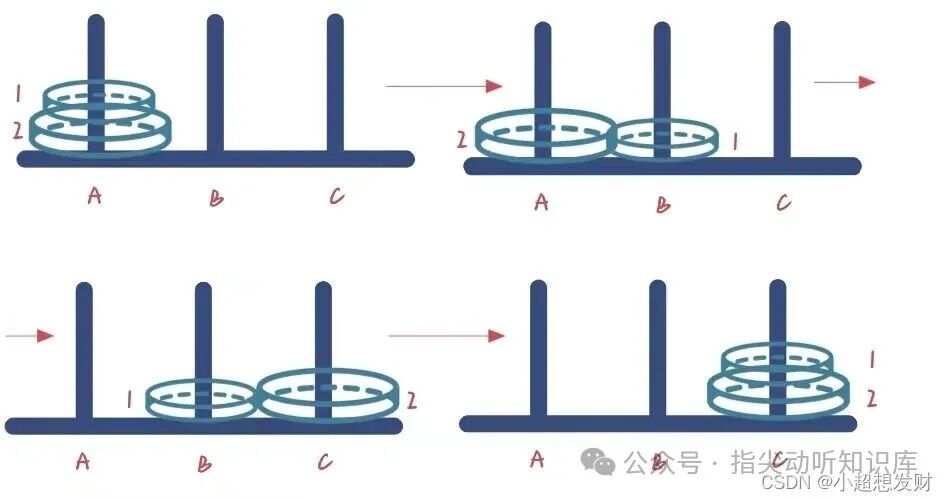
(3) A柱上有3个圆盘：

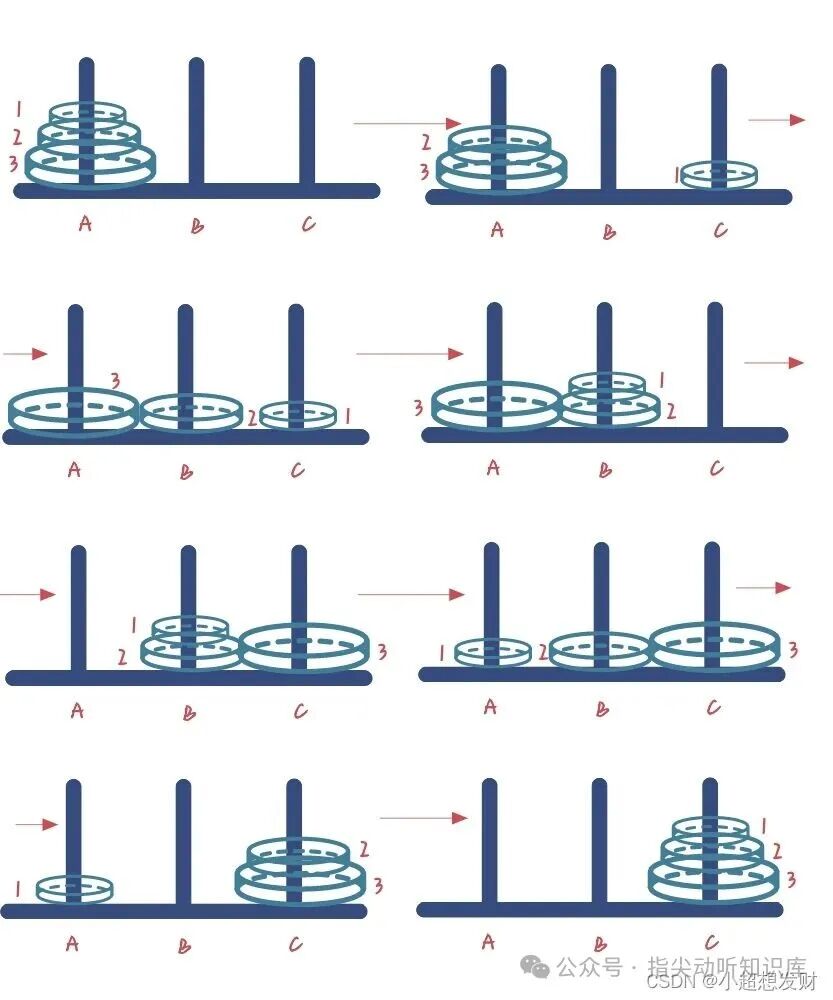
(4) A柱上有n个圆盘的通用递归思路：

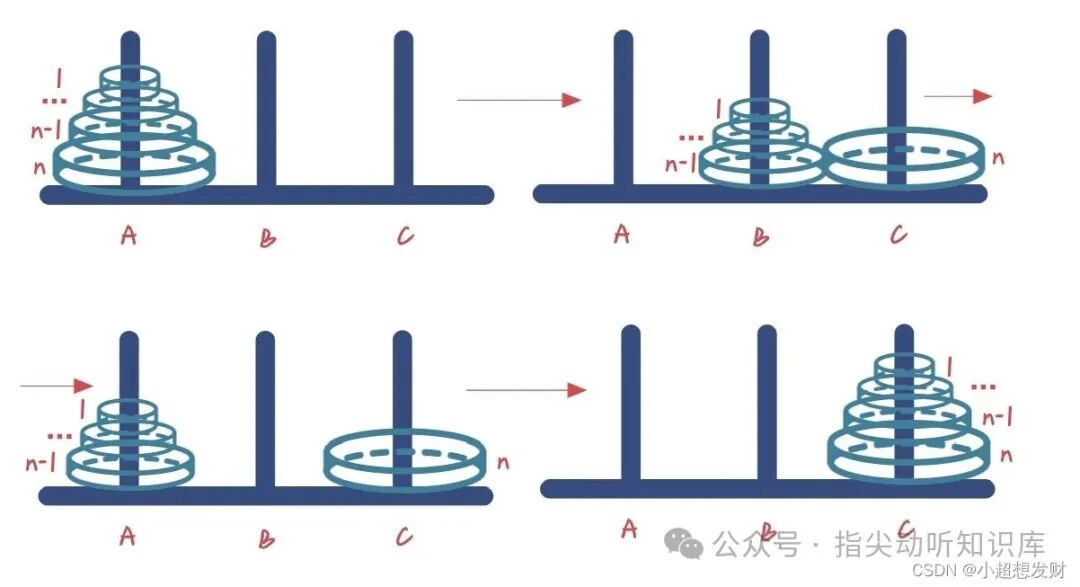
递归是C语言乃至整个计算机科学中一种强大而精妙的编程思想。它用简洁的代码描绘了复杂的过程，但其性能和栈空间消耗是需要时刻警惕的。掌握递归的关键在于清晰地定义“递归出口”和“递归体”，并信任递归能正确地处理子问题。从打印数字到解决汉诺塔，递归展现出的“分而治之”的威力，是每个程序员工具箱中不可或缺的利器。希望本文的讲解和示例能帮助你更好地理解与运用递归。如果你想深入探讨更多C/C++的底层细节或算法优化，欢迎在云栈社区继续交流。