Python实现机械振动信号的相位无关特征提取：频域解耦与低秩近似

本文介绍一种用于机械振动信号分析的相位无关型二维特征表征算法。该算法的核心是将一维振动信号转换为一个具有相位不变性的二维特征矩阵（FRGM），从而为基于深度学习的故障诊断模型提供稳定、高信息密度的输入。

核心算法流程

整个处理流程旨在消除原始信号的相位影响，并实现不同长度信号在特征空间的一致性表示。其主要步骤如下图所示，后文将逐一详解。

开始
↓
输入一维振动信号
↓
快速傅里叶变换（FFT）到频域
↓
提取正频率复数序列
↓
构建实部-虚部二维矩阵
↓
矩阵去中心化处理
↓
计算协方差矩阵
↓
特征值分解获取变换矩阵
↓
实部与虚部解耦变换
↓
构建格拉姆矩阵（向量内积）
↓
奇异值分解（SVD）
↓
低秩近似截断
↓
输出FRGM特征矩阵
↓
结束

算法详细步骤解析

第一步：频域转换
对输入的原始一维时域振动信号进行快速傅里叶变换（FFT），将其转换到频域，获得包含幅度和相位信息的复数序列，为后续的相位解耦处理奠定基础。

第二步：正频率提取
从完整的傅里叶变换结果中提取正频率部分对应的复数序列。这一步去除了冗余的负频率信息，在降低数据维度的同时，完整保留了信号的特征信息。

第三步：实虚部分离与矩阵构建
将上一步得到的复数序列分离为实部（对应余弦分量）和虚部（对应正弦分量）两个分量，并将它们组合成一个2行N列的二维矩阵，完成从一维序列到二维结构的初步转换。

第四步：中心化处理
分别计算实部和虚部分量的均值，并对矩阵进行去中心化操作。这一步消除了信号中可能存在的直流偏移影响，使数据围绕零值分布，为后续的协方差分析做好准备。

第五步：协方差分析
计算去中心化后实部与虚部两个分量之间的协方差矩阵。该矩阵量化了二者之间的线性相关程度，揭示了信号内在的统计特性。利用Python的科学计算库（如NumPy）可以高效完成此类矩阵运算。

第六步：特征解耦
对协方差矩阵进行特征值分解，获得其特征向量和特征值。利用这些特征向量构造一个线性变换矩阵，对原始的实部-虚部矩阵进行变换，从而实现实部与虚部的解耦，消除它们之间的线性相关性。

第七步：格拉姆矩阵构建
将解耦后的复数序列中的每个频率点视为一个二维向量，计算所有向量对之间的内积，从而形成一个对称的格拉姆矩阵。这个矩阵记录了所有向量之间的相似性关系。

第八步：低秩近似
对格拉姆矩阵进行奇异值分解（SVD）。根据预设的能量贡献率（例如保留95%的能量），截断较小的奇异值及其对应的向量，用一个低秩矩阵来近似原始的格拉姆矩阵。这一步实现了特征压缩和噪声抑制，是算法降维的核心。

第九步：归一化与输出
对得到的低秩近似矩阵进行归一化处理（如最大-最小归一化），将数值范围调整到合理的区间（如[0,1]），最终生成标准的FRGM二维特征矩阵，可直接作为卷积神经网络（CNN）等深度学习模型的输入。

算法效果示意

以下示意图展示了算法处理振动信号的关键步骤与结果：

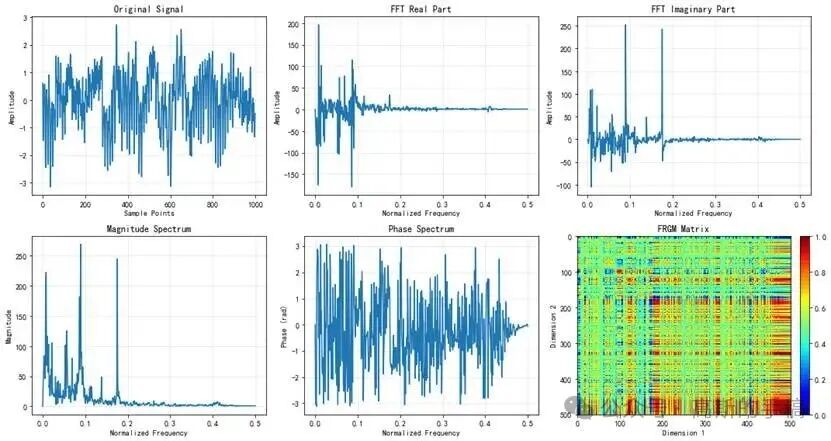
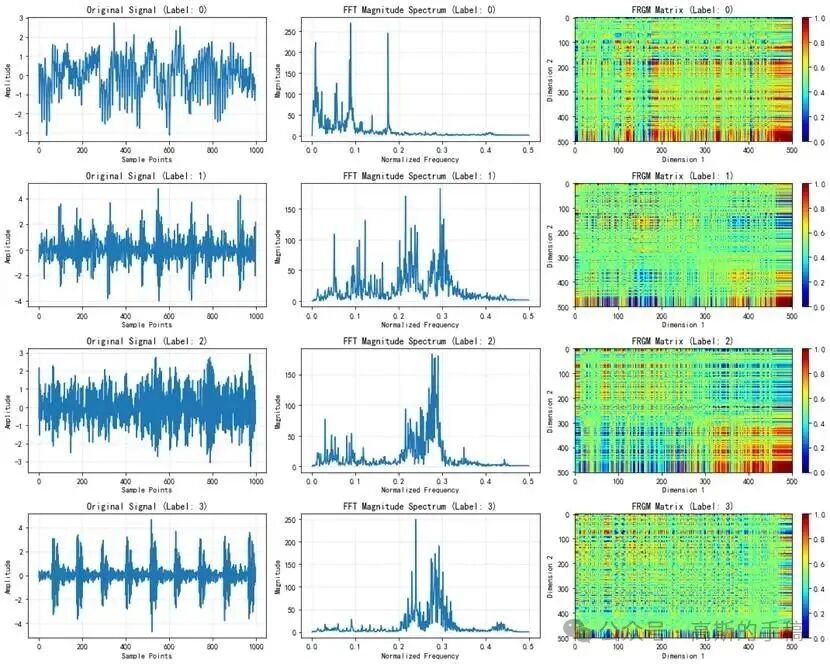
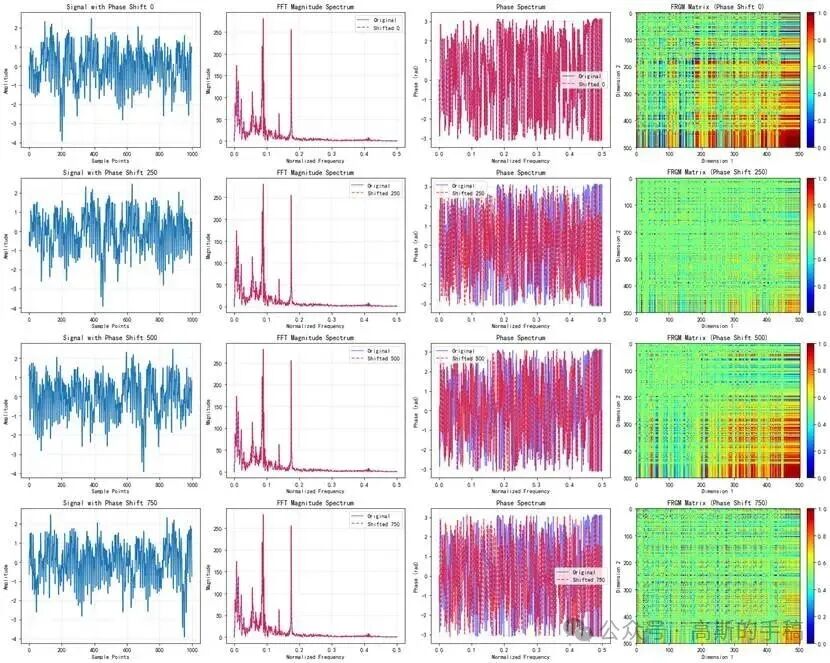
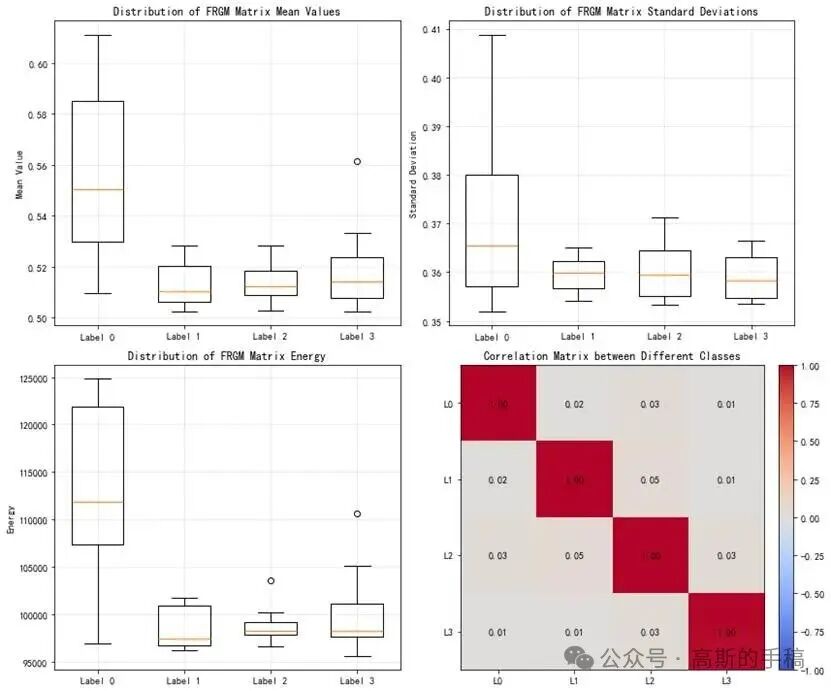
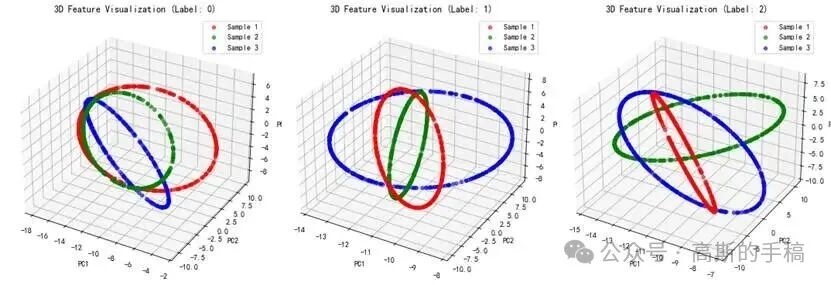
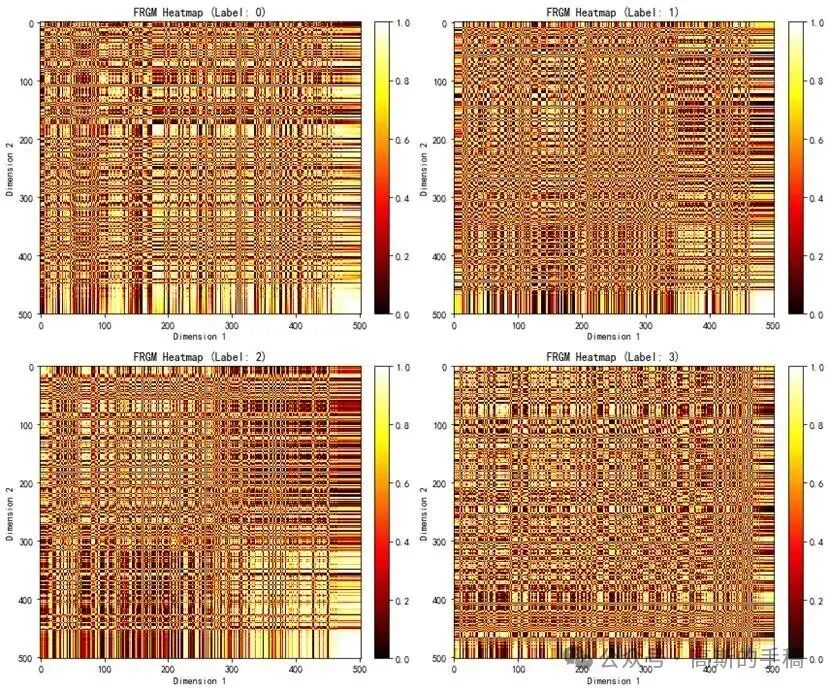
代码实现

算法的完整Python实现代码已整理，你可以通过以下链接查看和获取：
完整代码实现