
无论是全球气候的演变、传染病的蔓延、金融市场的震荡,还是大脑的认知活动,这些复杂的系统都由海量的组件构成,组件之间存在着多样且动态的相互作用。由于这些相互作用具有非线性、涌现性、自适应性等特征,系统的集体行为往往难以用简单的还原论方法进行预测。面对这些错综复杂的涌现现象,科学家们亟需一套强大而普适的数学语言来对其进行描述、量化和深入理解。
起源于通信领域的信息论,因其能够跨越不同领域,精确定量地描述组件之间、系统与环境、整体与部分之间的互动,正逐渐成为复杂系统研究中不可或缺的分析工具。本文基于对综述文章《Information theory for complex systems scientists: What, why, and how》的解读,系统阐述信息理论为何能成为复杂系统科学的基石,并详解其核心概念、进阶工具与实际应用场景。

一、 信息理论的基石:核心概念与直觉构建
文章首先详细讲解了信息理论的几个核心度量指标,其中最基础的概念无疑是熵。据说香农在提出信息论后,曾请教冯·诺依曼该如何命名这个新的不确定性度量。冯·诺依曼的回答是:“你应该称之为熵,因为没人真正知道熵是什么,这样你在辩论中总是占上风。” 这个故事恰恰说明,尽管香农最初的定义聚焦于通信,但他所构建的数学框架具有高度的通用性和多种解读可能。
1.1 熵:不确定性的量化
设想一个天气预报的场景。如果某地一年365天都是晴天,那么你对“明天天气”的不确定性为零,熵也为零。如果天气晴朗和下雨的概率各占50%,你的不确定性最大,熵也达到最高值。因此,熵本质上是衡量我们在得知具体结果之前,对一个随机变量各种可能取值的“惊讶”程度的期望值。
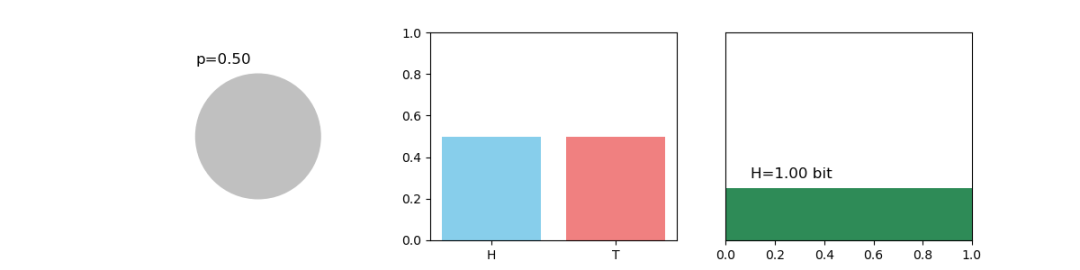
图1:信息熵示意图,不同概率分布对应不同的熵值
对于一个离散随机变量X,其香农熵H(X)的数学定义为:
H(X) = -Σ p(x) log p(x)
其中 p(x) 是 X 取值为 x 的概率。对数的底数通常取2,此时熵的单位是比特。
应用示例:
- 在神经科学中,一个神经元放电序列的熵可用于衡量其响应的变异性。
- 在生态学中,一个物种空间分布模式的熵可以反映其分布的不确定性。
- 在金融学中,一只股票价格时间序列的熵可以表征其波动性。
1.2 联合熵与条件熵
联合熵 H(X, Y) 衡量的是两个随机变量X和Y联合分布的总不确定性。它总是大于或等于单个变量的熵,但小于或等于两者熵之和。
条件熵 H(Y|X) 表示在已知随机变量X取值的情况下,对随机变量Y仍然存在的不确定性。如果X和Y完全独立,则 H(Y|X) = H(Y);如果Y完全由X决定,则 H(Y|X) = 0。
一个关键的关系式是:
H(X, Y) = H(X) + H(Y|X)
这直观地表明,X和Y的总不确定性,等于X自身的不确定性,加上在已知X后Y所剩余的不确定性。
1.3 互信息:依赖关系的纯粹度量
互信息 I(X;Y) 是信息理论中的核心度量,堪称“皇冠上的明珠”。它衡量的是,通过观察一个变量X,我们平均能获得关于另一个变量Y的信息量。换言之,它量化了X和Y之间的统计依赖性,其范围从0(完全独立)到 min(H(X), H(Y))(完全依赖)。
I(X;Y) = H(X) + H(Y) - H(X, Y)
这个公式表明,变量X和Y之间的互信息,等于它们各自不确定性的总和,减去它们的联合不确定性。被“抵消”掉的那部分不确定性,正是由X和Y所共享的信息。
与仅能捕捉线性关系的皮尔逊相关系数不同,互信息能捕捉任何形式的统计依赖,包括非线性和非单调的关系。例如,在 Y = X² 的关系中,相关系数可能为0,但互信息值会很高。
应用示例:
- 在脑网络中,可以用互信息连接两个脑区,量化它们神经活动的同步性。
- 在基因调控网络中,可以连接两个基因,表示其表达水平的协同变化。

图2:互信息的拆解示意图
1.4 相对熵(Kullback-Leibler散度)
相对熵 D_KL(p || q) 用于衡量两个概率分布p和q之间的差异(严格来说它不对称,因而不是距离)。它量化了当真实分布为p时,使用分布q来近似所造成的信息损失。
有趣的是,互信息可以表示为一种特殊的相对熵:
I(X;Y) = D_KL( p(x,y) || p(x)p(y) )
从上述等式可以看出,互信息衡量的是X和Y的联合分布p(x,y)与它们假设独立时的分布乘积p(x)p(y)之间的“差异”。差异越大,说明它们越不独立,共享的信息越多。
例如,考虑投掷一个正常的骰子和一个有偏的骰子这两个独立事件,投掷五次时,两个事件分布的相对熵变化如下图所示:
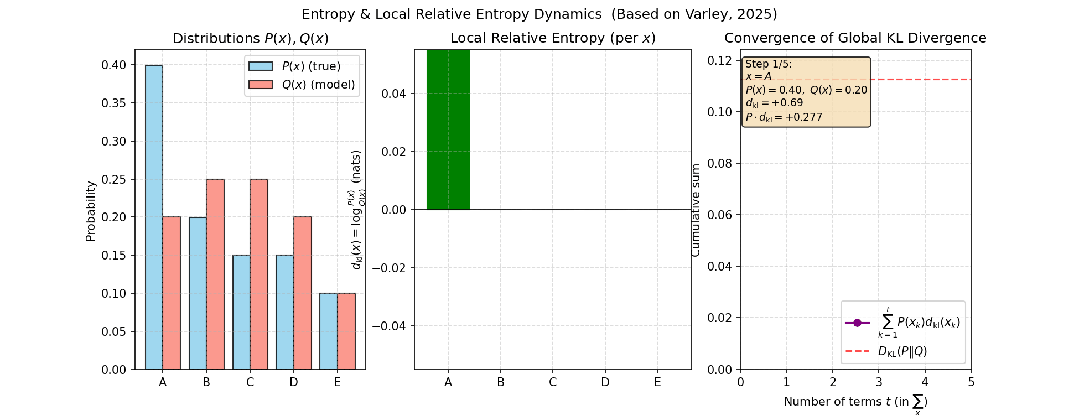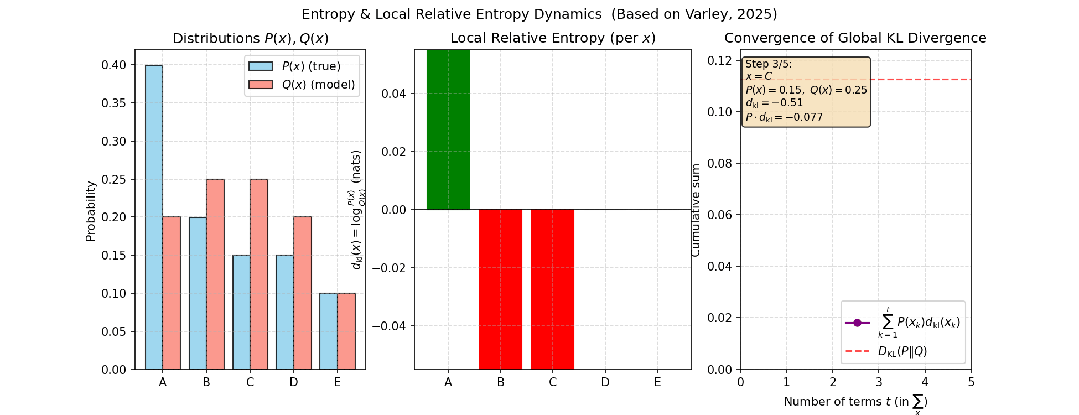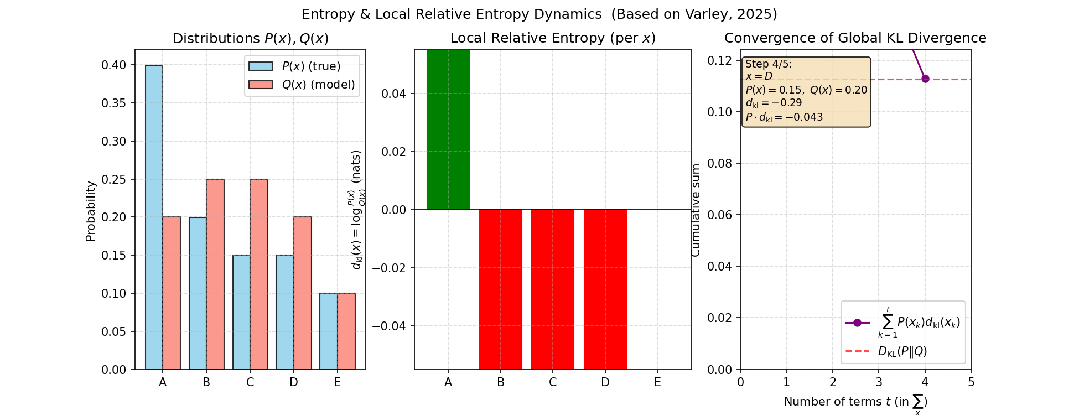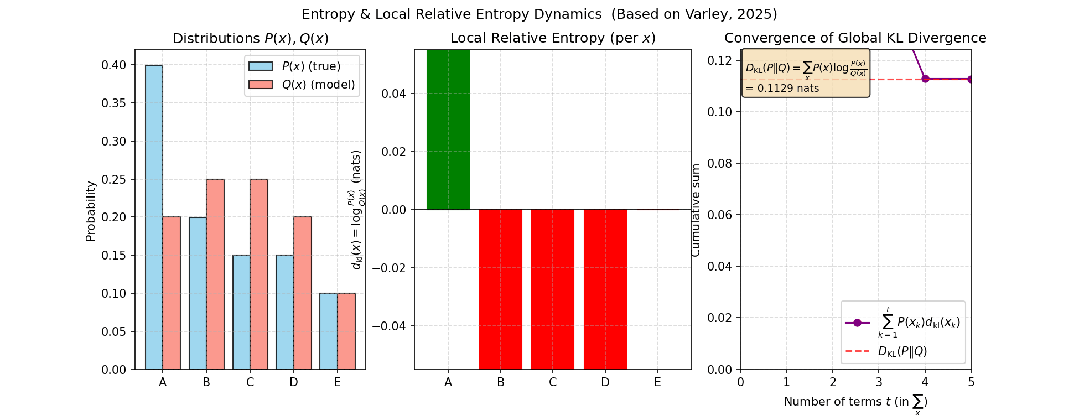
图3:投掷正常骰子与有偏骰子五次,其分布间相对熵的变化过程
基础的信息度量(如互信息)如同给复杂系统拍了一张静态照片,它能显示哪些节点之间有连接,但无法揭示信息是如何在这些连接中流动的,也无法解析这些连接背后更深层的结构。接下来要介绍的动态指标,会将这张静态照片升级为一部动态的、可解构的“4D电影”。
二、信息论如何直接描摹复杂系统的动态特征
复杂系统中,信息的传递是动态且随时间演化的。信息动力学旨在量化信息在系统内部及与环境之间的产生、存储、传递和修改。
2.1 传递熵
传递熵由Thomas Schreiber提出,是互信息在时间序列上的推广。它衡量的是,在已知变量Y自身过去历史的情况下,变量X的过去历史能为预测Y的当前状态提供多少额外的信息,即定向的信息流。
例如,在神经科学中,传递熵可用于推断脑区A的活动是否影响脑区B,从而判断因果关系的方向,这比仅进行非方向性量化的格兰杰因果检验更为强大。
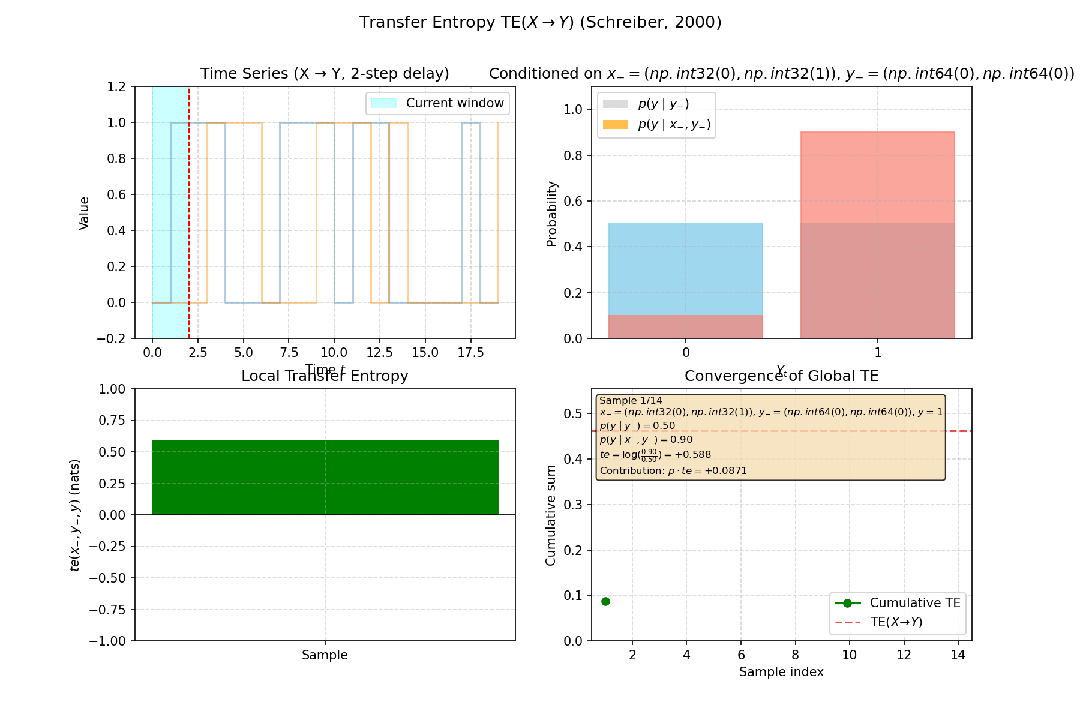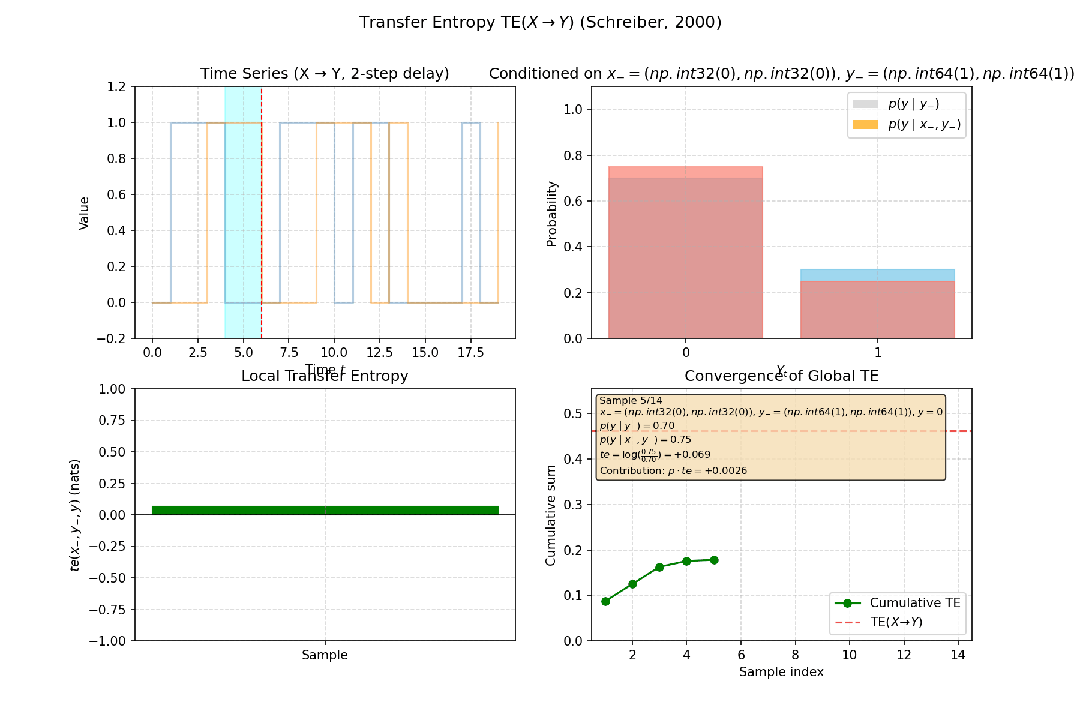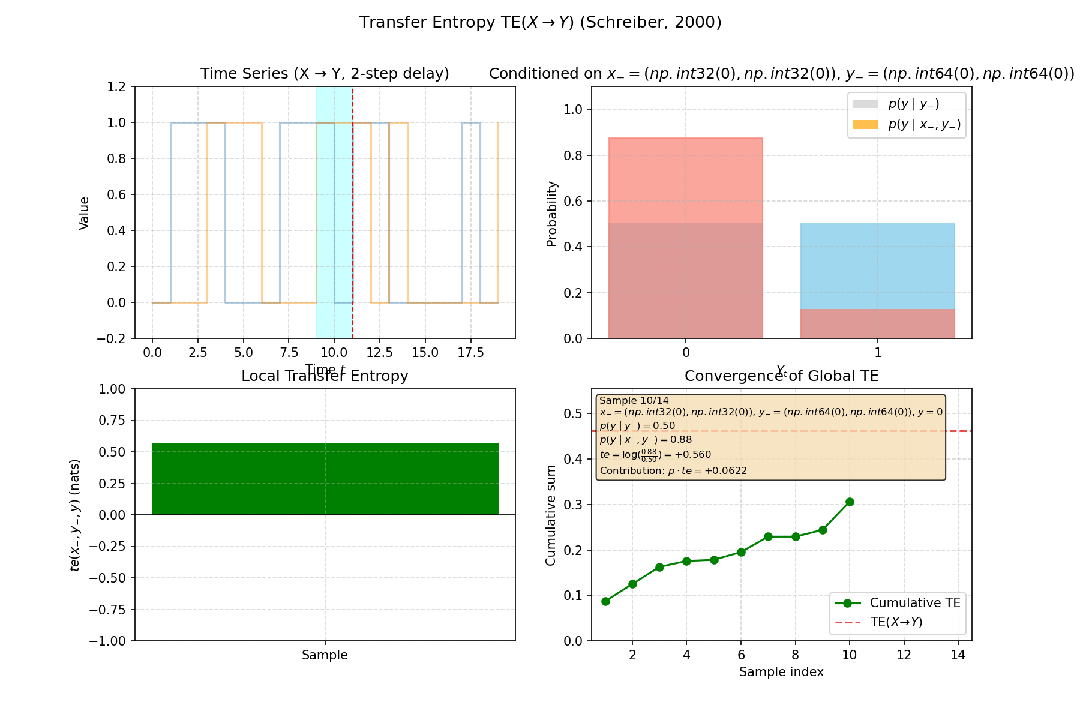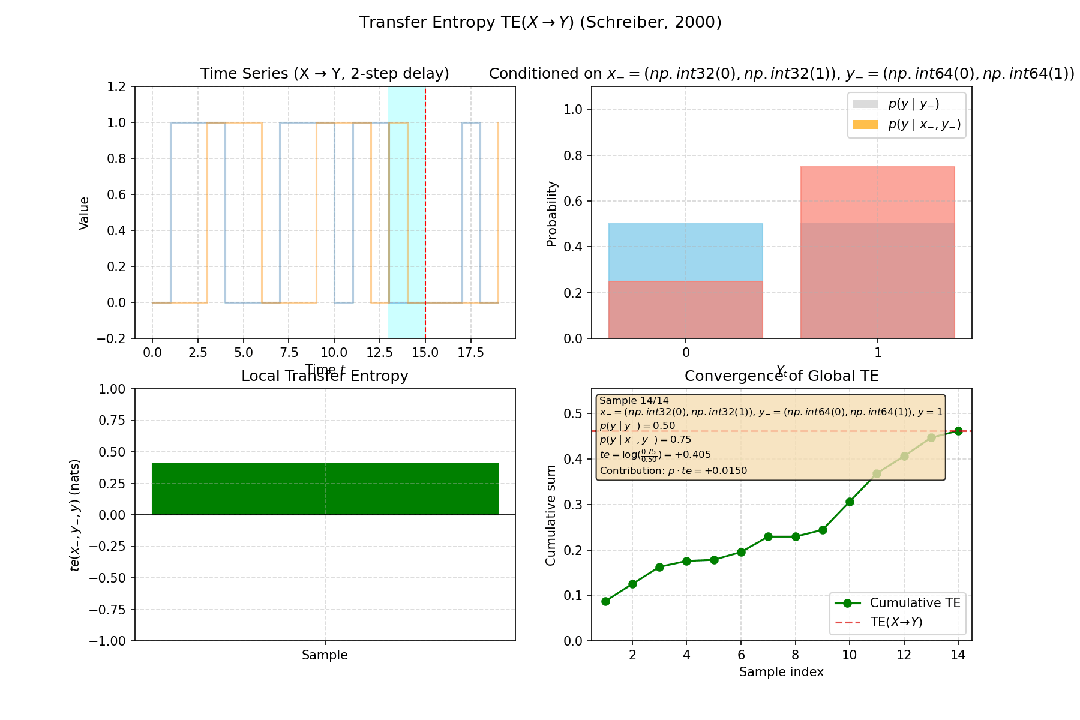
图4:构造一个简单因果系统:Yt = X{t-2} ⊕ Noise (X 以 2 步延迟影响 Y),X到Y的传递熵为正值,说明是X影响Y
2.2 主动信息存储
主动信息存储(AIS) 衡量一个系统组成部分的过去历史中,有多少信息与其当前状态相关。这量化了系统内部记忆或信息存储的能力。一个具有高AIS的单元,其行为在很大程度上由其自身的历史决定。
应用分析:
- 混沌时间序列:混沌系统是确定性的,但由于对初始条件极端敏感(蝴蝶效应),其短期历史对预测当前状态很有价值,但长期历史的预测价值会迅速衰减。因此,设定一个适当的时间窗口(如10步)时,计算出的AIS会是中等偏高的值,表明系统在短期内有“记忆”。
- 金融市场:有效市场假说认为,股价历史不能预测未来,收益率序列接近随机游走。如果计算出的AIS值非常低(接近零),则意味着资产的过去价格对其当前价格几乎没有提供额外信息,支持“市场无记忆”的观点。反之,若某只股票的AIS持续较高,则可能暗示存在可预测的模式。
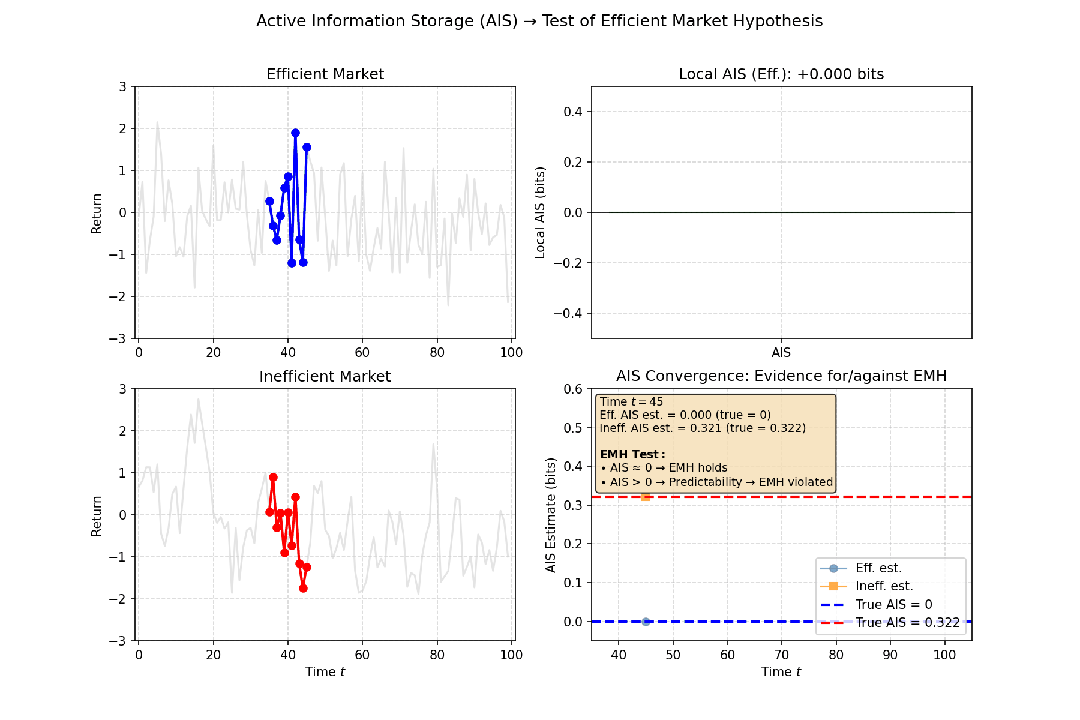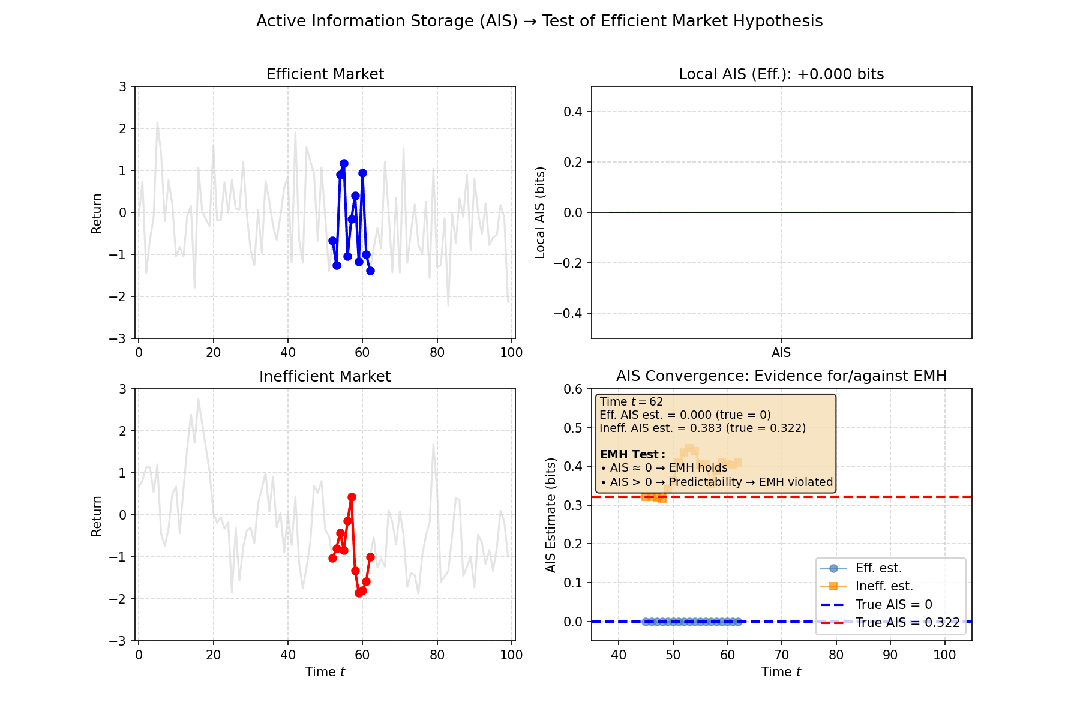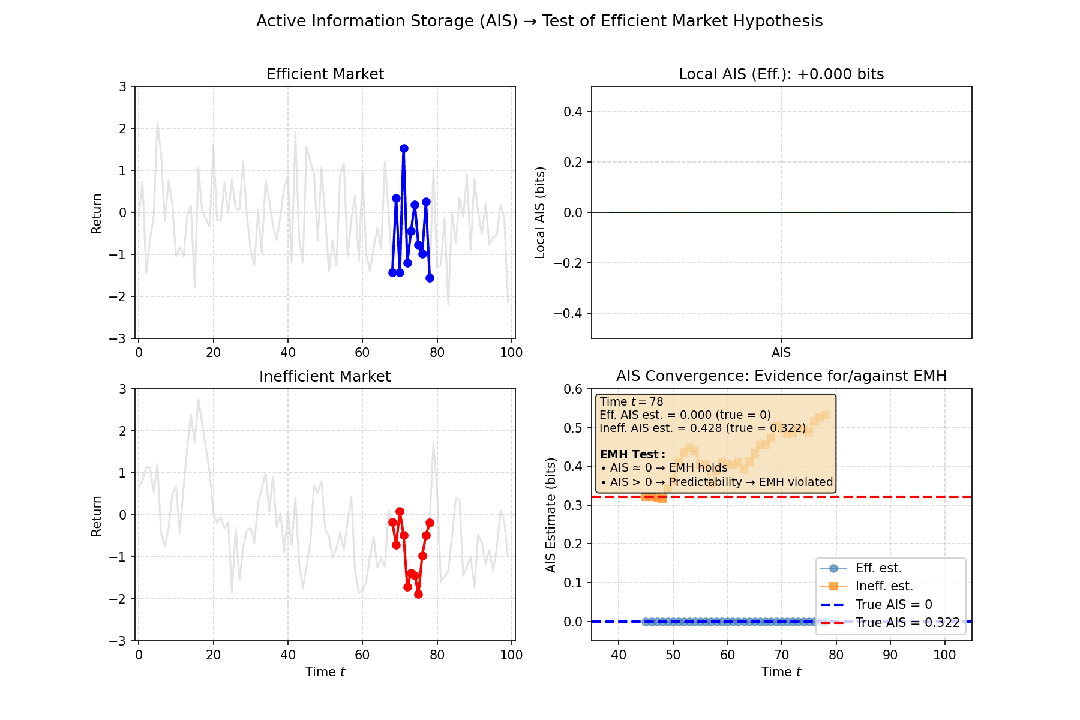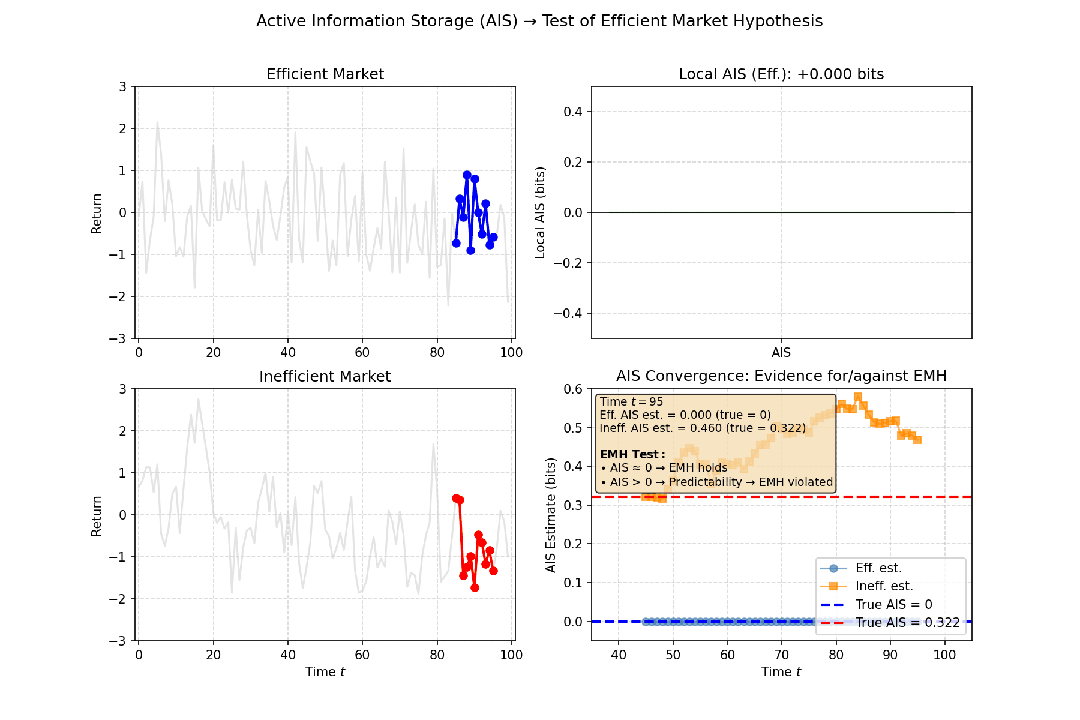
图5:满足与不满足有效市场假说的场景下,对应的主动信息存储值不同
2.3 整合信息论
整合信息论(IIT) 由神经科学家Giulio Tononi提出,试图用量化指标度量意识。其核心思想是:一个系统的“意识”程度,取决于其各个部分整合信息的程度,即整个系统所产生的信息大于其各部分信息之和的程度。
思想实验对比:
- 高分辨率数码相机:由数百万个光电管组成,每个像素都能高保真记录光信息,整个传感器接收的信息量巨大。但是,传感器各部分(像素)之间几乎没有因果相互作用(一个像素的状态不影响相邻像素)。如果将传感器切成两半,每一半仍能独立工作。因此,这个系统的整合信息Φ非常低,故相机不可能有意识体验。
- 大脑:不同脑区以极其复杂的方式相互作用。视觉信息需要与记忆、情感、语言等区域整合,才能形成“看到一朵红玫瑰”这样统一、不可分割的体验。如果大脑不同区域联系减弱(如裂脑症),这种统一体验就消失了。因此,大脑作为一个整体的信息远超其部分信息之和,其整合信息Φ被认为非常高。
整合信息论将Φ与意识的度量直接关联,但最大的挑战在于Φ的计算对于像大脑这样的系统极其困难,因此该理论在学界存在巨大争议。
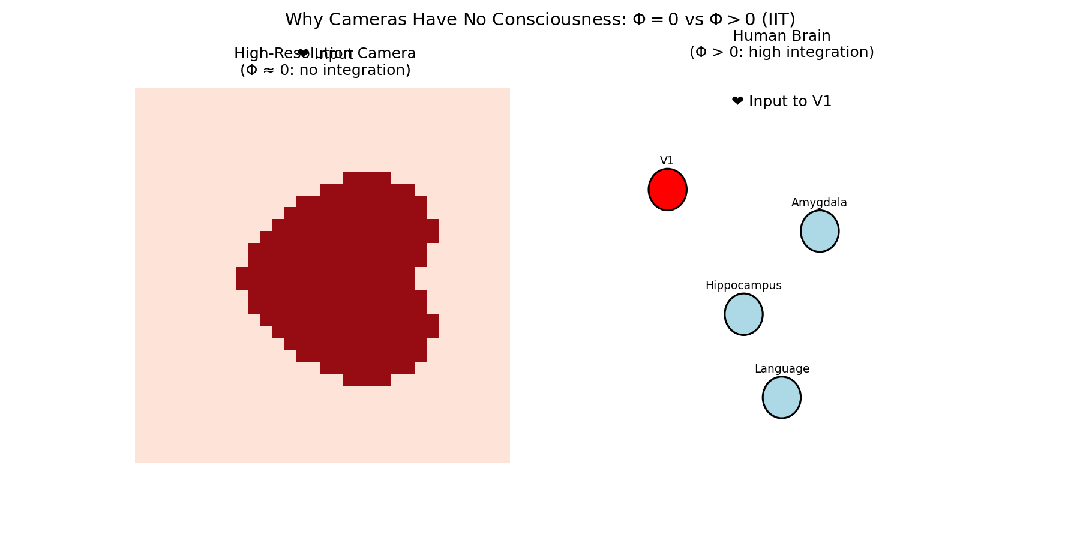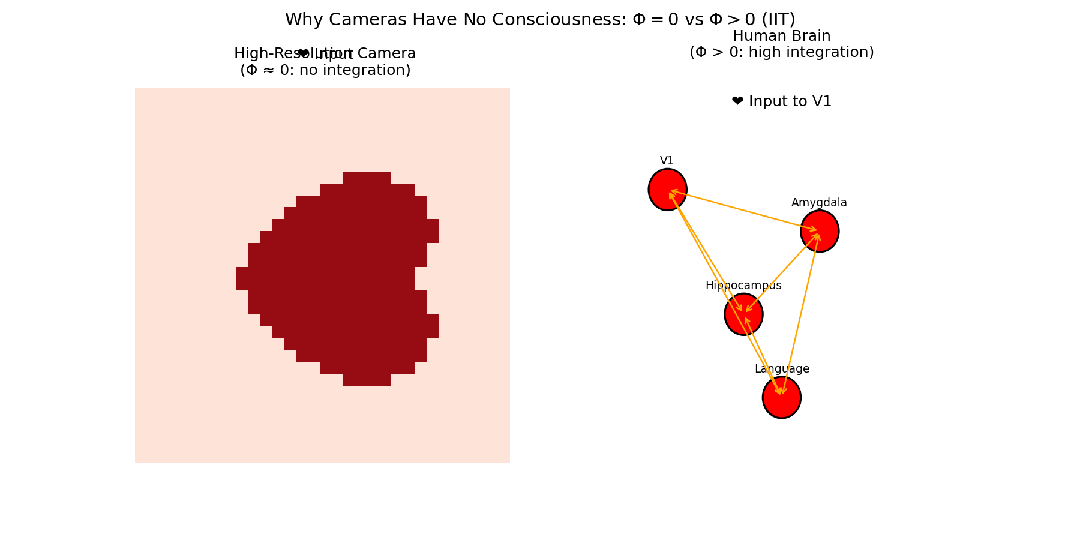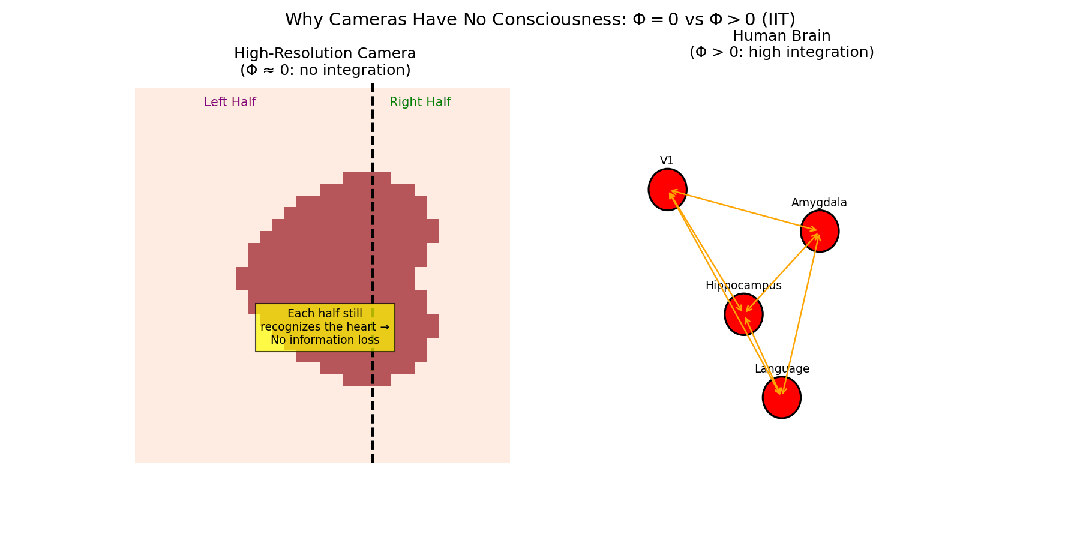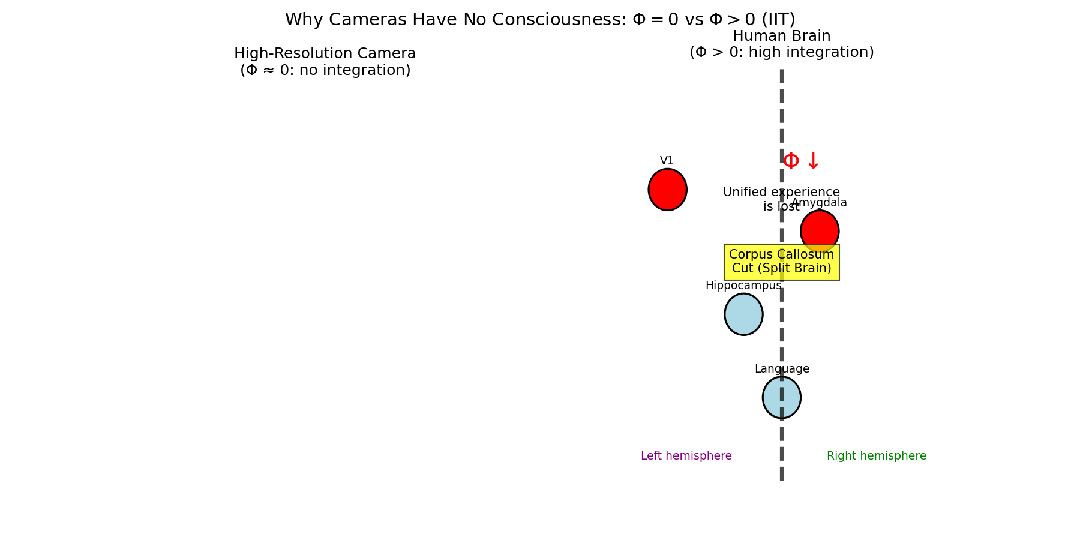
图6:对比照相机和大脑在视觉处理上的信息整合程度
2.4 统计复杂性与因果态
通过分析时间序列的历史数据,可以将所有能预测相同未来状态的历史归入同一个“因果态”。这是对系统动态过程的一种最优压缩表示。
统计复杂性是这些因果态分布的熵。它衡量了系统为了准确预测未来,必须记住多少关于过去的信息,即系统为生成观测到的时间序列,其内部所需的最小记忆量。一个具有中等统计复杂性的系统,通常具有丰富的内部结构和动态模式。
以观测萤火虫闪光序列为例:亮、暗、亮、亮、暗……初看随机。但如果某些“历史模式”(如“亮-暗”)总是预测下一刻“亮”,而另一些(如“暗-暗”)总导向“暗”,那么这些历史就应被归为两类——它们虽细节不同,却对未来有相同的预测效力。
这些具有相同预测效力的历史,就被归并为一个因果态节点。由这些因果态构成的最小、最简、最优预测器被称为 ϵ-机器。无论是统计复杂性的最优压缩,还是ϵ-机器的内在状态结构,都说明了复杂系统之所以复杂,在于其内在状态结构的不可简约性。
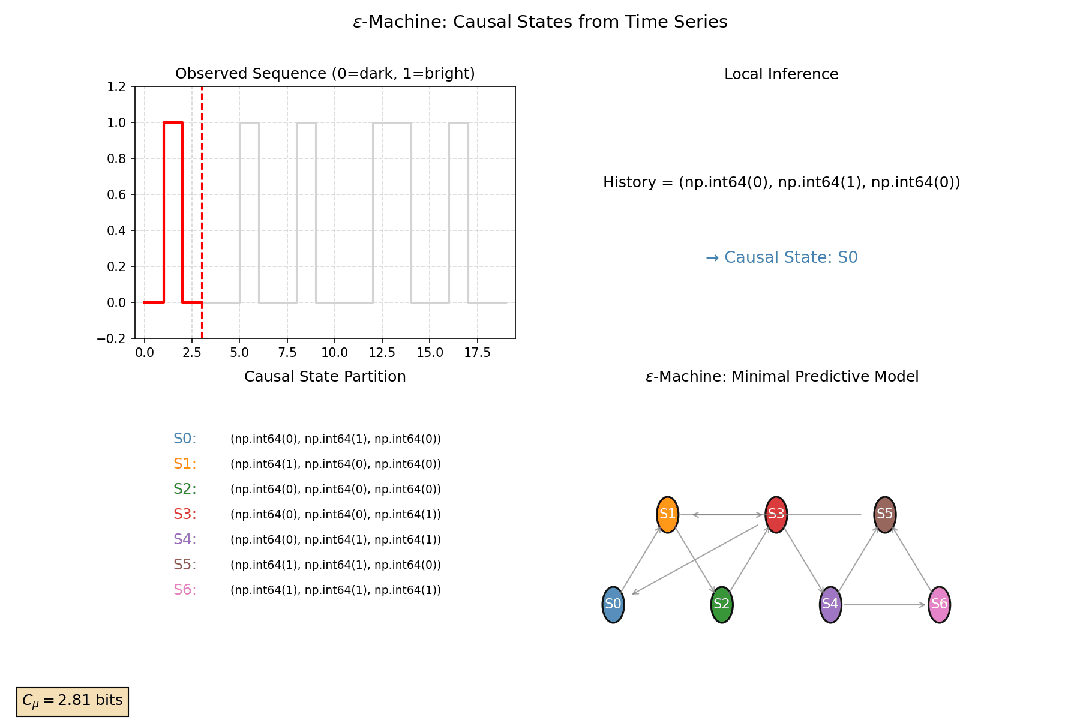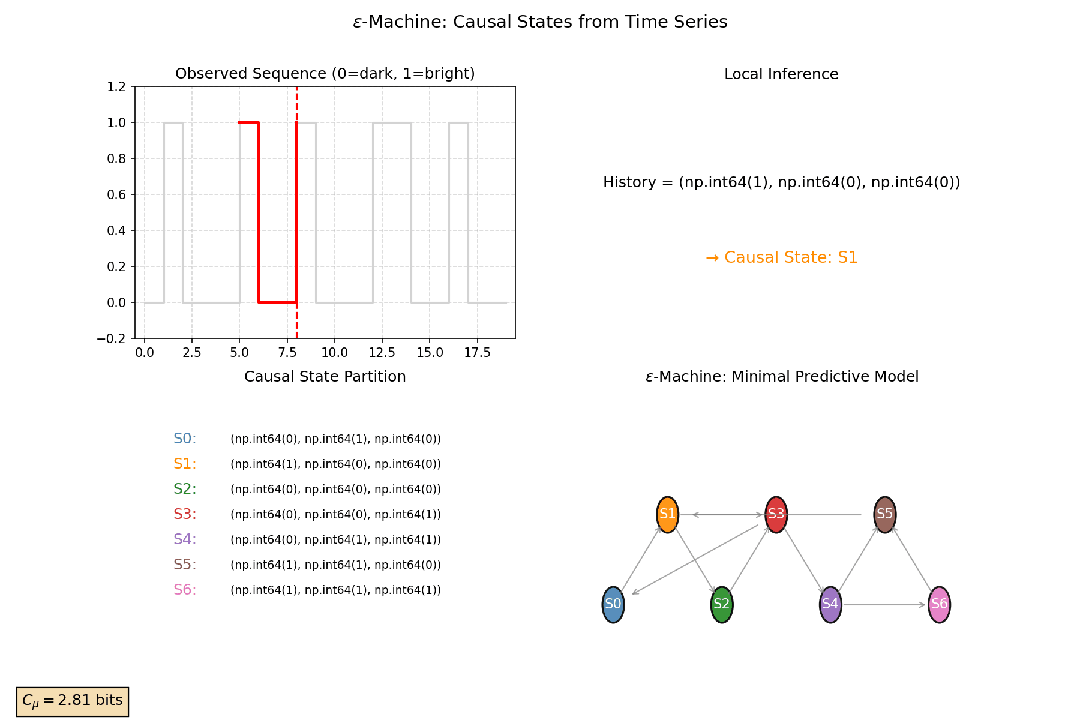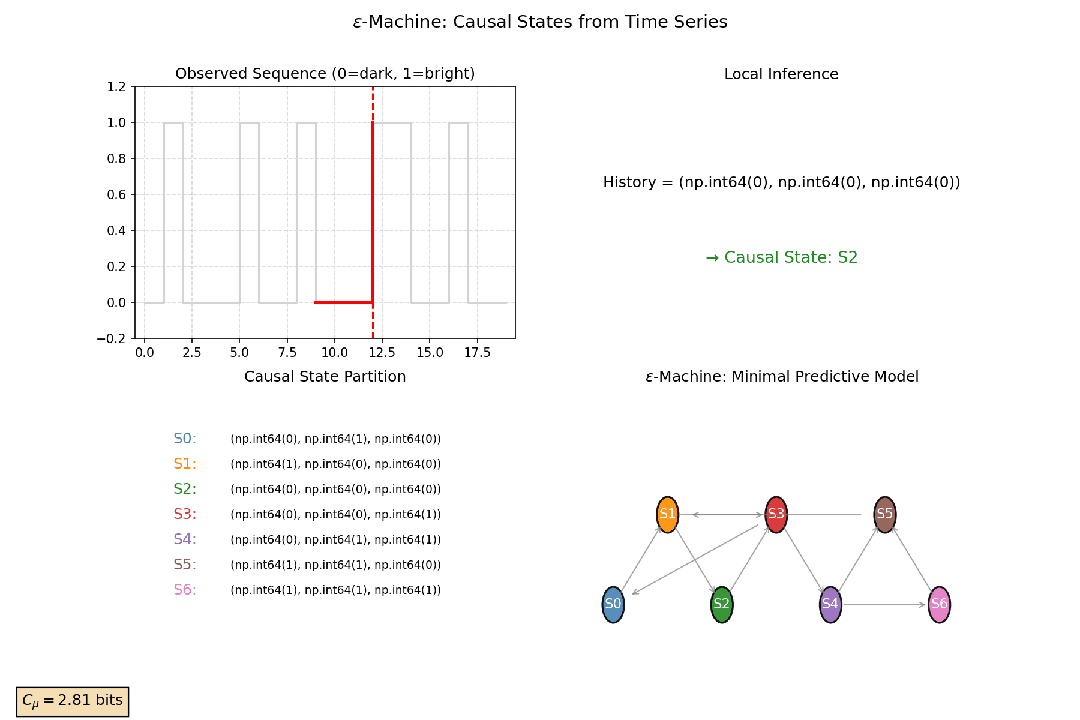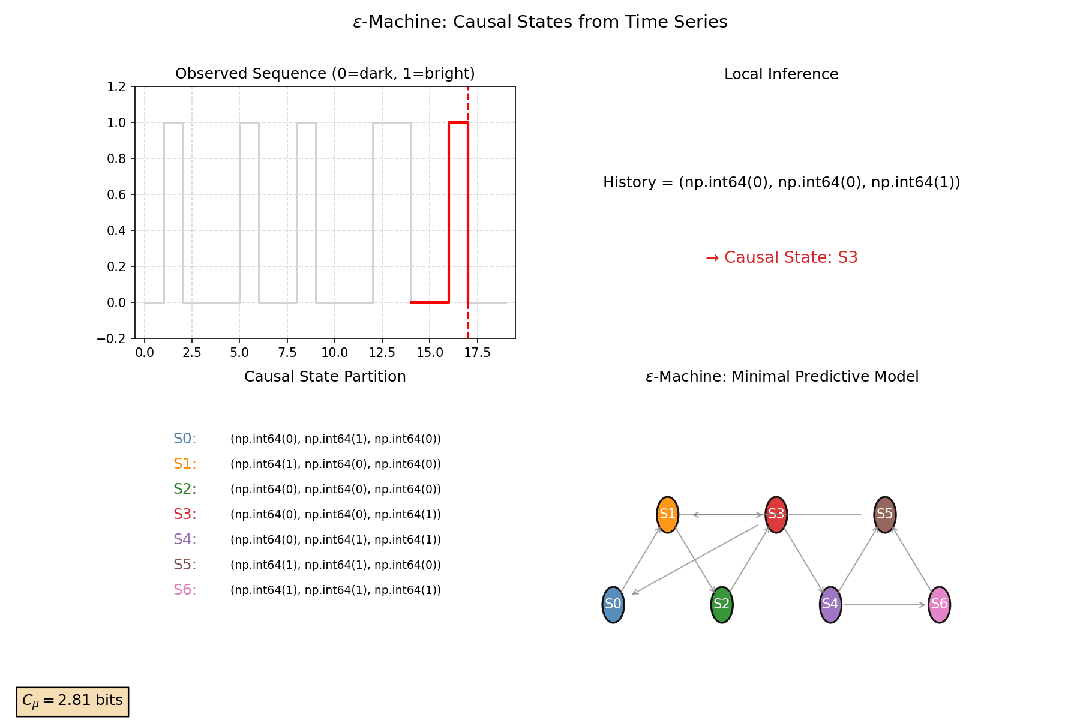
图7:因果态构建示意图
三、信息分解:解开信息的协同与冗余
传统的互信息 I(X;Y) 告诉我们X和Y共享了多少信息。但如果考虑第三个变量S(如一个环境刺激),问题就变得复杂了:X和Y所共享的关于S的信息,有多少是冗余的(都反映了S的相同信息)?有多少是协同的(只有当X和Y同时被观测时,才能获得关于S的独特信息)?
部分信息分解(PID) 旨在将I(S; X,Y) —— 由X和Y决定的关于目标S的总信息 —— 分解为四个部分:
- 冗余信息:由X和Y各自单独提供的、关于S的相同信息。
- X的特有信息:仅由X提供的关于S的信息。
- Y的特有信息:仅由Y提供的关于S的信息。
- 协同信息:只有当X和Y被同时考虑时,才能提供的关于S的信息。
I(X₁, X₂; Y) = Red(X₁, X₂ → Y) + Unq(X₁ → Y | X₂) + Unq(X₂ → Y | X₁) + Syn(X₁, X₂ → Y)
当源变量数量 N > 2 时,PID 会迅速复杂化。Williams & Beer 引入了冗余格——一个偏序集,用于枚举所有信息分配的可能“原子”。
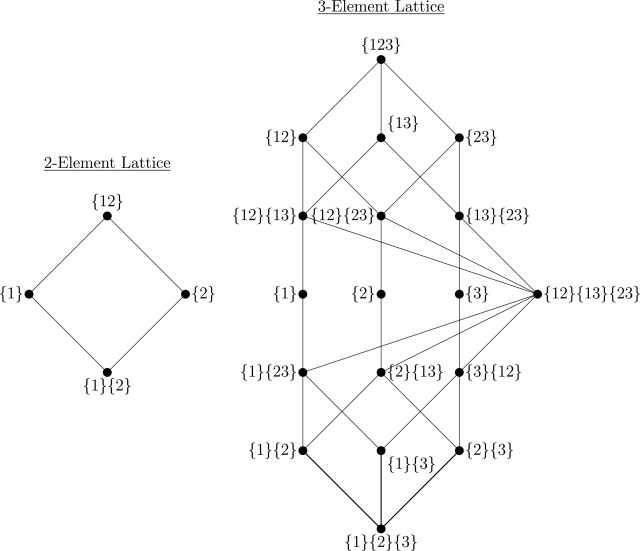
图8:两个源和三个源变量情况下的冗余晶格示例
在神经科学中,使用PID可以研究一组神经元是如何冗余地编码一个刺激以提高鲁棒性,又是如何协同地编码更复杂的特征。
PID也为从数据中推断网络结构提供了工具。通过计算所有可能变量对之间的互信息或传递熵,可以构建一个加权的、完全连通的图,再通过阈值化或统计检验推断显著连接。该方法能发现非线性相互作用,且对数据分布假设要求较低。
PED(部分熵分解) 是PID的自然推广。不同于PID分解互信息 I(X1,…,XN;Y) 时需要区分“源”与“目标”,PED直接分解联合熵 H(X1,…,XN),无需指定输入与输出。
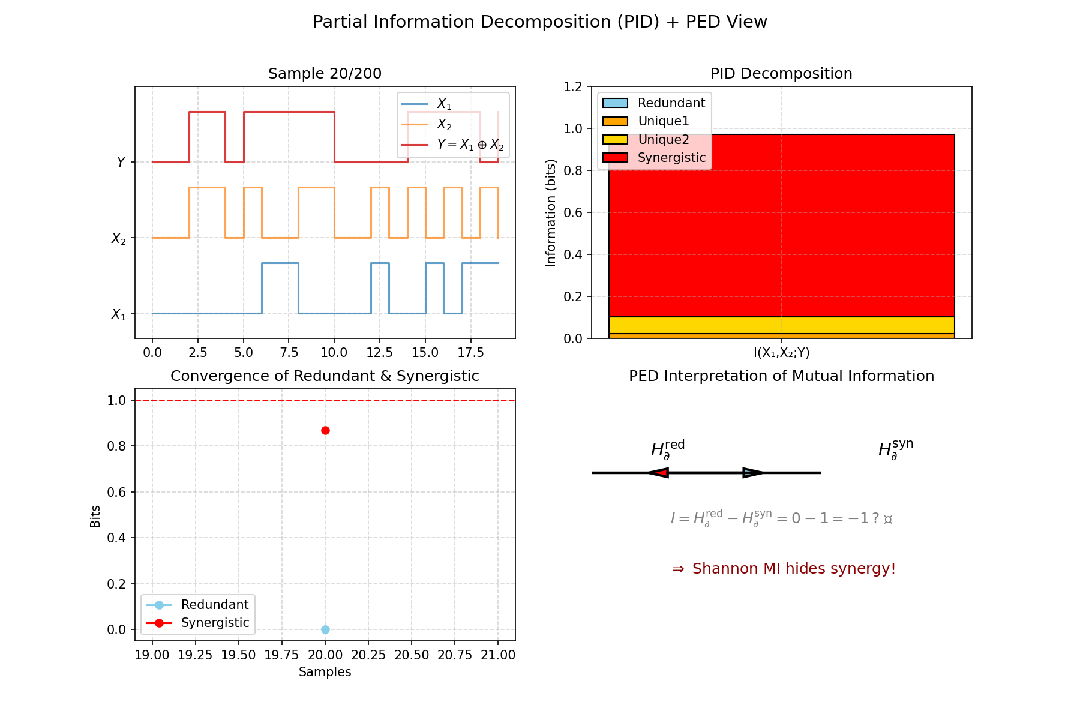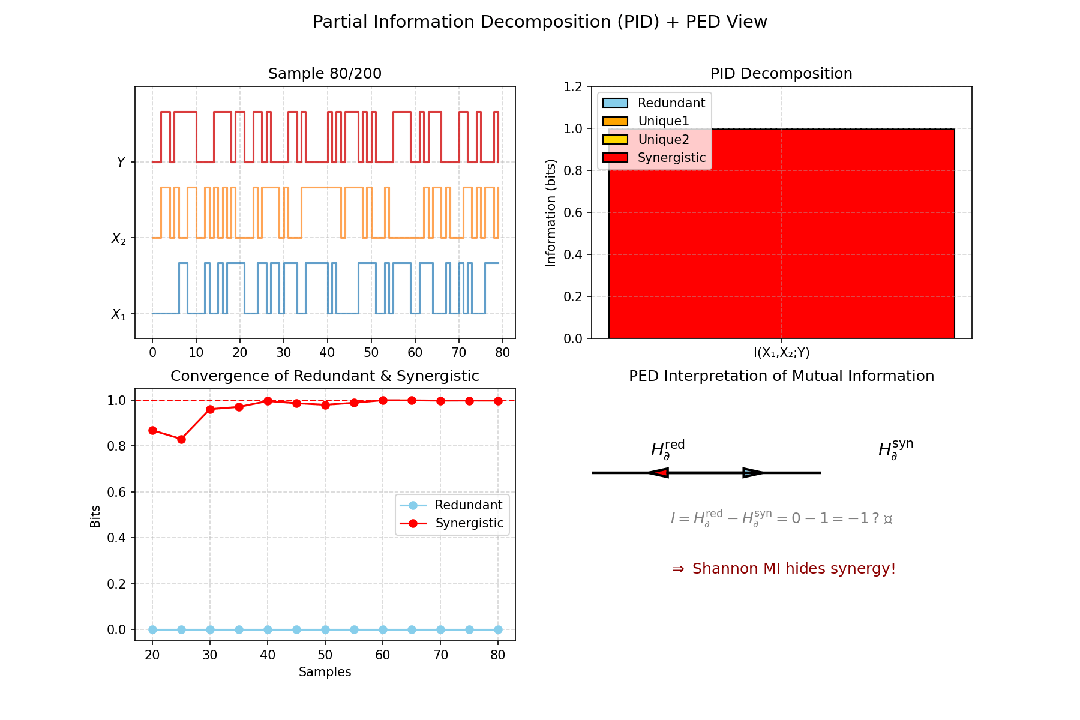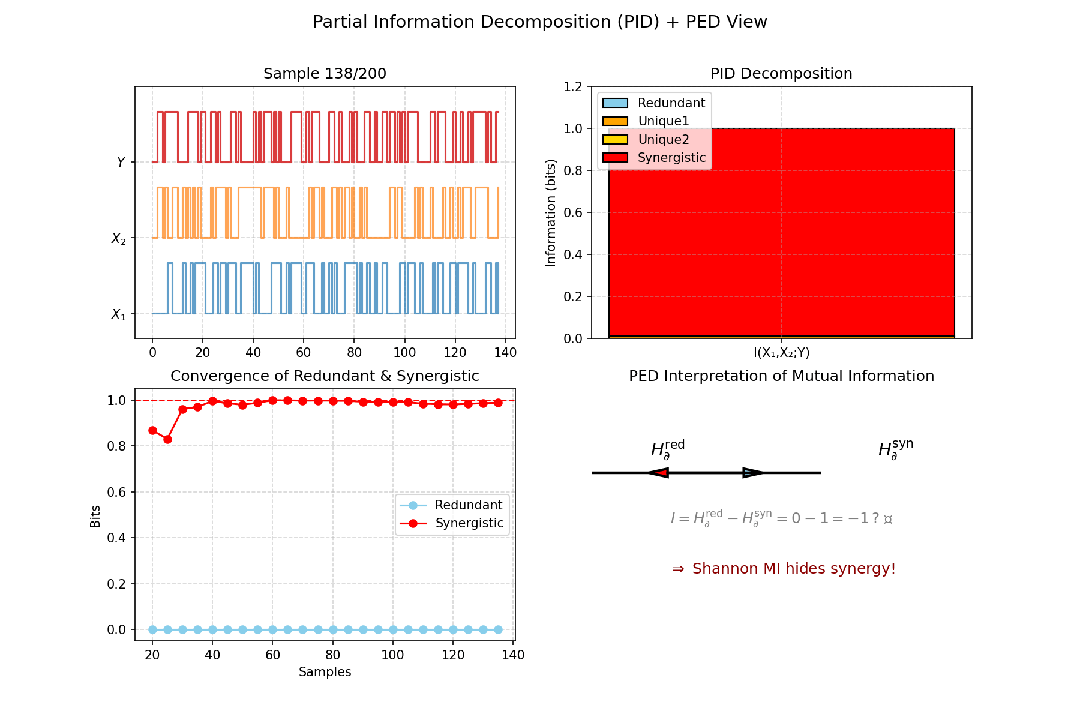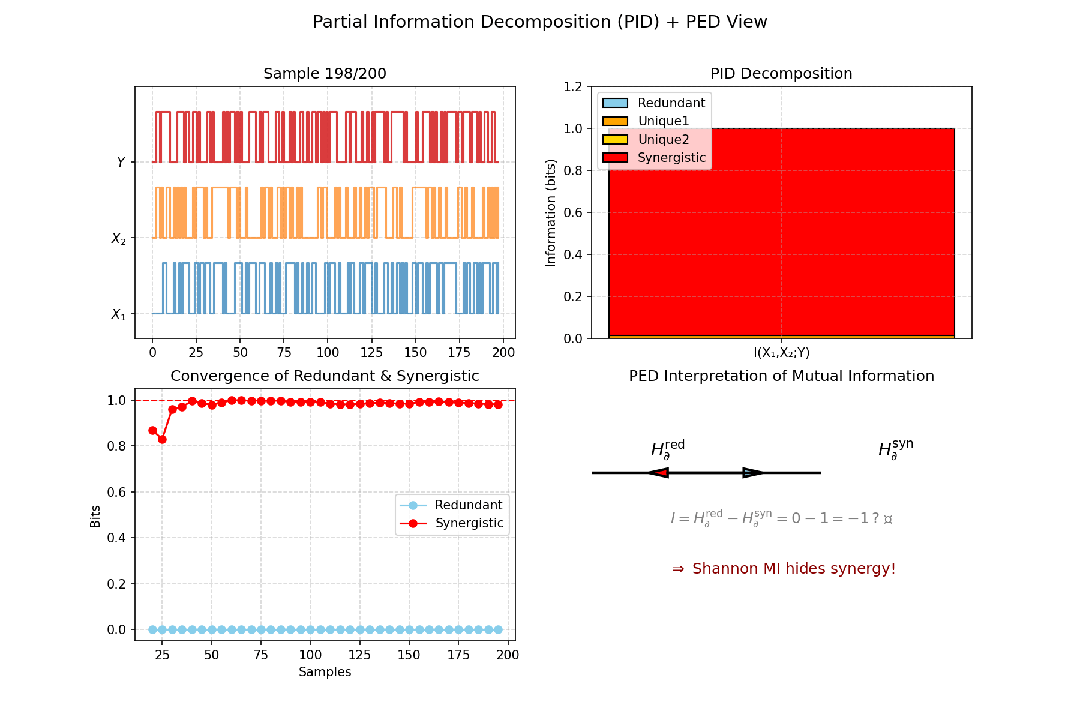
图9:以异或门(Y=X1⊕X2)为例,展示PID的累积收敛过程及PED视角
四、从成对关系到信息网络
网络是复杂系统建模的通用语言。信息论可以帮助我们从数据中构建两种主要的统计网络:
- 功能连接网络:由无向图构成,边权重为变量间的互信息,刻画瞬时协同变化。例如fMRI脑功能网络、基因共表达网络。
- 有效连接网络:由有向图构成,边权重为变量间的传递熵,刻画定向的因果或预测性影响。
当系统中存在高阶的协同或冗余效应时,基于成对关系的二元网络将无法描述。此时需要引入能连接多个节点的超边,从而构建超图或单纯复形来更准确地表征系统结构。
五、用信息论刻画复杂系统的整合与分离
复杂系统的核心特征在于其“整合”与“分离”的平衡。整合指系统所有元素相互作用的程度;分离指部分元素参与相对独立进程的程度。健康的大脑、成功的企业、全球政治都体现了这种平衡。
5.1 TSE-复杂性
Tononi, Sporns 与 Edelman 提出的 TSE-复杂性,通过遍历所有可能的子系统划分,检测每个“部分”与系统“剩余”部分之间的互信息分布。
- 全分离系统(如独立变量),TSE = 0。
- 全整合系统(如同步振子),TSE 也较低。
- 具有中等模块化结构的系统(模块内高整合、模块间弱连接),互信息随子系统大小非线性上升,TSE 达到峰值,表明系统处于信息处理能力最强的状态。
5.2 O-信息与S-信息
Rosas 等人提出的 O-信息(Ω) 与 S-信息(Σ) 进一步分解了复杂性的成分。
- Ω > 0:系统以冗余主导,信息有多个备份,稳健性高,适应性低。
- Ω < 0:系统以协同主导,信息仅存在于全局模式中,灵活性高,脆弱性高。
- Σ:反映总依赖密度,高 Σ 表示节点深度嵌入网络(如枢纽节点)。
5.3 整合信息度量 Φᵣ
Balduzzi和Tononi提出的 整合信息度量 Φᵣ,旨在捕捉系统“整体大于部分之和”的、基于动力学的、不可还原的信息结构。它量化了只有联合考虑所有部分的过去,才能最优预测整体未来的程度。
- 实验表明,蜂群决策时 Φᵣ 升高;癫痫发作(全脑病理性同步)时 Φᵣ 反而下降。
- Φᵣ 可作为系统是否具备“统一认知架构”的操作性检验指标,例如用于评估大型语言模型或机器人系统的信息整合程度。
对于多组件系统,可通过最小信息二分法遍历所有划分,寻找使 Φᵣ 最小的划分,该最小值反映了系统整体整合能力的下界。
六、使用信息论的实际困难与计算方法
在应用信息论时,最大的实践挑战之一是从有限的观测数据中准确估计概率分布及各种信息量。估计偏差不仅影响数值精度,更会系统性扭曲对高阶结构的推断。
主要挑战与方法:
- 离散数据的估计偏差:简单的“插件估计”会系统性地低估熵、高估互信息。常用校正方法包括 Miller–Madow 校正、置换检验构建零模型、贝叶斯估计器等。
- 连续数据的处理:
- 粗粒化(分箱):简单但信息损失严重,已不推荐。
- 参数法(如高斯估计器):仅能捕获线性依赖。
- 非参数法(如基于K近邻的KSG估计器):无需假设分布,能捕捉非线性依赖,是目前的主流方法,并可扩展至条件互信息、PID等。
- 计算工具:已有多个优秀的Python开源软件包可用于计算高阶信息度量,例如
dit 可用于部分信息分解(PID)。
此外,需注意信息论度量(如传递熵)指示的有向依赖不直接等同于因果关系,它依赖于数据背后的因果图假设。同时,要避免将“信息流”、“信息存储”等隐喻误解为物理实体。信息论本质上是关于不确定性推理的数学,它描述的是观察者如何减少对系统状态的不确定性。
七、未来方向与总结
在大数据时代,面对高维、混合类型的数据集,需要新的信息估计方法。神经信息估计器(如MINE, Mutual Information Neural Estimation)利用神经网络来估计信息度量,代表了一种在复杂系统科学中尚未被充分探索的新途径。
另一个前沿方向是利用信息度量(如 Φᵣ、O-信息)作为目标函数,来引导进化算法或优化人工系统(如机器人群体),旨在直接促使期望的复杂行为或计算属性的“涌现”。
总结来看,从香农熵到高阶的整合信息分解,信息理论为复杂系统研究提供了一套统一而强大的数学语言。它使我们能够量化系统哪部分在“记忆”,信息在何处是冗余或协同的,以及整体是否真的“大于部分之和”。通过这些工具,我们得以深入解析那些在多个尺度上、通过不确定性降低过程而展现出丰富结构和动力学的复杂系统。正如在机器学习中利用神经网络估计互信息(MINE方法)所展示的潜力,信息论与复杂系统的结合将继续为理解生命、认知和社会等核心奥秘提供关键的洞察力。