信息论熵与互信息：复杂系统动力学建模与网络重构的核心工具

无论是气候变化、流行病传播、金融市场波动，还是大脑的认知功能，这些系统都由大量组件构成，组件间存在多样且动态的互动。因为这些非平凡的互动具有如非线性、涌现、自适应和路径依赖等特征，导致其集体行为往往难以通过还原论预测。面对这些错综复杂的涌现现象，科学家们迫切需要一套强大而普适的数学语言来对其进行描述、量化和理解。

起源于通信领域的信息论，因其能够跨领域量化组件之间、系统与环境、整体与部分的互动，正逐渐成为复杂系统研究领域工具箱中不可或缺的一环。本文将基于 Thomas F. Varley 于 2025 年 12 月发表在《Physics Reports》上的一篇重要综述，系统阐述信息理论为何以及如何成为复杂系统科学的基石，并详解其核心概念、进阶工具与实际应用。

图：相关综述《Information theory for complex systems scientists: What, why and how》的封面

信息理论的基石：核心概念与直觉构建

文章首先详细讲解了信息理论的几个核心度量指标，最基础的概念无疑是熵。据说香农在提出信息论后，曾向冯·诺依曼请教应如何命名这种新的不确定性度量。冯·诺依曼回答：“你应该称之为熵，因为没人真正知道熵是什么，这样你在辩论中总是占上风。” 这个故事凸显了一个现实：尽管香农提及熵时最初的关注点或许狭隘，但他所构建的数学框架却异常通用，容易产生多种深刻的解读。

1.1 熵：不确定性的量化

想象一个天气预报。如果某地一年365天都是晴天，那么你对“明天天气”的不确定性为零，熵也为零。如果天气晴雨各半，你的不确定性最大，熵也最高。因此，熵衡量的是在得知具体结果之前，我们对一个随机变量取值的“惊讶”程度的期望值。

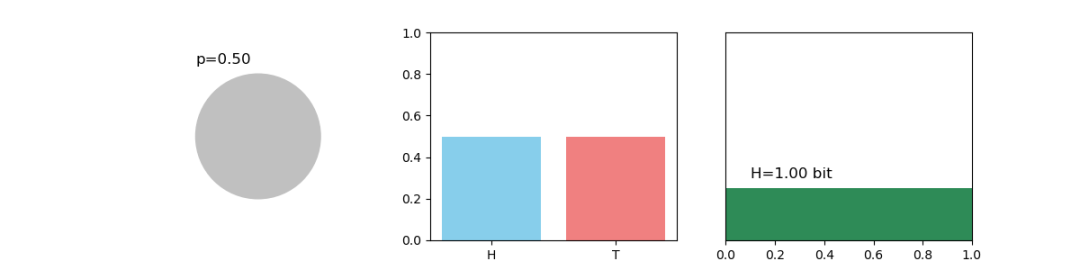
图1：信息熵示意图，不同概率分布对应的熵值不同

对于一个离散随机变量X，其香农熵H(X)的数学定义为 H(X) = -Σp(x)logp(x)。其中p(x)是X取值为x的概率。对数底数通常为2，此时熵的单位是比特。在神经科学中，一个神经元的放电序列的熵可以衡量其响应的可变性；在生态学中，物种分布模式的熵可以反映其空间分布的不确定性；在金融学中，一只股票价格的熵可以表征其波动性。

1.2 联合熵与条件熵

联合熵 H(X,Y) 衡量两个随机变量X和Y联合分布的不确定性。它总是大于等于单个变量的熵，但小于等于二者熵之和。条件熵 H(Y|X) 表示在已知随机变量X取值的情况下，对随机变量Y仍存在的不确定性。如果X和Y完全独立，则 H(Y|X) = H(Y)；如果Y完全由X决定，则 H(Y|X) = 0。

关系式 H(X,Y) = H(X) + H(Y|X) 直观地表明，X和Y的总不确定性，等于X自身的不确定性，加上已知X后Y剩余的不确定性。

1.3 互信息：依赖关系的纯粹度量

互信息 I(X;Y) 是信息理论的核心度量之一。它衡量通过观察一个变量，能获得关于另一个变量的平均信息量。或者说，它量化了X和Y之间的统计依赖性，其范围从0（完全独立）到 min(H(X), H(Y))（完全依赖）。

I(X;Y) = H(X) + H(Y) - H(X,Y)。变量X和Y之间的互信息等于它们各自不确定性的和，减去它们的联合不确定性。那部分被“抵消”掉的不确定性，正是由X和Y共享的信息。

相比只能捕捉线性关系的皮尔森相关系数，互信息能捕捉任何形式的统计依赖，包括非线性的、非单调的关系。例如，Y = X² 的关系，相关系数可能为0，但互信息值会很高。在脑网络中，可以用互信息来连接两个脑区，表示它们活动的同步性；在基因调控网络中，可以连接两个基因，表示其表达水平的协同变化。

图2：互信息在联合熵与条件熵关系中的拆解示意图

1.4 相对熵 （Kullback-Leibler散度）

相对熵衡量两个概率分布p和q之间的“差异”（严格来说不是距离，因为它不对称）。D_KL(p || q) 量化了当真实分布为p时，用分布q来近似所造成的信息损失。而互信息可以表示为 I(X;Y) = D_KL( p(x,y) || p(x)p(y) )。

从这个公式可以看出，互信息衡量的是X和Y的联合分布 p(x,y) 与它们假设独立时的分布 p(x)p(y) 之间的“差异”。差异越大，说明它们越不独立，共享信息越多。例如，考虑投掷一个正常骰子和一个有偏骰子这两个独立事件，投掷五次过程中相对熵的动态变化如下图所示。

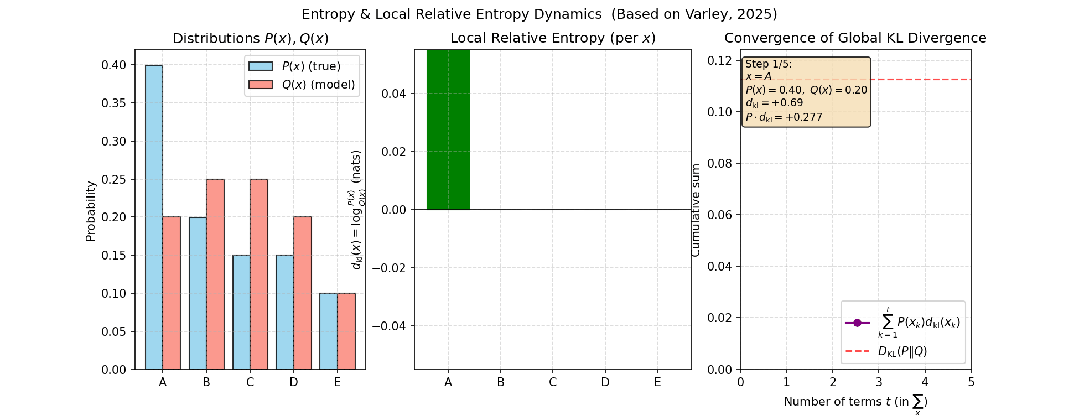
图3：使用两个不同分布（正常 vs. 有偏）骰子时，相对熵随抽样次数增加而收敛的过程

基础的信息度量（如互信息）如同给我们一张复杂系统的静态快照，我们能看出哪些节点之间有连接，但无法知晓信息是如何在这些连接中流动的，也无法理解这些连接背后的深层结构。接下来要介绍的指标，会将这张静态照片升级为一部动态的、可解构的影片。

信息论如何直接描摹复杂系统的动态特征

复杂系统中，信息的传递是动态的、随时间演化的。信息动力学旨在量化信息在系统内部及与环境之间的产生、存储、传递和修改。

2.1 传递熵

传递熵由Thomas Schreiber提出，是互信息在时间序列上的推广。它衡量的是，在已知Y自身过去历史的情况下，X的过去历史能为预测Y的当前状态提供多少额外信息，即定向信息流。例如，在神经科学中，传递熵可用于判断是脑区A的活动影响了脑区B，还是反之，从而推断出因果关系的方向，这比仅进行非方向性因果量化的格兰杰因果检验更强。

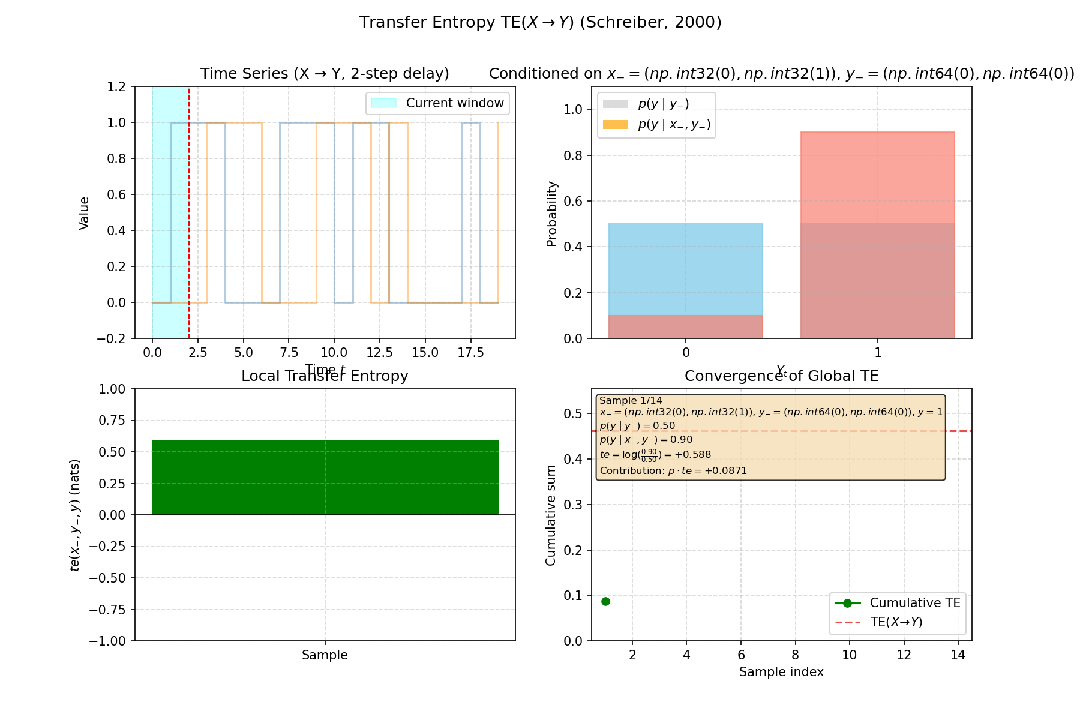
图4：在一个简单构造的因果系统（Y受X的两步延迟影响）中，X到Y的转移熵为正，揭示了定向的信息流

2.2 主动信息存储

主动信息存储（AIS）衡量一个系统组成部分的过去历史中，有多少信息与其当前状态相关。这量化了系统内部记忆或信息存储的能力。一个具有高主动信息存储的单元，其行为在很大程度上由其自身的历史决定。

应用AIS分析混沌时间序列：虽然混沌系统是确定性的，但由于其对初始条件的极端敏感性（蝴蝶效应），其短期历史对预测当前状态非常有价值，但长期历史的预测价值会迅速衰减。因此，当我们设定一个适当的过去窗口长度（例如，10个时间步）时，计算出的AIS会是一个中等偏高的值。这表明系统在短期内是有“记忆”的。

在金融市场中，常见的有效市场假说认为，股价的历史信息不能预测未来收益，即收益率序列接近随机游走。此时计算出的AIS值会非常低，接近零。这意味着资产的过去价格对其当前价格几乎没有提供额外的信息，支持了“市场无记忆”的观点。反之，如果发现某只股票的AIS值持续较高，则可能意味着存在可预测的模式，违背了有效市场假说。

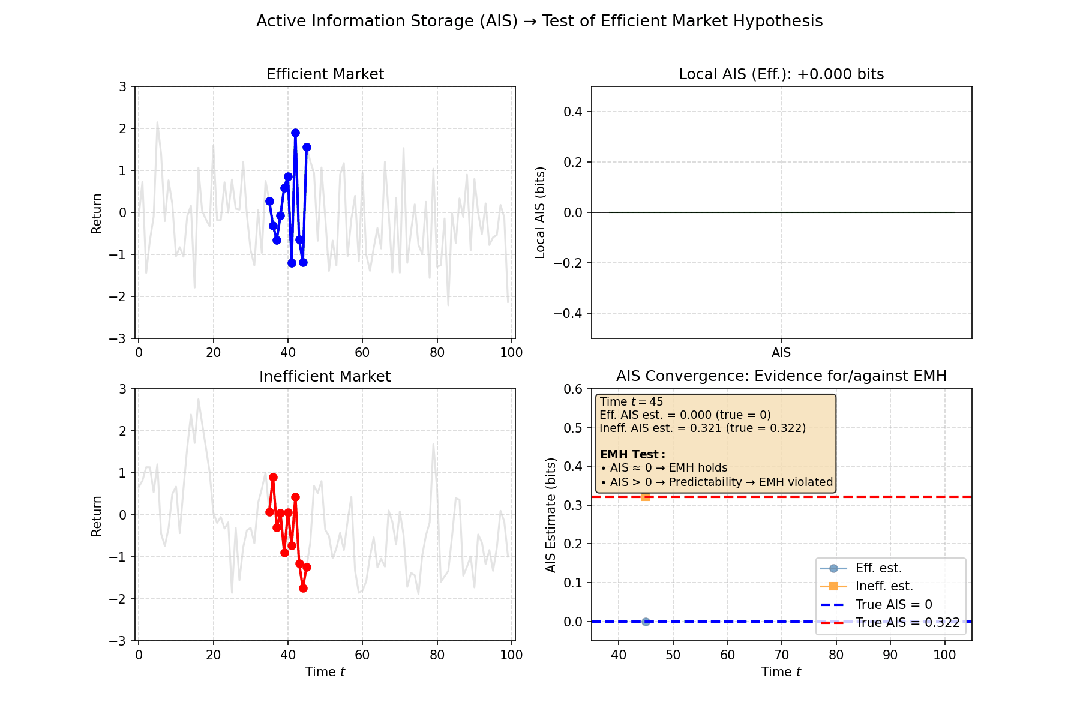
图5：满足与违背有效市场假说的模拟场景下，对应的主动信息存储（AIS）值不同

2.3 整合信息论与因果态

整合信息论由神经科学家Giulio Tononi提出，试图度量意识。其核心思想是，一个系统是否具有“意识”或其程度，取决于其各个部分整合信息的程度，即整个系统所产生的信息大于其各部分信息之和的程度。考虑一个由百万个光电管组成的高分辨率数码相机。每个像素都能高保真地记录光信息，整个传感器接收的信息量巨大。但是，如果你将传感器切割成两半，每一半仍然能很好地工作。传感器各部分之间几乎没有因果相互作用（一个像素的状态不影响相邻像素）。因此，这个系统的整合信息Φ非常低，故而照相机不可能有意识体验。

而大脑的不同区域以极其复杂的方式相互作用。视觉皮层接收的信息需要与记忆、情感、语言等区域进行整合，才能形成“看到一朵红玫瑰”这样统一、不可分割的体验。如果因为疾病导致大脑不同区域的联系减弱（如裂脑症），这种统一的体验就消失了。因此，大脑作为一个整体的信息远超其部分信息之和，其整合信息Φ被认为非常高。整合信息论由此将Φ与意识的程度直接联系起来。然而，Φ的计算在实践上对于像大脑这样的复杂系统极其困难，因此该理论在学界存在巨大争议。

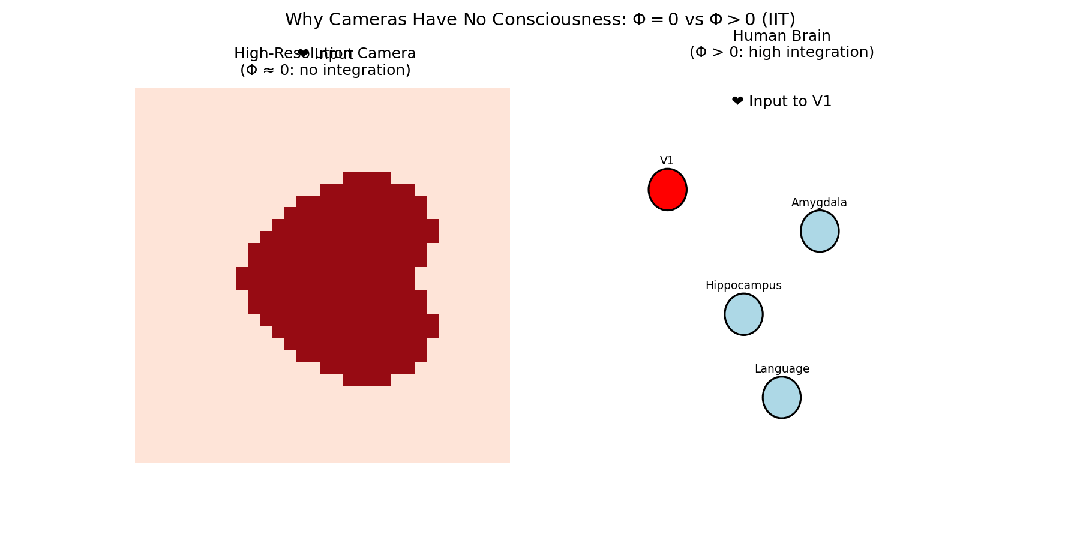
图6：对比高分辨率相机与人类大脑在视觉信息处理上的整合程度（Φ值）差异

2.4 统计复杂性与ϵ-机器

通过分析时间序列的历史数据，可以将能预测相同未来状态的所有历史归入同一个“因果态”。这是一种对系统动态过程的最优压缩表示。统计复杂性是这些因果态分布的熵。统计复杂性衡量了为准确预测未来，系统必须记住多少关于过去的信息。

该指标衡量的是系统为了生成观测到的时间序列，所需要记住的关于其过去的最小信息量。一个具有中等统计复杂性的系统，通常具有丰富的内部结构和动态模式。

想象你观测一只萤火虫的闪光序列：亮、暗、亮、亮、暗……初看随机，但若某些“历史模式”（如“亮-暗”）总是预测下一刻“亮”，而另一些（如“暗-暗”）总导向“暗”，那么这些历史就应被归为两类——它们虽细节不同，却对未来有相同的预测效力。

这些具有预测效力的历史，可视为因果态：即所有能生成相同未来条件分布的历史，被等价归并为一个状态节点。而由这些因果态构成的最小、最简、最优预测器被称为ϵ-机器。无论是统计复杂性的最优压缩，还是ϵ-机器的内在状态结构的不可约性，这两个概念都说明了复杂系统之所以复杂，在于其内在状态结构的不可约性。

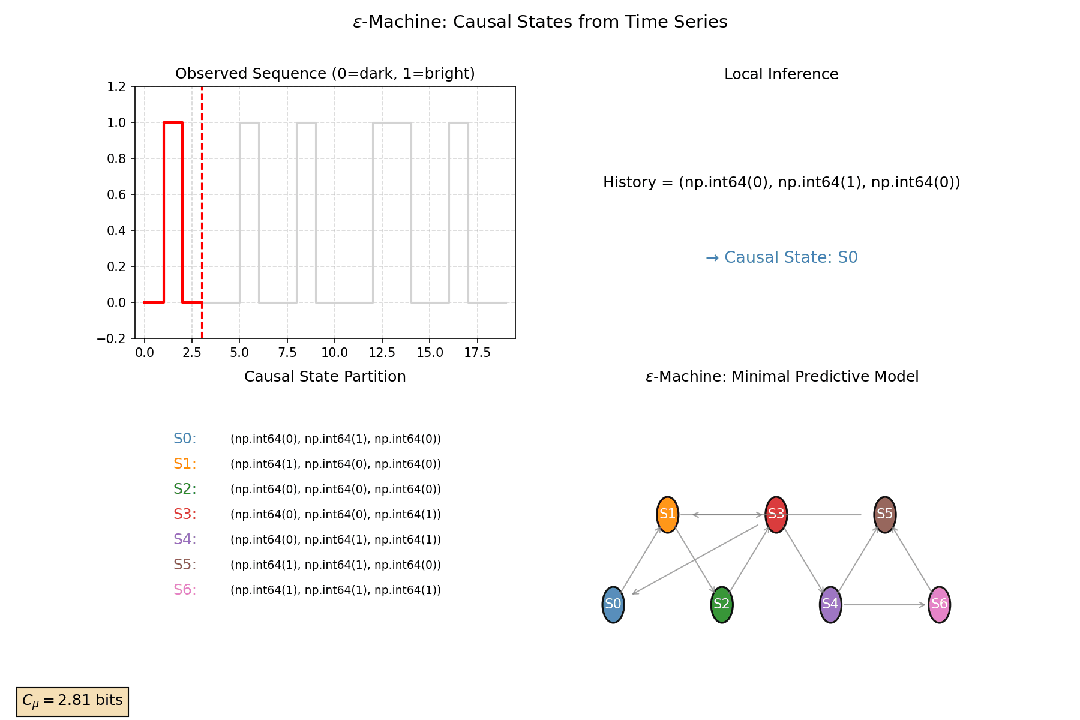
图7：从一段二元时间序列中构建ϵ-机器并识别因果状态的过程示意图

信息分解：解开信息的协同与冗余

传统互信息 I(X;Y) 告诉了我们X和Y共享了多少信息。但如果考虑第三个变量S（例如，一个环境刺激或一个共同驱动因素），问题就变得复杂了：X和Y所共享的信息，有多少是冗余的（例如，都反映了S的信息）？有多少是协同的（例如，只有当X和Y同时被观测时，才能获得关于S的独特信息）？

3.1 部分信息分解

部分信息分解旨在将 I(S; X,Y)（由X和Y共同决定的关于目标S的总信息）分解为四个部分：

1. 冗余信息：由X和Y各自单独提供的、关于S的相同信息。
2. X的特有信息：仅由X提供的关于S的信息。
3. Y的特有信息：仅由Y提供的关于S的信息。
4. 协同信息：只有当X和Y被同时考虑时，才能提供的关于S的信息。

数学上可表示为：I(X1,X2;Y) = Red + Unq(X1) + Unq(X2) + Syn。

当源变量数量 N > 2 时，部分信息分解迅速复杂化。Williams & Beer 引入了冗余格的概念——一个偏序集，用于枚举所有信息分配的可能“原子”。

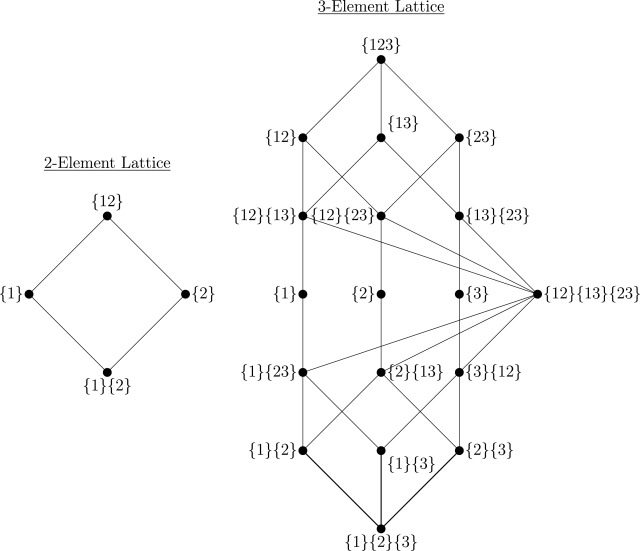
图8：两个源变量和三个源变量情况下的冗余晶格结构示例

在神经科学中，使用PID可以研究一组神经元是如何冗余地编码一个刺激以提高鲁棒性，又是如何协同地编码更复杂的特征。这有助于理解神经群体编码的原理。

3.2 从PID到PED

PED 是 PID 的自然推广。不同于 PID 对互信息 I(X1,…,XN;Y) 的分解（需指定“来源”与“目标”），PED 直接分解联合熵 H(X1,…,XN)，无需区分输入与输出，提供了一个更对称的视角来审视多元变量系统中的信息结构。

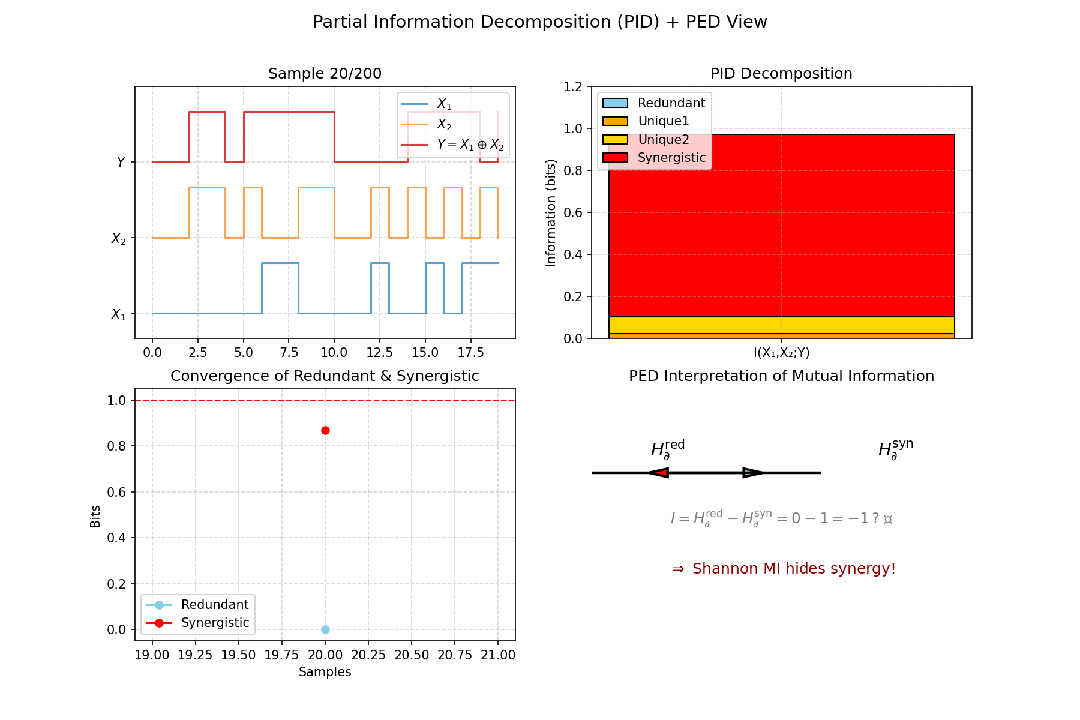
图9：以异或（XOR）关系为例，展示部分信息分解（PID）的收敛过程及对应的PED视图

从成对关系到高阶信息网络

网络是复杂系统建模的通用语言。网络可按构建方法分为两类：第一类是物理网络（如航空网、白质纤维束），其中边对应真实物理连接，结构可直接观测；另一类是统计网络，其中的边对应统计依赖性，需从数据推断，可使用信息论中的互信息等度量来刻画。

统计网络又可按是否包含方向，分为两类：

• 功能连接网络：由无向图构成，边权重为变量间的互信息，刻画瞬时共变，例如fMRI脑功能网络、基因共表达网络。
• 有效连接网络：由有向图构成，边权重为变量之间的转移熵，刻画事件X对事件Y在排除Y自身记忆下，对预测Y的增量预测能力。

当系统中存在显著的协同或冗余效应时，常规的基于成对相互关系构建的二元网络将无法充分描述。此时需引入能包含三元或更高阶相互作用的表示方法，如带有超边的超图或单纯复形。

用信息论刻画复杂系统的整合与分离

复杂系统的核心特征之一在于其“整合”与“分离”的平衡。整合指的是系统所有元素相互作用并相互影响的动态过程，而分离则指的是系统部分元素参与自身进程，且这些进程不与其他元素共享的动力学特征。

以大脑为例：特定脑区参与某些过程而不参与其他过程（功能分离），然而同时，大脑整合程度足够高，以至于所有不同的局部过程可以整合为一个统一的、具有单一意识的整体。有研究假设这种整合与分离的平衡对于健康的大脑功能至关重要。

类似地，在经济领域，成功的公司维持着健康的分离（各分支部门各司其职），同时所有工作都由中央执行办公室进行监督和整合。这种整合与分离的混合本质上是一种多尺度现象。

4.1 TSE复杂性与O-信息

1994年，Tononi, Sporns 与 Edelman 提出 TSE-复杂性，通过遍历所有可能的子系统划分，检测“部分”与“剩余”之间的互信息分布。具有中等模块化特征的系统（模块内高整合、模块间弱连接），其TSE复杂性达到峰值，表明系统处于信息处理能力较强的状态。由于TSE的计算需枚举所有子集，对大规模系统几乎不可行。

TSE 告诉我们“有多复杂”，却未揭示“复杂在何处”。Rosas 等人提出的 O-信息 与 S-信息 则进一步分解复杂性的成分。Ω > 0，则系统以冗余主导，对应稳健性高；Ω < 0，则系统以协同主导，对应灵活性高、脆弱性高；S信息Σ则反映总依赖密度，高 Σ 表示节点深度嵌入网络。

4.2 集成信息度量 Φᵣ

Balduzzi和Tononi提出的集成信息度量（如 Φᵣ）旨在捕捉系统“整体大于部分之和”的不可还原性信息结构。它将过去作为一个整体，考察对未来产生不可分解的预测力。若该值大于零，说明只有联合考虑所有部分的过去，才能最优预测整体未来，存在不可约的跨变量协同演化。

Φᵣ 通过从整合信息分解中剔除纯冗余项，用以衡量系统是否真正作为一个统一体进行计算。实验证明蜂群决策时 Φᵣ 升高；癫痫发作（全脑同步）时 Φᵣ 反而下降。由于Φᵣ是系统“因果不可还原性”的量化指标，可作为人工系统（如LLM、机器人）是否具备“统一认知架构”的一种可操作检验。

对于包含多个组件的系统，常通过最小信息分割来寻找系统最脆弱的整合环节，其计算出的Φᵣ值是整体整合能力的下界。

使用信息论的实际困难

在论述了信息论在复杂系统中的种种应用后，文章也指出了实际应用时面临的挑战：需要从有限的观测数据中估计概率分布与信息量。估计偏差不仅影响数值精度，更会系统性扭曲高阶结构推断。

• 离散数据：简单的“插件估计”会导致熵被低估、互信息被高估，需使用 Miller–Madow 校正、置换检验或贝叶斯估计器等方法。
• 连续数据：方法更复杂。粗粒化（分箱）简单但信息损失严重；参数法（如高斯估计器）仅捕获线性依赖；目前主流推荐使用非参数密度法，如基于 k-近邻的 Kozachenko–Leonenko（熵估计）和 Kraskov–Stögbauer–Grassberger（互信息估计）方法，它们无需假设分布且可扩展至条件互信息、PID等。

此外，信息论应用还面临其他局限：

1. 因果推断：信息论度量的有向指标（如传递熵）是因果关系的必要条件而非充分条件，不代表绝对的因果关系，仍依赖先验知识或因果假设。
2. 解释隐喻：语言上的“信息流”、“存储”等隐喻易被误读为物理实体，而信息论本质上是关于不确定性中推理的数学，它描述的是我们如何减少对世界的认知不确定性。
3. 观察者依赖性：信息总是相对于观察者的模型，不存在绝对的“系统自身的信息”。

未来方向与总结

在大数据时代，面对数千个特征和数千万样本的数据集，需要新方法来学习元素组之间的复杂信息依赖关系。神经信息估计器（如 MINE - Mutual Information Neural Estimation）使用神经网络来估计信息论指标，代表了一种在复杂性科学中尚未得到充分探索的新途径。

此外，用 Φᵣ、O-信息等度量作为目标函数，引导进化算法或人工生命系统的设计，使其涌现出期望的复杂行为，也是未来富有前景的研究方向。

总结来看，从香农熵到整合信息分解，信息理论提供了一套统一的数学语言，用以刻画从预测、整合到涌现的多尺度过程。通过信息论，我们能够知道系统的哪部分在记忆，哪些信息是共享的、独有的、还是协同涌现的，整体是否真的大于部分之和。这些度量是理解复杂系统结构和动态的自然工具，这些系统可能富含高阶冗余、协同作用和计算过程，这些特征的外在表现为不同尺度上的不确定性降低。

文章题目：Information theory for complex systems scientists: What, why, and how
文章链接：https://www.sciencedirect.com/science/article/pii/S037015732500256X
发表时间：2025年12月8日
文章来源：Physics Reports