GMM高斯混合聚类详解：从Python原理到scikit-learn实践，突破K-Means局限

本文深入探讨高斯混合模型，一种能够克服K-Means局限性的强大聚类算法。GMM不仅能够处理复杂的数据分布，还提供了概率性的聚类结果。我们将通过对比K-Means，展示GMM在非球形数据上的优势，并介绍其作为密度估计工具的应用，包括如何选择最优的组件数目。

一、GMM：K-Means的进化

K-Means聚类模型简单易懂，但其非概率的本质以及简单的“距离簇中心最近”的归类方式，导致其在处理许多复杂现实数据时效果不佳。高斯混合模型可以看作是K-Means的拓展，它有效克服了这些缺点。

二、GMM的动机：K-Means的不足

首先，我们回顾K-Means的局限性，并以此引出GMM的优势。K-Means对于分离度良好的数据聚类效果出色。如下例所示，其分类结果与肉眼观察非常接近：

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1] # 翻转坐标轴使图表更直观

kmeans = KMeans(4, random_state=0)
labels = kmeans.fit_predict(X)
plt.scatter(X[:,0], X[:, 1], c=labels, alpha=0.7)
plt.show()

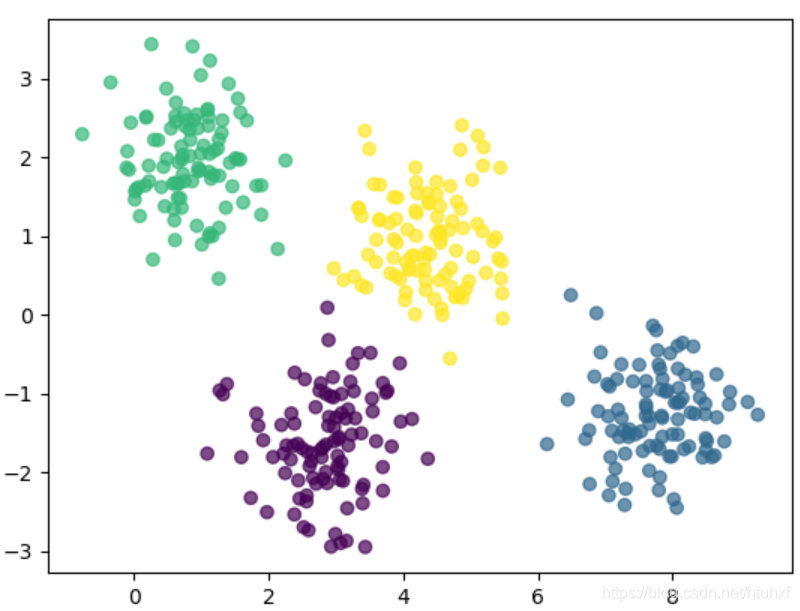
可以看到，大部分数据点都被正确归类。然而，位于簇边界附近的点，归到任何一个簇似乎都说得通，而K-Means无法给出每个点属于各个簇的概率值。

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt

def plot_kmeans(kmeans, X, n_cluster=4, rseed=0, ax=None):
    labels = kmeans.fit_predict(X)
    ax = ax or plt.gca()
    ax.axis('equal')
    ax.scatter(X[:, 0], X[:, 1],
               c=labels, alpha=0.7, ec='black', lw=1,
               s=40, zorder=2)
    centers = kmeans.cluster_centers_
    rads = [cdist(X[labels==i], [centers[i]]).max() for i in range(len(centers))]
    for center, rad in zip(centers, rads):
        ax.add_patch(plt.Circle(center, rad,
                                fc='grey', ec='black',
                                lw=3, alpha=0.5, zorder=1))

X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1]
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X)
plt.show()

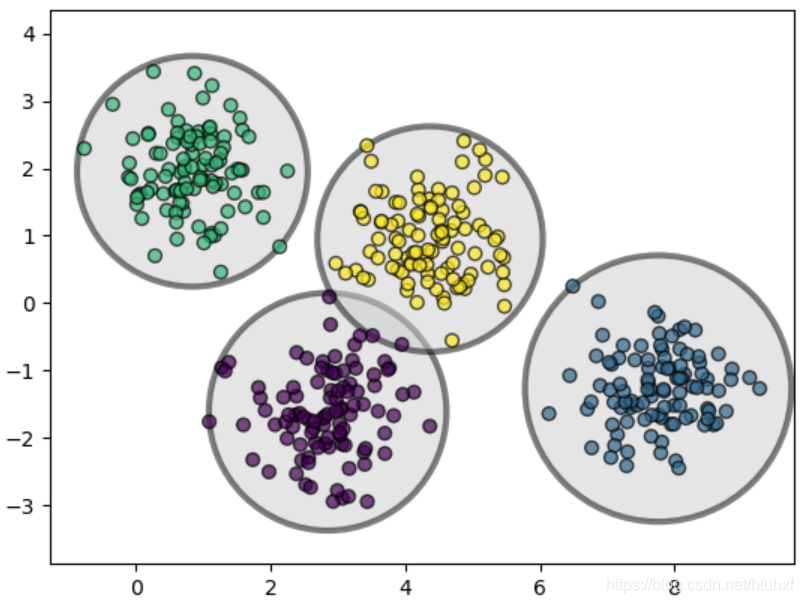
上图清晰地展示了K-Means本质上是基于圆形边界进行聚类的，因此最适合呈现球形分布的数据。对于拉长的椭圆形、矩形等其他形状的数据分布，其效果就不理想了。

import numpy as np
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))

kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)
plt.show()

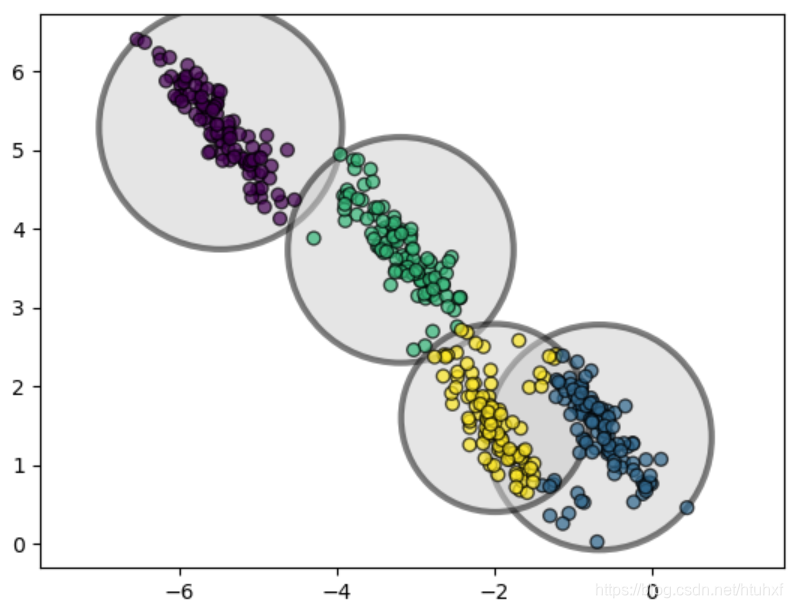
上图中，非球形分布的数据点未能被很好地区分。

总结K-Means的两大缺点：一是适用的数据分布形状有限；二是无法提供聚类归属的概率信息。很自然地，我们会想：如果聚类的边界可以是椭圆而非仅限于圆形，并且算法能综合考虑数据点到所有簇中心的“距离”（相似度）而不仅仅是最近的簇中心，那该多好。这正是高斯混合模型所提供的。

三、从K-Means到高斯混合模型

高斯混合模型假设数据是由多个高斯分布混合生成。在简单情况下，它的表现与K-Means相似。

from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

X, y_ture = make_blobs(n_samples=400, centers=4,
                        cluster_std=0.6, random_state=0)
X = X[:, ::-1]

gm = GaussianMixture(n_components=4)
labels = gm.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, alpha=0.7)
plt.show()

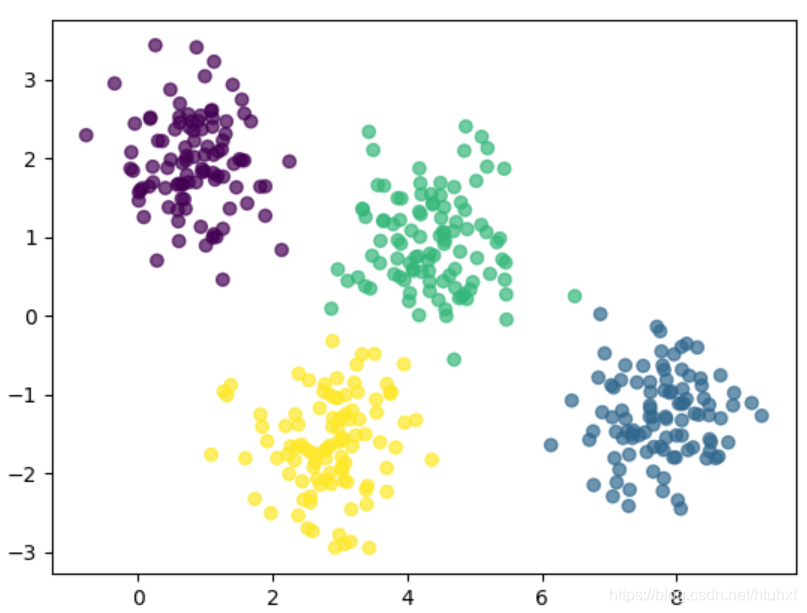
此外，GMM模型能够计算每个样本点属于各个簇的概率，通过predict_proba方法实现。

probs = gm.predict_proba(X)
print(probs[:5])
# 输出示例
# [[1.75162717e-22 4.69238090e-01 2.76240973e-07 5.30761633e-01]
#  [4.71110558e-15 1.97106146e-17 9.99999999e-01 9.22826700e-10]
#  ... ]

我们可以将概率大小可视化，点的大小反映其最大归属概率。

size = 50 * probs.max(1) # 修正：取每个样本的最大概率
plt.scatter(X[:, 0], X[:, 1], s=size, c=labels, alpha=0.7)
plt.show()

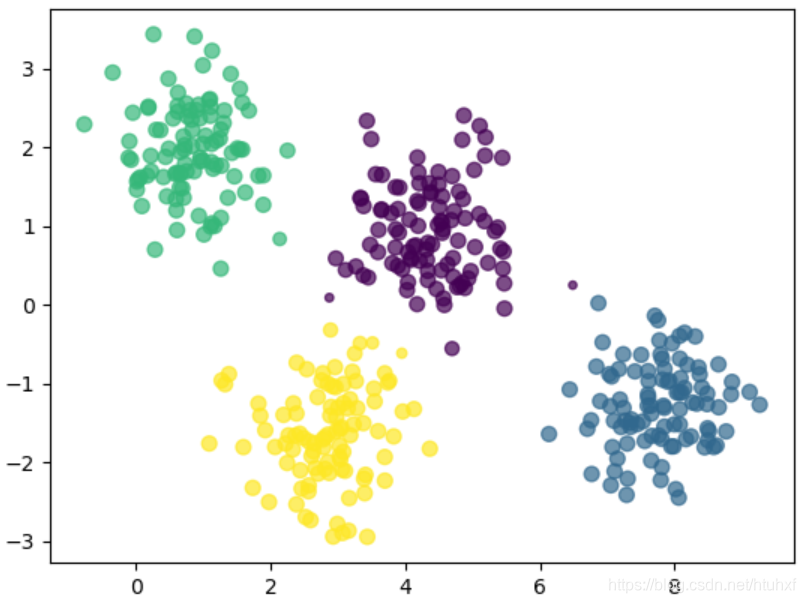
GMM采用期望最大化算法进行迭代优化，其步骤与K-Means相似：

1. 初始化各个高斯分量的参数（均值、协方差、权重）。
2. 重复以下步骤直至收敛：
   • E步（期望）：针对每个数据点，计算其属于各高斯分量的后验概率（即“责任”）。
   • M步（最大化）：利用E步计算出的“责任”值，更新每个高斯分量的参数（均值、协方差、权重）。

与K-Means相比，GMM最大的特点是其生成的簇具有椭圆形的概率边界。

from matplotlib.patches import Ellipse
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import numpy as np

def draw_ellipse(position, covariance, ax=None, **kwargs):
    ax = ax or plt.gca()
    if covariance.shape == (2, 2):
        U, s, Vt = np.linalg.svd(covariance)
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
        width, height = 2 * np.sqrt(s)
    else:
        angle = 0
        width = height = 2 * np.sqrt(covariance)
    for n in range(1, 4):
        ax.add_patch(Ellipse(position, n*width, n*height, angle, **kwargs))

def plot_gm(gm, X, label=True):
    labels = gm.fit_predict(X)
    if label:
        plt.scatter(X[:, 0], X[:, 1], c=labels, alpha=0.7, zorder=2, ec='black')
    else:
        plt.scatter(X[:, 0], X[:, 1], alpha=0.7, zorder=2, ec='black')
    plt.axis('equal')
    w_factor = 0.2 / gm.weights_.max()
    for pos, covar, w in zip(gm.means_, gm.covariances_, gm.weights_):
        draw_ellipse(pos, covar, alpha=w * w_factor)

X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.6, random_state=0)
X = X[:, ::-1]
gm = GaussianMixture(n_components=4, random_state=42)
plot_gm(gm, X)
plt.show()

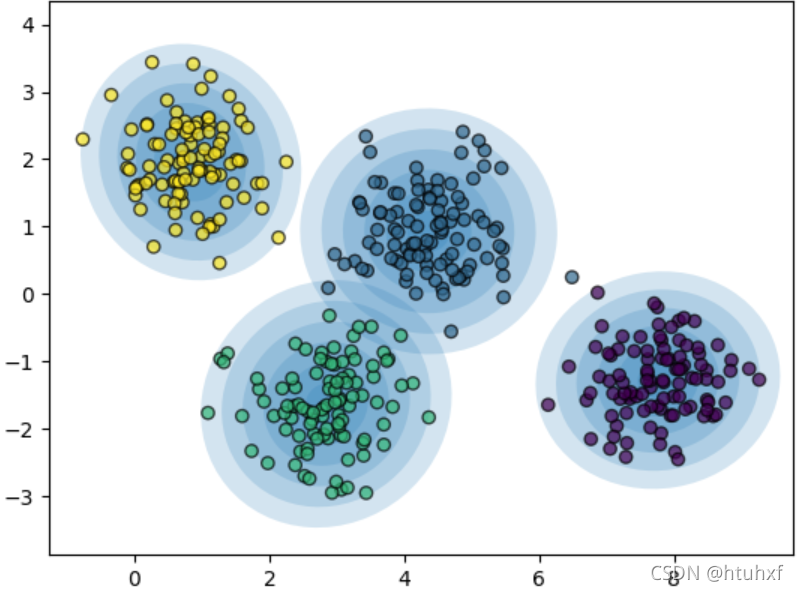
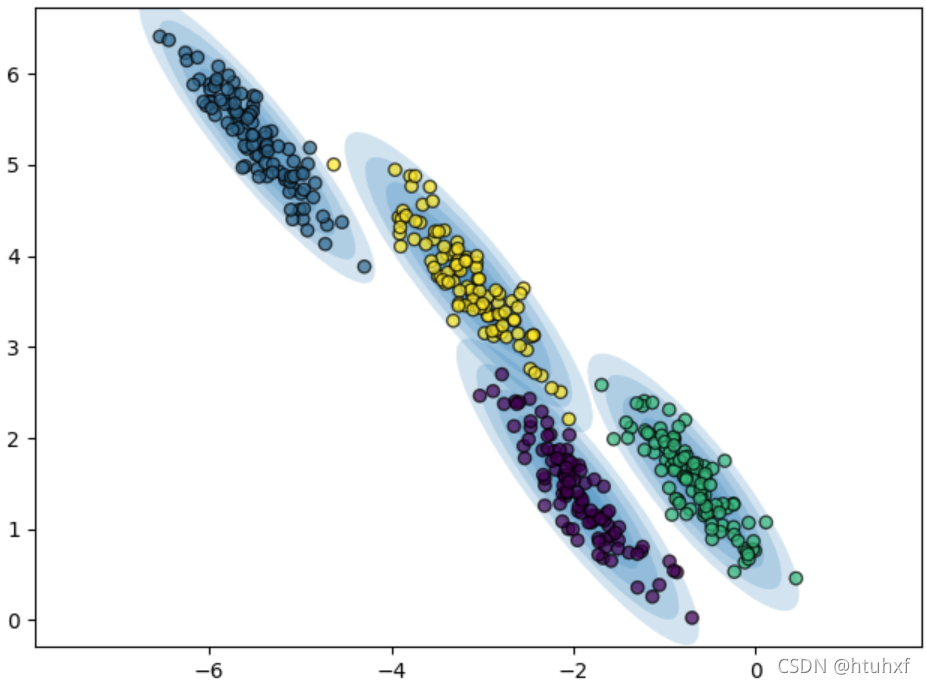
现在，用GMM来处理之前K-Means效果不佳的拉长数据，可以看到效果提升显著。

rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
gm = GaussianMixture(n_components=4, random_state=0)
plot_gm(gm, X_stretched)
plt.show()

附注：协方差类型的选择

在sklearn.mixture.GaussianMixture中，covariance_type参数有四个选项：{‘full’ (默认), ‘tied’, ‘diag’, ‘spherical’}，它们控制着每个高斯分量协方差矩阵的自由度，从而决定了椭圆簇的形状。

• spherical：每个簇的协方差矩阵是一个标量乘以单位矩阵。意味着簇是圆形的，所有方向方差相同。这是最简单的形式，计算最快。
• diag：每个簇的协方差矩阵是对角矩阵。意味着椭圆的轴向与坐标轴平行，但长短轴可自由变化。
• tied：所有簇共享同一个协方差矩阵。意味着所有簇的形状、大小和方向都相同。
• full：每个簇都有自己独立的全协方差矩阵。意味着每个簇的椭圆方向、大小都可以自由独立变化，最为灵活，但参数也最多。

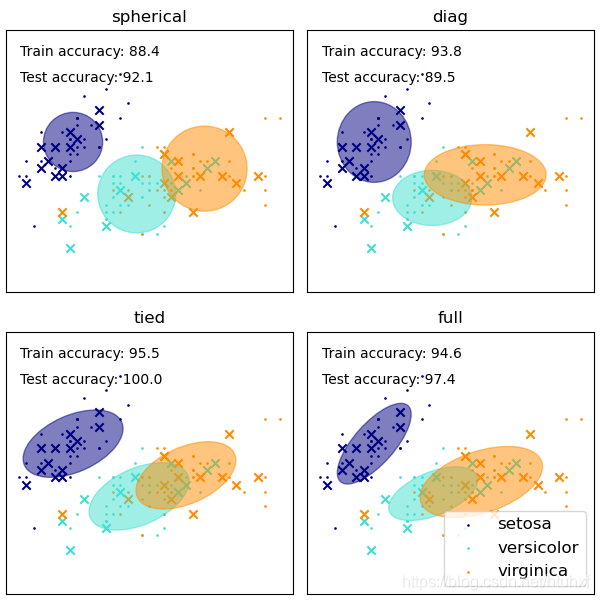
理解这些协方差类型有助于在特定场景下权衡模型复杂度和拟合效果。

四、作为密度估计的GMM

虽然GMM常用于聚类，但其本质是一个密度估计模型。这意味着其首要目标是建模数据的概率分布，而非单纯给数据点打标签。例如，我们考虑一个“双月牙”形状的数据集。

from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
Xmoon, ymoon = make_moons(250, noise=0.05, random_state=0)
plt.scatter(Xmoon[:, 0], Xmoon[:, 1], alpha=0.8, ec='black')
plt.show()

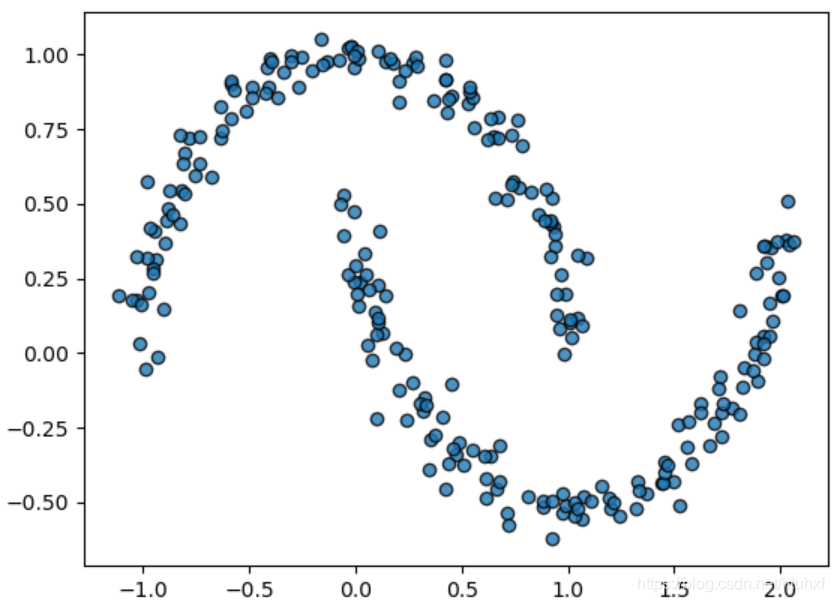
如果我们强行设定n_components=2进行聚类，结果并不符合直觉上的“月牙”划分。

gm = GaussianMixture(n_components=2, random_state=0)
plot_gm(gm, Xmoon)
plt.show()

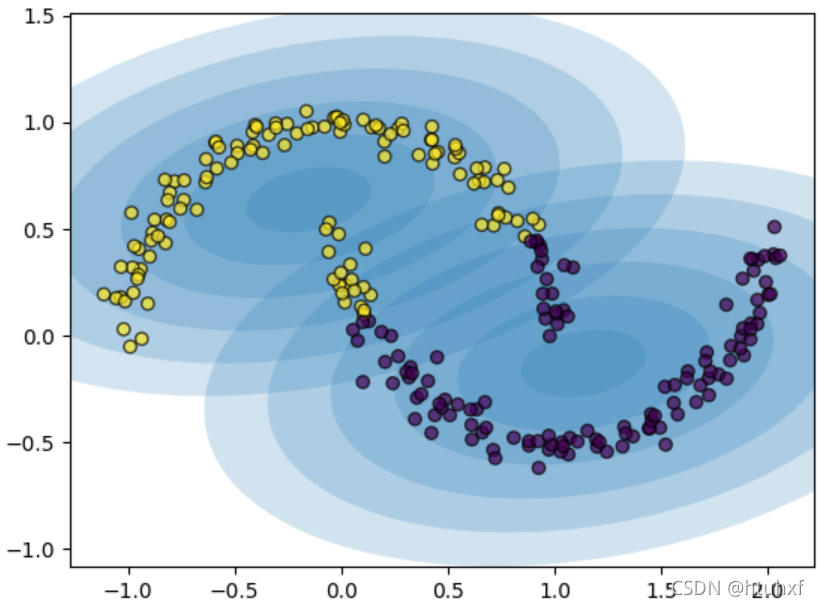
但是，如果我们忽略簇标签，并使用更多的高斯分量（例如16个），GMM可以很好地拟合出这个复杂的数据分布。

gm = GaussianMixture(n_components=16, random_state=0)
plot_gm(gm, Xmoon, label=False)
plt.show()

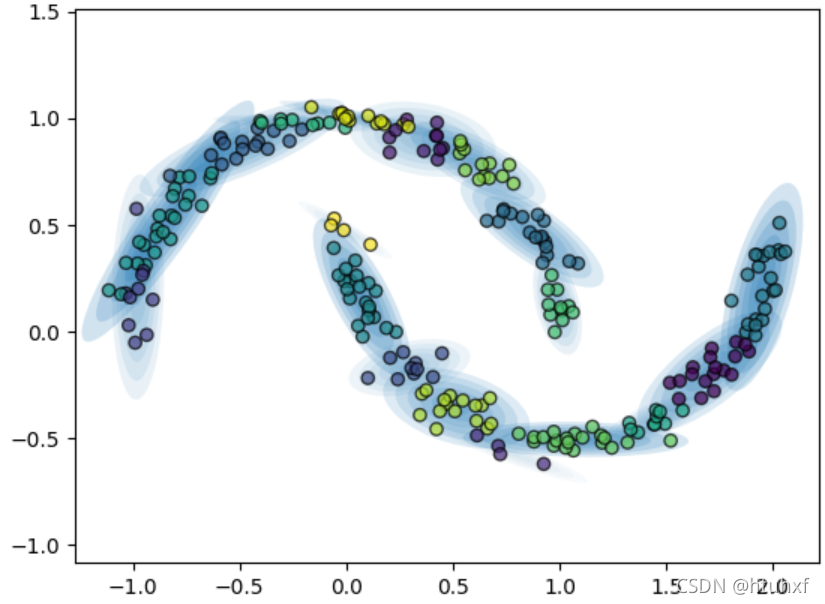
此时的GMM不再是一个聚类器，而是一个描述数据分布的生成模型。我们可以利用它来生成与原始数据分布相似的新样本。

gm = GaussianMixture(n_components=16, random_state=0)
gm.fit(Xmoon)
Xnew, ynew = gm.sample(500)
plt.scatter(Xnew[:, 0], Xnew[:, 1], ec='black', alpha=0.8)
plt.show()

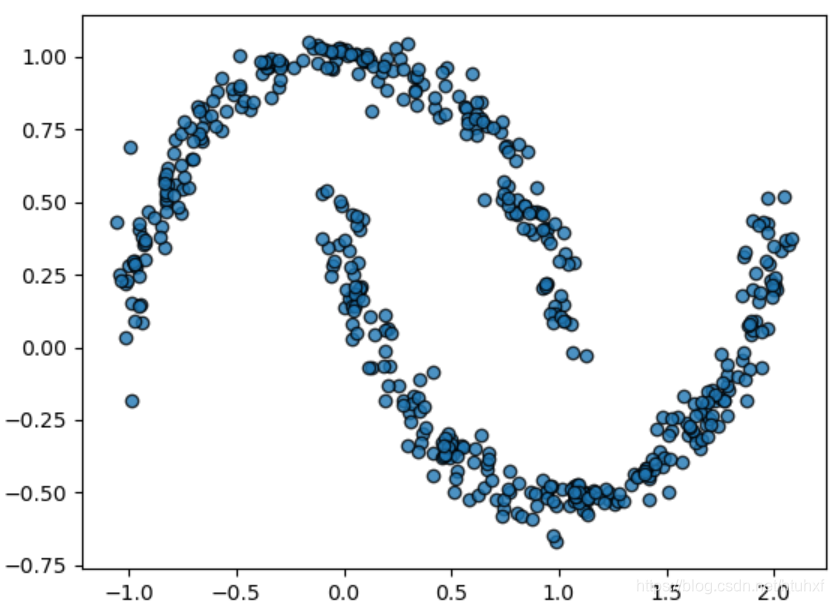
这展示了GMM作为灵活的非参数密度估计工具的强大能力。掌握Python中的这类生成模型，对于数据增强、异常检测等任务至关重要。

五、如何选择组件的数量？

作为一个生成模型，GMM提供了一些客观标准来确定最佳的n_components值。由于生成模型拟合的是数据的概率分布，我们可以评估模型在未见数据上的似然度，或使用信息准则来避免过拟合。两种常用的信息准则是赤池信息量准则和贝叶斯信息量准则。

Scikit-Learn的GaussianMixture对象内置了计算AIC和BIC的方法。

import numpy as np
n_components = np.arange(1, 21)
models = [GaussianMixture(n, random_state=0).fit(Xmoon) for n in n_components]

plt.plot(n_components, [m.aic(Xmoon) for m in models], label='AIC')
plt.plot(n_components, [m.bic(Xmoon) for m in models], label='BIC')
plt.xlabel('n_components')
plt.legend()
plt.show()

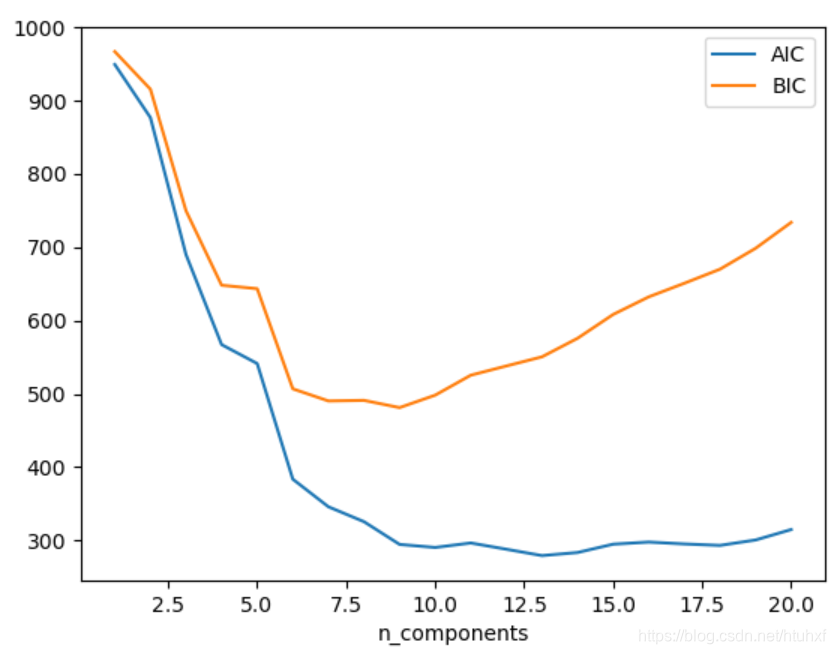
AIC和BIC的值越小越好，它们的形式如下：
$AIC = 2k - 2\ln(L)$
$BIC = k\ln(n) - 2\ln(L)$
其中 $k$ 是模型参数个数，$n$ 是样本数量，$L$ 是模型的最大似然值。两者都在拟合优度（$L$）和模型复杂度（$k$）之间进行权衡，BIC对参数数量的惩罚通常更重。

需要强调的是，通过AIC/BIC选择的n_components是GMM作为密度估计器时的最优值，而不一定是作为聚类算法时的最佳簇数。许多从业者更倾向于将GMM视为一个强大的密度估计工具，仅在数据分布相对简单明确时，才将其用于聚类任务。理解这种区别是掌握这类机器学习算法应用场景的关键。