Python数值求解常微分方程组：树莓派CM0 NANO实战二能级系统与洛伦兹吸引子案例

今天教程介绍了工业树莓派 CM0 NANO 单板计算机结合 scipy 软件包和 Runge-Kutta 算法实现数值求解常微分方程组的项目设计。

项目介绍

工业树莓派 CM0 NANO 单板计算机结合 scipy 与 matplotlib 软件库实现常微分方程组的数值求解。

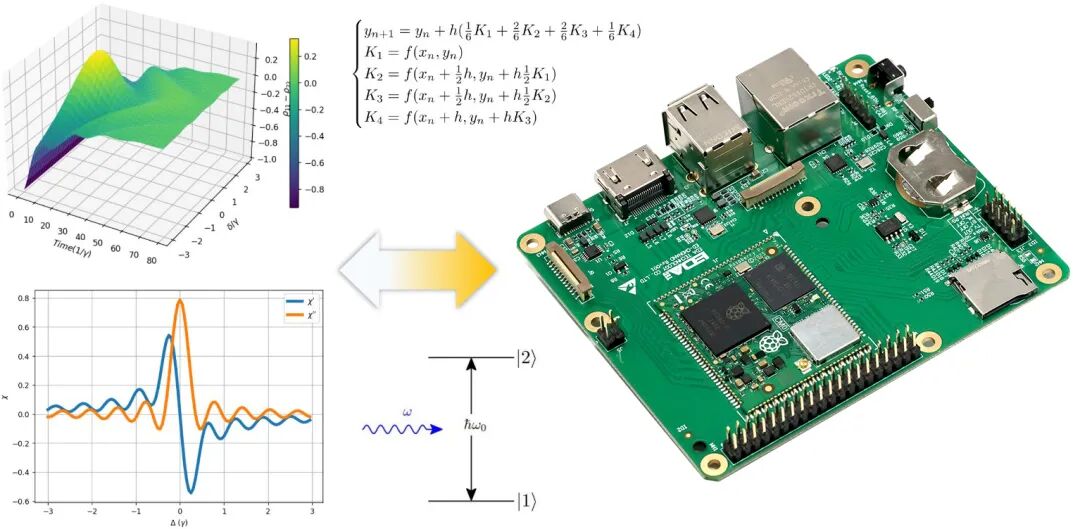
图：三维数值模拟结果与树莓派CM0硬件平台

• 准备工作：硬件连接、系统安装、软件更新等；
• 环境搭建：科学计算所需软件库的安装、数值求解方程组测试等；
• 二能级系统：结合实际物理问题进行数值计算，包括流程图、代码、效果演示等；
• 布居振荡：考虑更为复杂的数值解应用场景，给出粒子 Rabi 振荡动力学及其参数依赖。

准备工作

包括硬件连接、系统安装、软件更新等。

硬件连接

这里使用 SSH 远程登录，仅需要 Type-C 供电和 WiFi 联网。

图：树莓派CM0 NANO开发板实物图

系统安装

开发板需安装树莓派官方最新操作系统，详见： https://www.raspberrypi.com/software/

软件更新

更新软件包

sudo apt update
sudo apt upgrade

环境搭建

安装 scipy 和 matplotlib 软件包，以便调用 RK45 算法和科学绘图；

sudo apt install python3-scipy
sudo apt install python3-matplotlib

Runge-Kutta 算法

为了获得更为精确的数值解，常用方案是采用四阶 Runge-Kutta 方法。

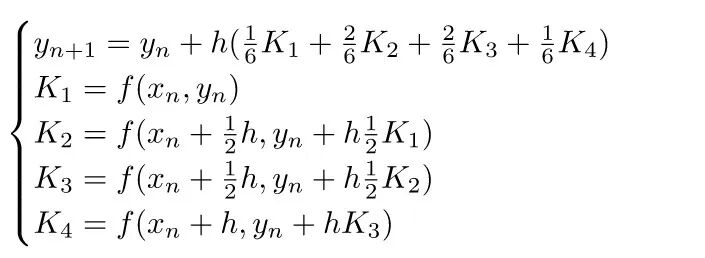
图：数值分析中经典的四阶Runge-Kutta方法公式

详见： http://staff.ustc.edu.cn/~rui/ppt/num/num-ode-rk.html

• 使用 Python 编程，通常采用 odeint 和 solve_ivp 函数实现；

solve_ivp 是 Python 中 SciPy 库提供的一个函数，用于求解初值问题 (IVP, Initial Value Problem) 的常微分方程组 (ODEs)。

使用方法：

scipy.integrate.solve_ivp(fun, t_span, y0, method='RK45', t_eval=None, vectorized=False, args=None, **options)

https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html

数值计算

通过调用 solve_ivp 函数实现常微分方程组的数值求解。

Lorenz 吸引子

Lorenz attractor 是混沌理论中的经典模型，最早由美国气象学家爱德华·诺顿·洛伦兹提出。该模型源于对大气对流方程的简化，旨在研究流体力学中的混沌现象，常用于描述“蝴蝶效应”。Lorenz 吸引子具有三维、非线性和确定性特征，其相轨线呈现出复杂的双纽线形状，状态随时间以非重复模式演变。

其简化的方程形式为

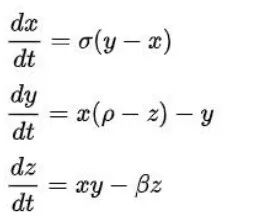
图：描述混沌现象的洛伦兹微分方程组

对于该常微分方程组，可使用 4 阶 Runge-Kutta 算法进行数值求解。

代码

终端执行 touch ode_demo.py 指令新建文件，并添加如下代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# ----------- lorenz equations ------------
def lorenz(t, X, sigma, rho, beta):
    x, y, z = X
    return np.array([
        sigma * (y - x),          # dx/dt
        x * (rho - z) - y,        # dy/dt
        x * y - beta * z          # dz/dt
    ])
# ----------- parameters -------------
sigma = 10.0
beta  = 2
rho   = 30.0
x0    = [1.0, 0.0, 0.5]
t_span = (0, 50)                    # integral range
t_eval = np.arange(0, 50.01, 0.01)  # step 0.01
# -----------  numerical calculation -----------
sol = solve_ivp(lorenz, t_span, x0, args=(sigma, rho, beta),
                t_eval=t_eval, rtol=1e-4, atol=1e-4)
# ---------- plot -----------
fig = plt.figure(figsize=(6, 5))
ax = fig.add_subplot(111, projection='3d')
ax.plot(sol.y[0], sol.y[1], sol.y[2], lw=1.0)
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
ax.set_title('Lorenz Attractor')
plt.show()

效果

终端运行 python lorenz_attractor.py 弹窗显示数值结果

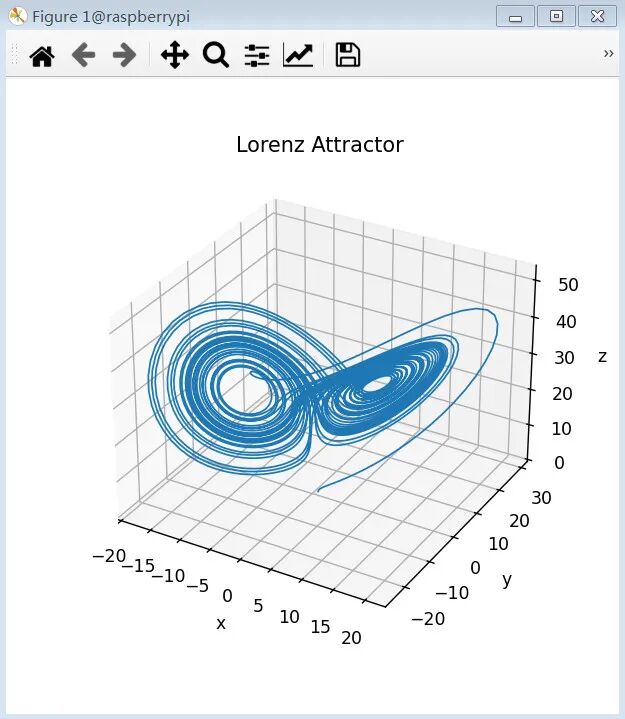
图：使用Runge-Kutta算法数值求解得到的Lorenz吸引子三维图形

使用树莓派 CM0 完全可以胜任常微分方程的求解计算，并获得精确可靠的数值结果。

二能级系统

考虑更为复杂的实际科学计算。这里以量子光学中常见的二能级系统 Liouville 方程组数值求解为例，结合 Python 的 ODE 库函数实现。

Hamiltonian

考虑半经典条件下的光与二能级原子相互作用体系，示意图如下

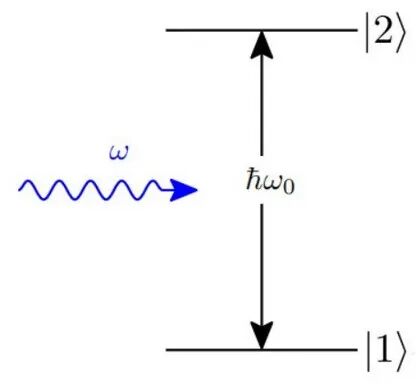
图：二能级量子系统能级跃迁示意图

该系统的 Hamiltonian 可表示为

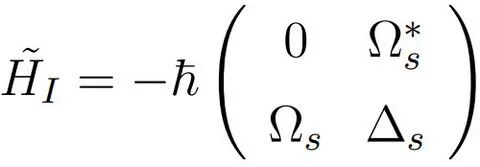
图：二能级系统的哈密顿量矩阵表示

主方程

结合 Maxwell-Liouville 方程（亦称光学 Bloch 方程、 Liouville 方程或密度矩阵主方程），

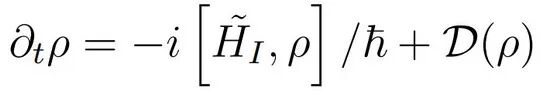
图：包含相互作用与耗散的密度矩阵主方程

给出 Hamiltonian 矩阵元对角元的运动方程

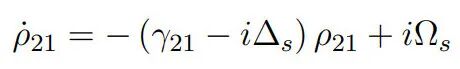
图：二能级系统极化率分量满足的微分方程

该方程组可采用数值或解析的方法求解。

详见：电磁诱导透明机制下基于四波混频过程的光学参量放大动力学研究
http://doi.org/10.27011/d.cnki.gdbsu.2021.001607

代码

终端执行指令 touch sci_two-level_system.py 新建程序文件，添加如下代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# ---------- parameters ----------
Delta   = np.arange(-1, 1, 1)     # delta range
Omega   = 1
gamma21 = 1
t_span  = (0, 1)                    # integral range
R0      = np.array([0.0, 0.0])      # initialize ρ=[ρ1, ρ2]
Nd      = len(Delta)                # number of delta
# ---------- ODE ----------
def rk(t, R, Delta, Omega, gamma21):
    r1, r2 = R
    dr1 = -(gamma21*r1 + Delta*r2)
    dr2 = -(gamma21*r2 - Delta*r1)
    return np.array([dr1, dr2])
# ---------- scan delta ----------
r21R = np.zeros(Nd)   # real χ′
r21I = np.zeros(Nd)   # image χ″
print("Start calculation...")
for m, d in enumerate(Delta):
    sol = solve_ivp(rk, t_span, R0, args=(d, Omega, gamma21),
                    method='RK45', rtol=1e-6, atol=1e-6)
    # get terminal value
    r21R[m] = sol.y[0, -1]
    r21I[m] = sol.y[1, -1]
    # show progress
    if (m+1) % 100 == 0:
        print(f"Process: {m+1}/{Nd} (Delta = {Delta[m]:.1f})")
print("Calculation complete!")
# ---------- Plot ----------
print("Start Drawing...")
plt.plot(Delta, r21R, label=r"$\chi'$", linewidth=4)
plt.plot(Delta, r21I, label=r"$\chi''$", linewidth=4)
plt.xlabel(r'$\Delta$ ($\gamma$)')
plt.ylabel(r'$\chi$')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print("Program Terminate.")

效果

终端运行 python sci_two-level_system.py ，输出计算进度

图：Python脚本在树莓派终端中运行，显示计算进度

弹窗显示稳态结果

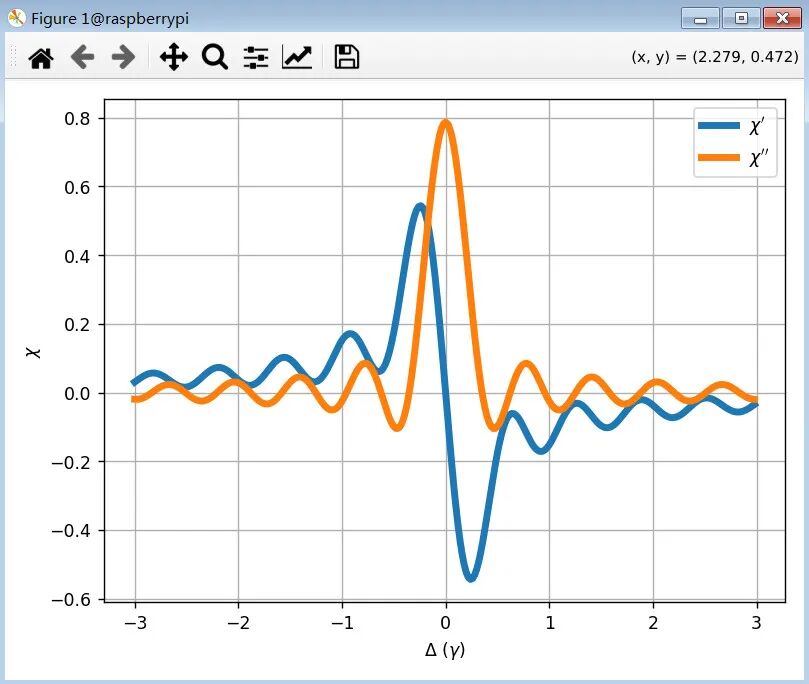
图：二能级系统极化率实部(χ‘)与虚部(χ’‘)随失谐量(Δ)的变化关系

表征介质的吸收（极化率虚部）和色散（极化率实部）特性。

相应的矩阵对角元随时间的演化曲线

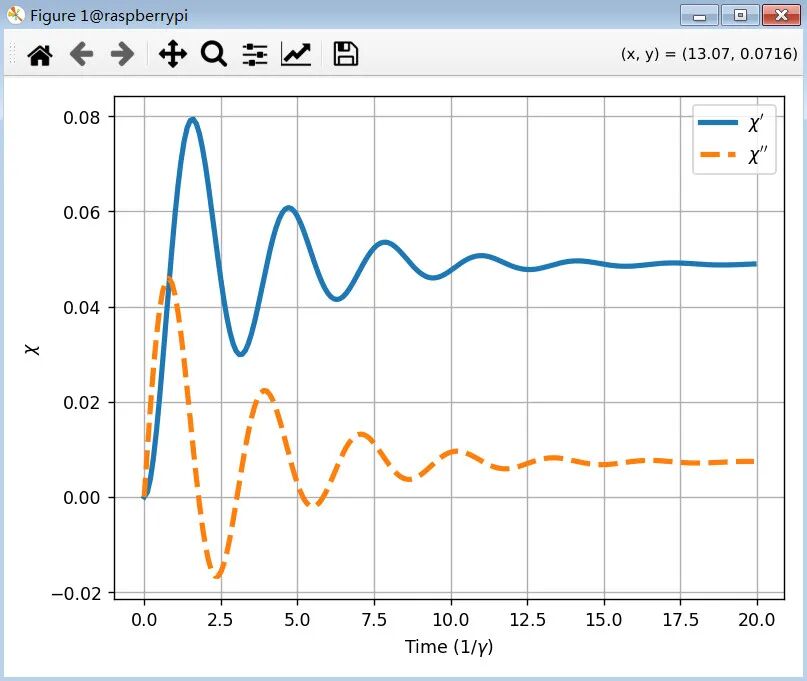
图：介质极化率实部(x‘)与虚部(x’‘)分量随时间演化的曲线

介质极化率随时间演化逐渐趋于稳定。

布居振荡

考虑粒子弛豫情况下的二能级系统 Liouville 方程组的数值求解，同样使用 Runge-Kutta 算法和 solve_ivp 函数实现。

模型

考虑包含耗散的二能级系统，示意图如下

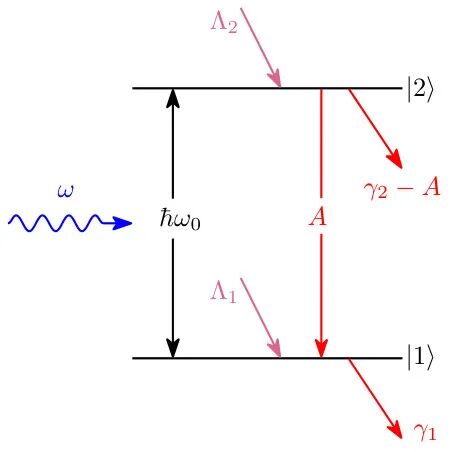
图：包含泵浦与弛豫过程的二能级系统能级图

主方程

结合二能级系统的 Hamiltonian 和密度矩阵的 Lindblad 主方程，可得

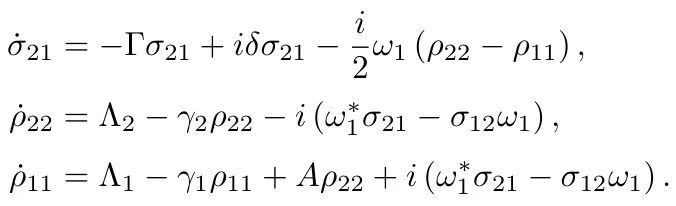
图：描述粒子数布居与相干性演化的方程组

使用 Runge-Kutta 算法，结合 solve_ivp 函数，给出全数值解决方案。

代码

终端执行指令 touch twolevel_pop_t.py 新建程序文件，添加如下代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# ---------- Parameters ----------
omega1 = 1
Lambda1 = 2
Lambda2 = 2
gamma1 = 1
gamma2 = 1
F = 1
Gamma = (gamma1 + gamma2) / 2 + F
A = 1
Dn = np.array([0, 1])             # n
t_eval = np.arange(0, 1, 0.1)     # time range
# ---------- ODE defination ----------
def rk(t, R, delta, omega1, Lambda1, Lambda2, Gamma, gamma1, gamma2, A):
    r11, r22, re21, im21 = R
    dr11 = Lambda1 - gamma1 * r11
    dr22 = Lambda2 - gamma2 * r22
    dre21 = -Gamma * re21 - delta * im21
    dim21 = - Gamma * im21 - omega1
    return np.array([dr11, dr22, dim21])
# ---------- Scan N ----------
P = np.empty((len(t_eval), 4))   # Population
for k, n in enumerate(Dn):
    delta = n * omega1
    R0 = np.array([1.0, 0.0, 0.0, 0.0])  # [ρ11, ρ22]
    sol = solve_ivp(rk, [0, 1], R0, args=(delta, omega1, Lambda2,
                                          Gamma, gamma1, gamma2),
                    t_eval=t_eval, rtol=1e-6, atol=1e-6)
    P[:, k] = sol.y[0, :] - sol.y[1, :]
print("Calculation complete!")
# ---------- Draw ----------
print("Start Drawing...")
plt.plot(t_eval, P[:, 0], '-k',  label=r'$\delta=0$', linewidth=3)
plt.plot(t_eval, P[:, 1], '--r', label=r'$\delta=0.2\gamma$', linewidth=3)
plt.plot(t_eval, P[:, 2], '-.b', label=r'$\delta=0.4\gamma$', linewidth=3)
plt.plot(t_eval, P[:, 3], ':m',  label=r'$\delta=0.6\gamma$', linewidth=3)
plt.xlabel(r'Time ($1/\gamma$)')
plt.ylabel(r'$\rho_{11}-\rho_{22}$')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print("Terminate Program.")

保存代码。

效果

终端运行 python twolevel_pop_t.py ，弹窗显示绘图结果；

• 不同失谐（delta）条件下，粒子布居（ρ11-ρ22）随时间的演化如下
  
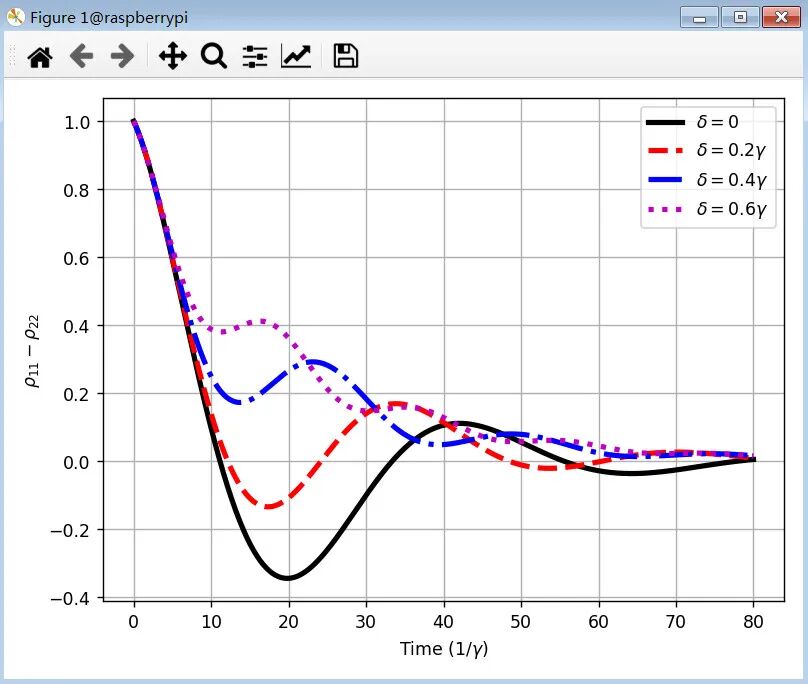
  图：不同失谐参数(δ)下，二能级系统上下能级粒子数差随时间的变化

• 给出布居振荡随时间和失谐变化的伪彩图
  
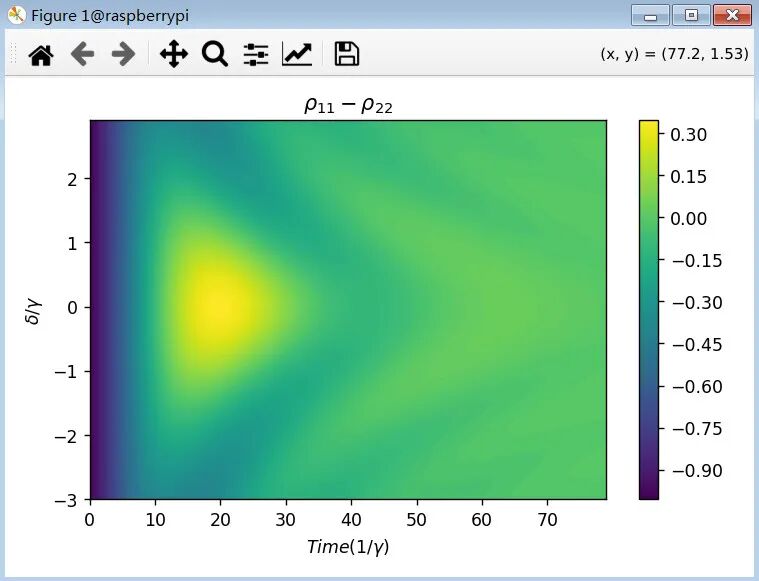
  图：布居差(ρ11-ρ22)随时间和失谐变化的二维热力图

• 给出对应的三维渲染结果
  
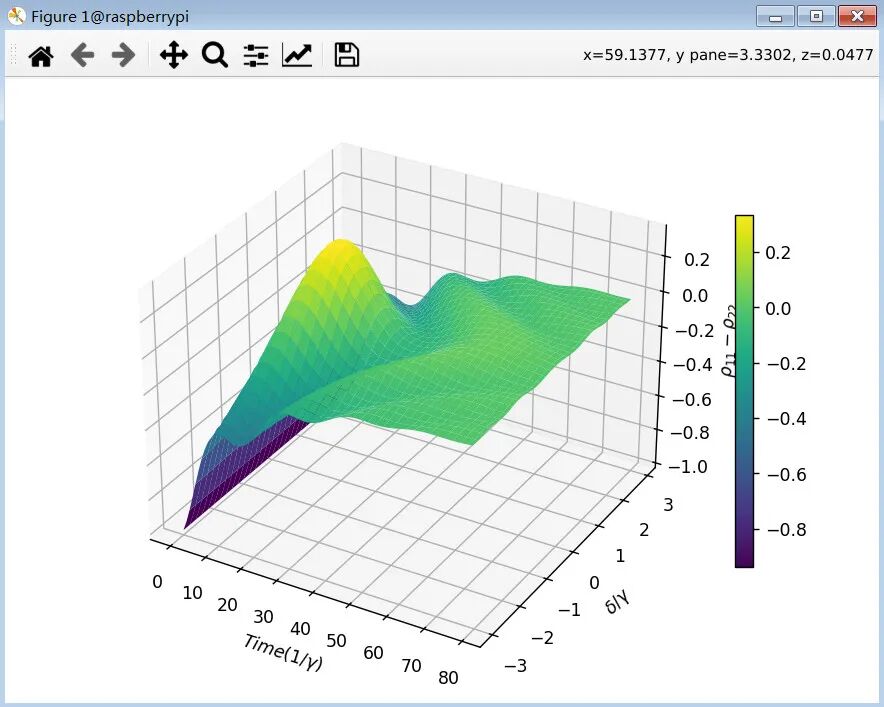
  图：布居振荡随时间和失谐变化的三维曲面图

该结果表明粒子在基态和激发态之间的 Rabi 振荡随失谐的增加而减弱。

总结

本文介绍了工业树莓派 CM0 NANO 单板计算机结合 Python 软件包 scipy 实现常微分方程组的数值求解，给出了该设备在数值计算领域的应用解决方案，包括二能级系统的 Bloch 方程组的数值求解、方程、代码和数值模拟结果，为相关产品在工业、科研、科学计算领域的快速应用提供了参考。

欲了解更多技术实战与开源项目，欢迎访问 云栈社区 交流探讨。