深入解析RC4算法：逆向分析、特征识别与实战破解案例

在密码学中，RC4是一种经典的流加密算法，其密钥长度可变。作为对称加密算法，它加解密使用同一套密钥。RC4曾广泛应用于WEP（有线等效加密）和早期TLS协议中。

流密码同属对称密码体系，但与分组加密不同，它不对明文进行分组处理。其核心在于使用密钥生成与明文等长的伪随机密钥流，然后通过逐字节异或的方式完成加解密。

一、加解密原理

RC4算法主要由伪随机数生成器和异或运算构成。由于其对称性（异或运算的对合性），加密和解密过程完全一致。算法接受可变长度的密钥（1~255字节），并利用它初始化一个256字节的S盒。这个S盒不仅用于生成加密流，其自身状态在加密过程中也会动态变化。

二、加密流程

标准的RC4加密流程可以分为三个关键步骤：

1. 初始化状态向量S：创建一个256字节的数组S，并按升序填充0-255。
2. 初始化临时向量T：根据用户输入的密钥，通过轮转填充的方式生成另一个256字节的数组T。
3. 生成密钥流并加密：基于S和T，通过特定的置换操作生成伪随机密钥流，然后与明文数据进行逐字节异或。

以下是其核心逻辑的伪代码表示：

//1.初始化S和T
for(int i=0;i<255;i++){
    S[i]=i;
    T[i]=K[i%keylen]
}

//2.初始排列S
j=0;
for(int i=0;i<255;i++){
    j=(j+S[i]+T[i])%256;
    swap(S[i],S[j]); //交换S[i]和S[j]
}

//3.产生密钥流，利用密钥流和明文进行加密
i,j=0;
for(int r=0;r<len;r++){
    i=(i+1)%256;
    j=(j+S[i])%256;
    swap(S[i],S[j]);//swap交换
    t=(S[i]+S[j])%256;
    k[r]=S[t];
    data[r]^=k[r];
}

三、C代码实现

为了更好地理解，我们可以将其转换为具体的C语言代码。算法涉及几个基本数据结构：

• S盒：一个256字节的数组，初始为0-255的排列，后续会被密钥打乱。
• 密钥：长度任意的字符数组。
• 临时向量K：长度256字节，用于在初始化阶段轮转存储密钥。

初始化函数

这个函数负责根据密钥初始化S盒。

/*初始化函数*/
void rc4_init(unsigned char*s,unsigned char*key, unsigned long Len){
    int i=0,j=0;
    char k[256]={0};
    unsigned char tmp=0;
    for(i=0;i<256;i++) {
        s[i]=i;  //0-255赋值给s
        k[i]=key[i%Len];  //将k重新计算
    }
    for(i=0;i<256;i++) {  //对s进行初始置换
        j=(j+s[i]+k[i])%256; //给j赋值
        tmp=s[i];
        s[i]=s[j];  //交换s[i]和s[j]
        s[j]=tmp;
    }
}

第一个循环将0-255顺序装入S盒，第二个循环则根据密钥对S盒进行随机化置换。

加解密函数

该函数利用初始化后的S盒对数据进行处理。

/*加解密*/
void rc4_crypt(unsigned char*s,unsigned char*data,unsigned long len){
    int i=0,j=0,t=0;
    unsigned long k=0;
    unsigned char tmp;
    for(k=0;k<len;k++)
    {
        i=(i+1)%256;  //固定方式生成的i
        j=(j+s[i])%256;  //固定方式生成的j
        tmp=s[i];
        s[i]=s[j];  //交换s[x]和s[y]，第二次置换
        s[j]=tmp;
        t=(s[i]+s[j])%256;  //固定方式生成的t
        data[k]^=s[t];  //异或运算
    }
}

该过程是流生成的核心，每处理一个字节都会更新S盒状态并生成一个密钥字节。由于异或的特性，同一函数既可加密也可解密。

示例主函数

#include<stdio.h>
#include<string.h>

int main() {
    unsigned char s[256] = {0};
    char key[256] = {"hello_ctfer"};
    unsigned char data[] = "hello_world";
    unsigned long key_len = strlen(key);

    // 初始化s盒
    rc4_init(s, (unsigned char*)key, key_len);
    // 解密数据
    rc4_crypt(s, (unsigned char*)data, 42);

    // 打印解密后的数据
    for (int i = 0; i < 42; i++) {
        printf("%02x", (data[i]) & 0xff);
    }
    return 0;
}

四、逆向分析

在逆向工程中，识别RC4算法是破解相关程序的第一步。

特征识别

RC4算法通常具备以下特征，便于在反编译代码中识别：

1. 存在多次循环次数为256的for循环。
2. 存在大量取模运算（%256）。
3. 在初始化阶段，有明显的根据密钥打乱一个数组（S盒）的过程。
4. 最终的数据处理环节是简单的异或（XOR）操作。

魔改RC4

出于增加破解难度的目的，出题者常常会对标准RC4进行“魔改”。常见的魔改方式包括：

1. 魔改初始化算法：例如，不将S盒初始化为0-255，或在S盒的初始置换过程中加入额外的可逆运算（如加减固定值）。
2. 魔改加密流程：在生成密钥流或进行异或操作的前后，添加可逆的变换。

图：一段经过魔改的RC4代码，注意其中对S盒的额外操作。

无论如何魔改，算法都必须保持对称加密的核心性质：enc_data = RC4(flag) 且 flag = RC4(enc_data)。

五、实战例题分析

1. 标准RC4识别

题目：2024 Moectf - simple RC4

通过反编译工具（如IDA）查看程序，字符串中直接出现了RC4相关的提示，这强烈暗示了算法类型。

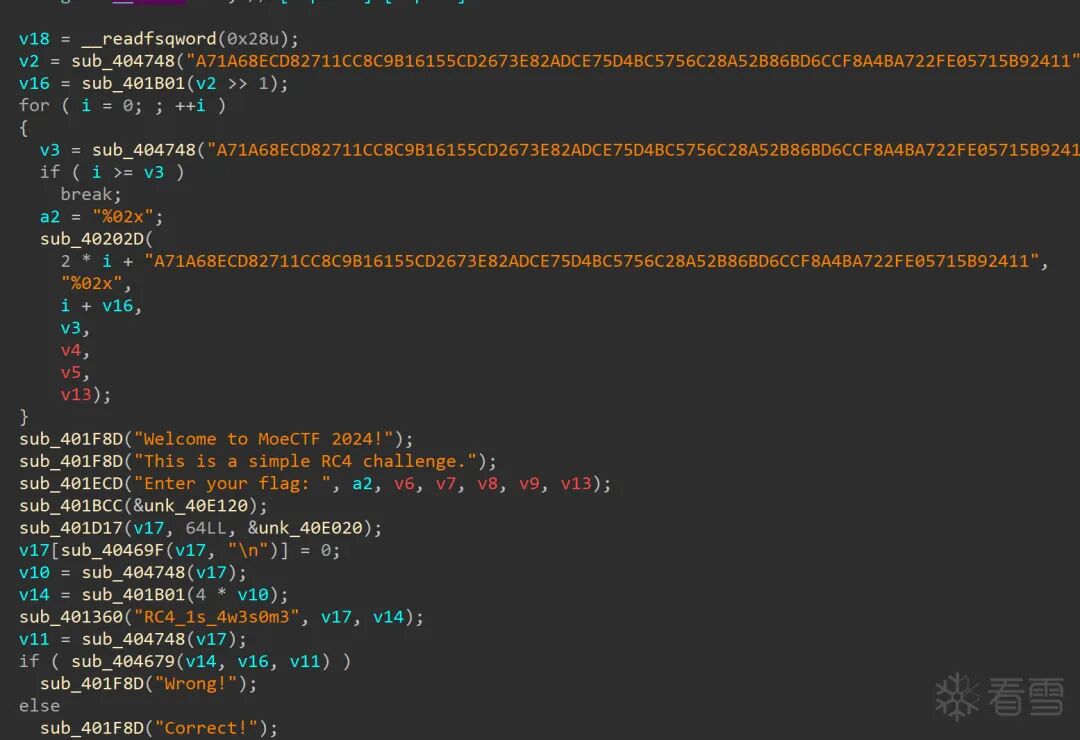
图：在IDA中发现的疑似RC4密钥的字符串。

接下来在数据段或函数中寻找疑似密文的数据，假设其为标准RC4，即可编写解密脚本。

from Crypto.Cipher import ARC4

key = b"RC4_1s_4w3s0m3"
enc = bytes.fromhex("A7 1A 68 EC D8 27 11 CC 8C 9B 16 15 5C D2 67 3E 82 AD CE 75 D4 BC 57 56 C2 8A 52 B8 6B D6 CC F8 A4 BA 72 2F E0 57 15 B9 24 11")

rc4 = ARC4.new(key)
dec = rc4.decrypt(enc)
print(dec)
# 输出：moectf{why_Rc4_haS_The_Rev32sabl3_pr0ceSS}

2. 动态调试破解RC4

题目：2024 极客大挑战 - 让我康康你的调试

当静态分析遇到困难时，动态调试是利器。对于输入长度已知（如33字节）的题目，可以输入等长的测试字符串（如33个a），让程序执行完加密逻辑。

图：使用IDA进行动态调试，程序停在加密函数处。

然后，在内存中提取加密后的数据（即我们的测试字符串a被加密后的结果）。接着，利用调试器插件（如LazyIDA）的“Paste Data”功能，将程序中真正的密文数据粘贴到输入缓冲区，替换掉之前的测试字符串。

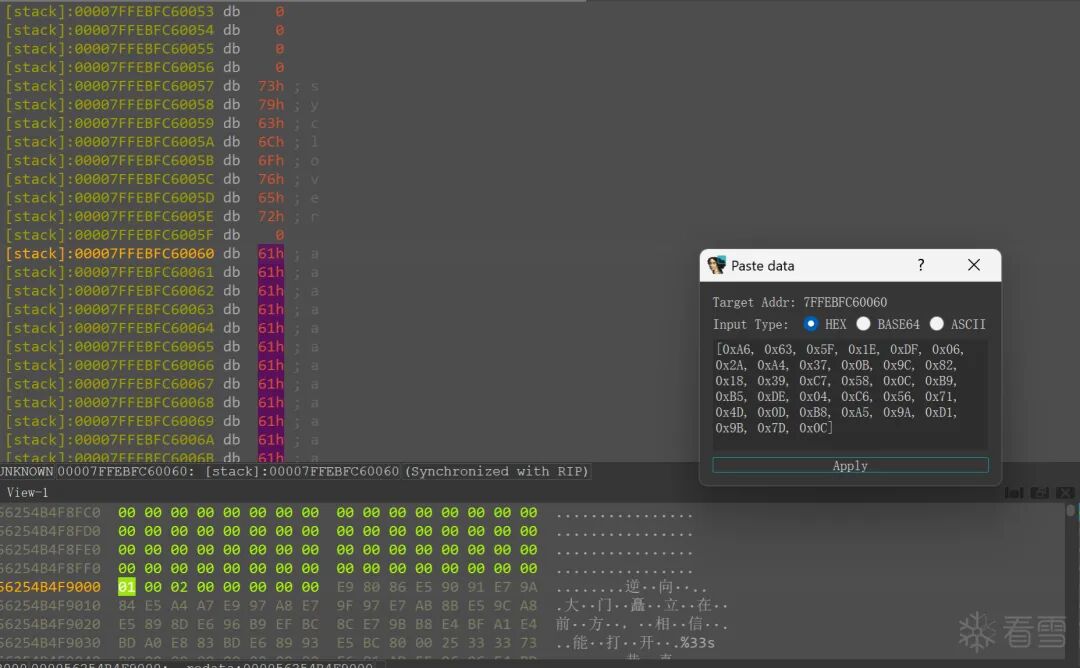
图：通过LazyIDA将提取的密文回填到输入缓冲区。

再次运行程序通过加密逻辑，由于RC4的对称性，原本的密文就会被“解密”成明文，从而直接获得flag。这种方法无需逆向算法细节，巧妙地利用了算法本身的性质。

3. 魔改RC4分析

题目：YLCTF - xorplus

首先通过函数名（如rc4_init, rc4_crypt）判断算法基础。接着，仔细比对初始化函数和加密函数与标准RC4的差异。

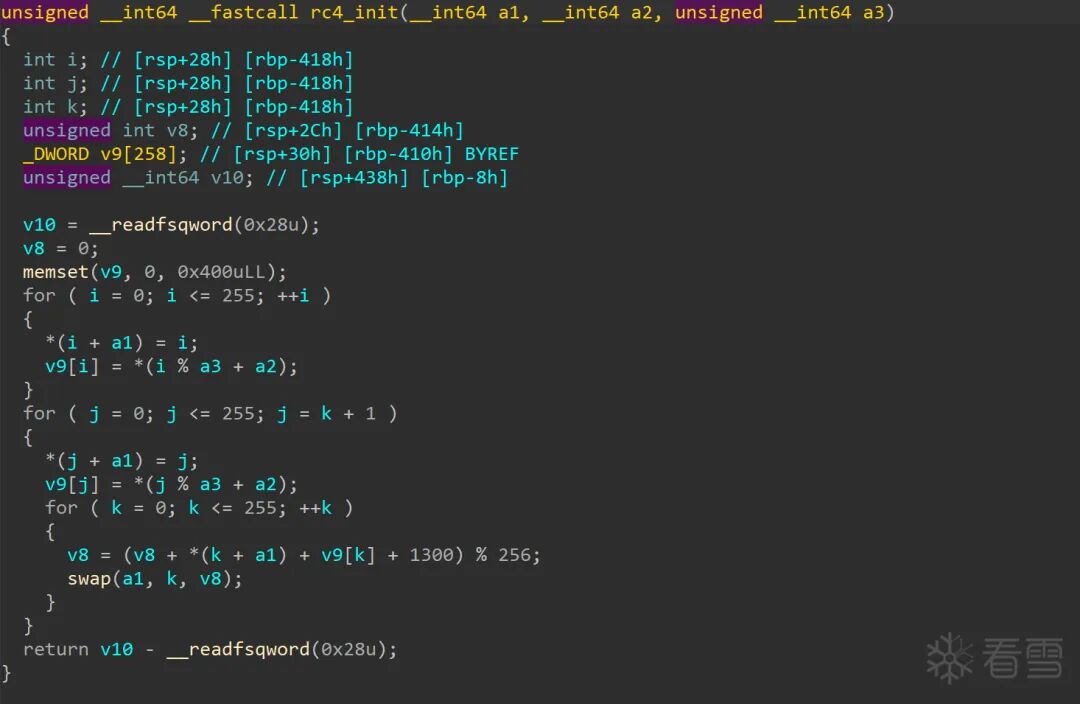
图：初始化函数中增加了 + 1300 的魔改操作。

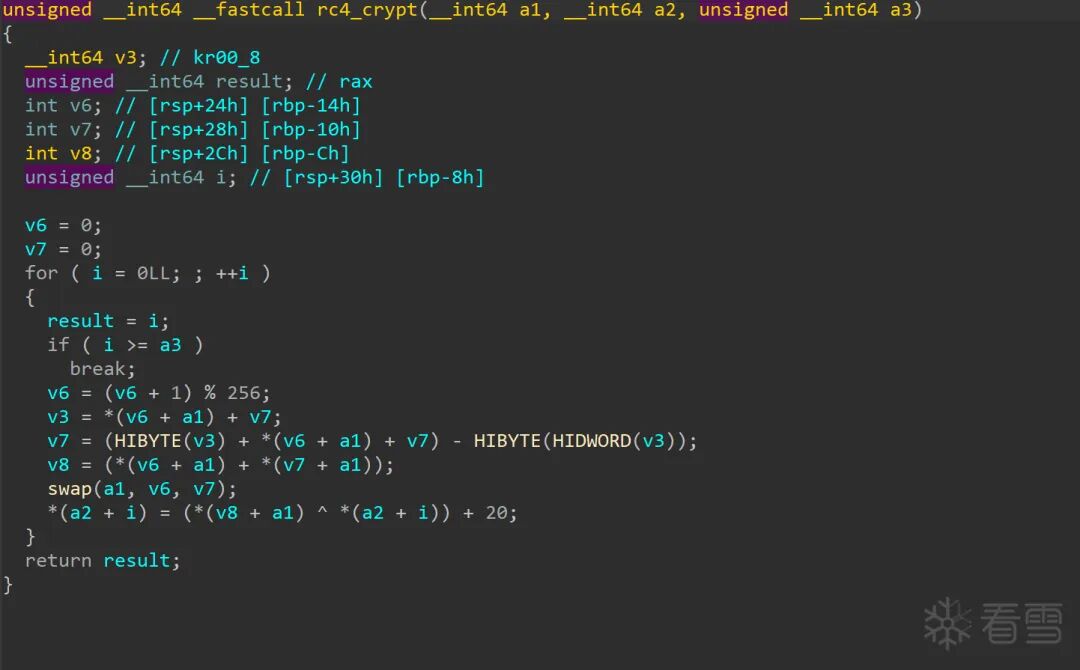
图：加密函数中，异或后还进行了 + 20 的操作。

识别出魔改点后，编写逆向的解密脚本。核心思路是将加密操作逆向：

1. 对于data[k] = (s[t] ^ data[k]) + 20，解密时先-20再^ s[t]。
2. S盒的初始化过程必须与加密端完全一致。

enc = [0x91,0x86,0x1b,0x2d,0x9e,0x6f,0x58,0x31,0x46,0xf0,0xed,0xa2,0xcc,0x90,0x22,0x15,0x8d,0xa2,0x61,0x2d,0x80,0x5a,0x74,0x16,0x6c,0x75,0x81,0x46,0x7e,0x26,0xb5,0x9f,0x85,0x76,0x5d,0xfe,0xb7,0x52,0x54,0xc8,0x4,0x35,0xa6]
s=[0]*256
key="welcometoylctf"
for i in range(256):
    s[i]=i
v6 = 0
for j in range(256): # 复现魔改的初始化
    v6=(ord(key[j%len(key)])+v6+s[j] + 1300)%256
    s[j],s[v6]=s[v6],s[j]

v7 = 0
v8 = 0
for k in range(len(enc)): # 逆向魔改的加密步骤
    v8 = (v8 + 1) % 256
    v7 = (v7 + s[v8]) % 256
    s[v8],s[v7]=s[v7],s[v8]
    enc[k] = (enc[k] - 20) & 0xff # 先减去增加的20
    enc[k] ^= s[(s[v7] + s[v8]) % 256] # 再进行异或

print(bytes(enc))

通过以上对RC4算法从原理到逆向实战的剖析，我们可以看到，无论是标准还是魔改版本，理解其对称性和流程细节都是破解的关键。希望这篇文章能帮助你在云栈社区的CTF之旅或其他安全研究中更好地应对RC4相关的挑战。