
自ResNet提出以来,残差连接因其能有效缓解梯度消失与爆炸问题,已成为构建深度学习模型的基石。然而,简单的单通道残差连接在信息传递的容量上可能存在限制。为此,DeepSeek-AI的研究团队提出了名为“流形约束超连接”(Manifold-Constrained Hyper-Connections, mHC)的新方法,旨在突破这一限制,并在保持训练稳定的前提下,显著提升模型性能。该研究论文《mHC: Manifold-Constrained Hyper-Connections》已于近日发布。
核心摘要:mHC是什么?
- Hyper-Connections (HC):将传统的单条残差流扩展为n条并行通道,从而大幅增加模型的表达能力和性能潜力,但随之而来的是严重的训练不稳定问题。
- mHC的约束:通过将HC中的可学习矩阵投影到“双随机矩阵”(Doubly Stochastic Matrix)构成的Birkhoff流形上,强制模型满足行和与列和均为1的约束。这一巧妙的数学约束将梯度最大增益从HC的约3000倍降至1.6倍,从而实现了27B规模模型的稳定训练。
- 高效工程实现:通过定制的TileLang融合内核、分段重计算策略以及扩展的DualPipe通信重叠技术,mHC(n=4)在27B模型上带来的额外训练时间开销仅为6.7%,内存占用与基线模型基本持平。
- 性能表现:在BBH、DROP、MMLU等8个主流下游评测基准上,mHC全面超越了标准残差连接和原始的HC方法,平均提升约2%。
背景:从标准残差连接到超连接
标准的残差连接(如图1(a)所示)结构简洁,其单层传播公式可表示为:
x_{l+1} = x_l + F(x_l, W_l)
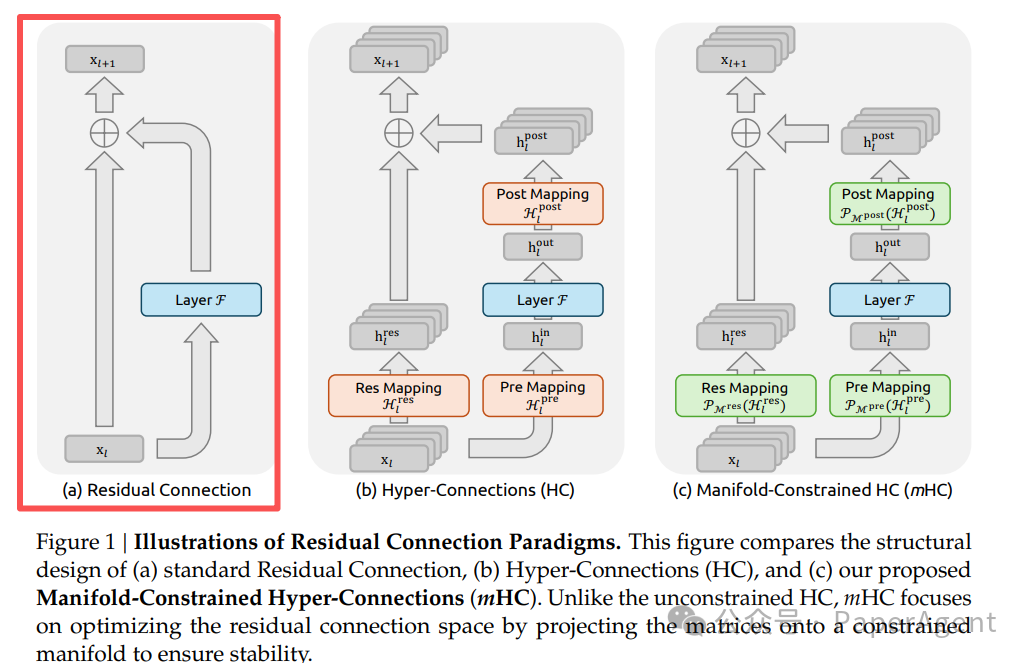
这种恒等映射(identity mapping)的核心优势在于能够维持信号传播的均值和方差大致恒定,从而确保梯度在深层网络中不会爆炸或消失。
为了突破单通道的信息瓶颈,研究者提出了超连接(Hyper-Connections, HC),其结构如图1(b)所示。HC引入了三个可学习的映射矩阵:预映射矩阵 ( H^{pre} )、残差映射矩阵 ( H^{res} ) 和后映射矩阵 ( H^{post} )。单层传播在HC中被定义为:
x_{l+1} = H_{l}^{res}x_{l} + H_{l}^{post}^T F(H_{l}^{pre}x_{l}, W_{l})
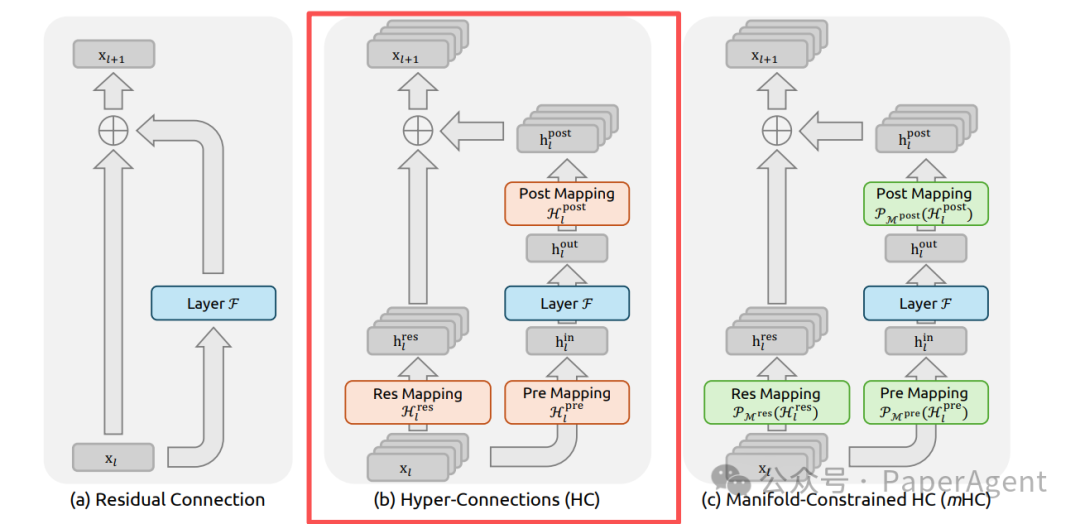

HC带来的问题:
- 数值不稳定:由于映射矩阵 ( H^{res} ) 无约束,多层复合映射 ( \prod H^{res} ) 不再保持恒等映射的特性,可能导致前向信号或反向梯度的增益急剧变化(峰值可达3000倍),引发训练崩溃。
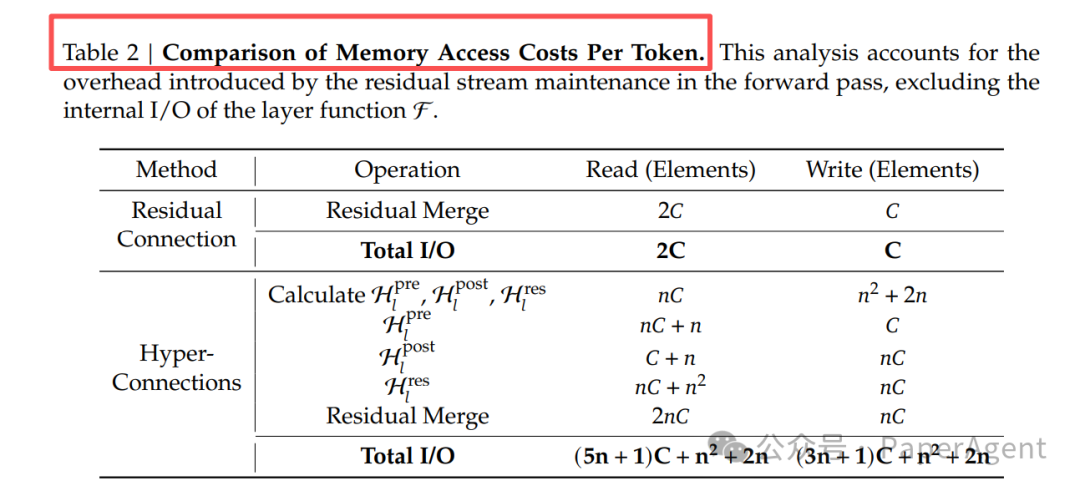
- 系统开销剧增:多通道操作导致内存访问量(I/O)大幅增加,约为原来的n倍(如表2所示),同时加剧了模型并行训练中的流水线气泡。
mHC核心:将矩阵约束在双随机流形上
mHC(Manifold-Constrained HC)的核心思想是为HC中的自由矩阵套上“缰绳”。如图1(c)所示,它通过数学约束确保训练的稳定性。
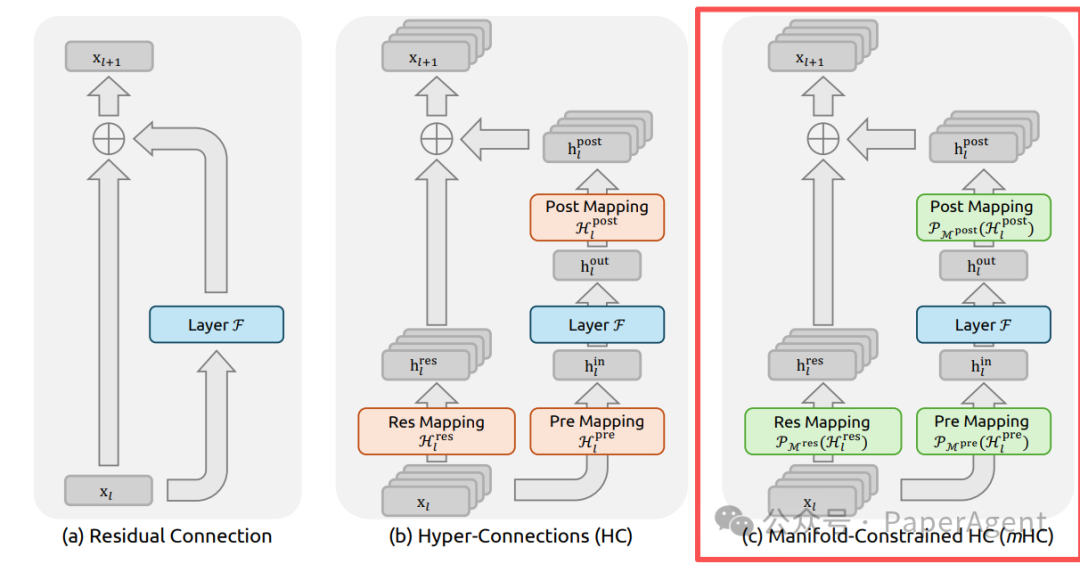
双随机矩阵的稳定特性
mHC将关键的残差映射矩阵 ( H^{res} ) 约束为双随机矩阵(所有元素非负,且每行、每列元素之和均为1)。这种矩阵具备三大优良特性:
- 均值保持:行和与列和为1,能像标准残差连接一样,保持信号传播的均值稳定。
- 谱范数有界:其谱范数(最大奇异值)小于等于1,这从根本上遏制了梯度爆炸。
- 乘法封闭性:多个双随机矩阵的乘积依然是双随机矩阵,这意味着无论网络多深,复合映射的稳定性依然有保障。
实现方式:Sinkhorn-Knopp投影
如何将一个普通的无约束矩阵变成双随机矩阵?研究采用了经典的Sinkhorn-Knopp算法。该算法通过交替进行行归一化和列归一化(通常只需约20次迭代),就能快速地将一个矩阵投影到双随机流形上,其计算开销相对于整个Transformer层的计算可以忽略不计。
此外,为了保证非负性,预映射和后映射的输出会经过Sigmoid函数处理,确保输入到后续计算的值均为非负,避免正负抵消破坏稳定性。
高效的工程实现:如何将开销控制在6.7%
引入额外的映射和约束必然会带来计算开销。mHC通过一系列精妙的系统优化,将这部分开销降到了最低。
1. TileLang融合内核
将RMSNorm、矩阵乘法以及Sinkhorn投影的20轮迭代等多个操作,融合编译成仅3个定制化内核(Kernel)。这种融合极大地减少了中间结果在GPU显存中的读写次数,将I/O带宽压力降低了约70%。
2. 分段重计算
为了节省激活值缓存所需的内存,采用了分段重计算策略。每 ( L_r ) 层只保存第一层的输入,该段内后续层的激活值在反向传播时现场重新计算。研究发现,理论最优的 ( L_r ) 值与流水线并行的阶段(Pipeline Stage)长度天然对齐,实现了内存与计算效率的平衡。
3. 扩展的DualPipe通信重叠
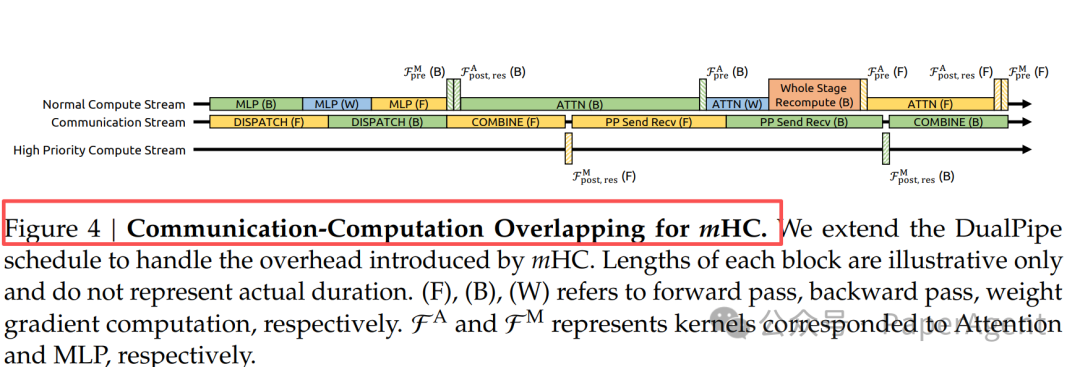
在多流(Multi-Stream)调度中,将计算密集的FFN后映射(post-mapping)内核分配至高优先级流,使其计算能够与必要的通信操作充分重叠。如图4所示,这种优化使得通信与计算的重叠率超过90%,有效隐藏了mHC引入的额外开销。
实验结果:稳定性、扩展性与性能全面领先
训练稳定性
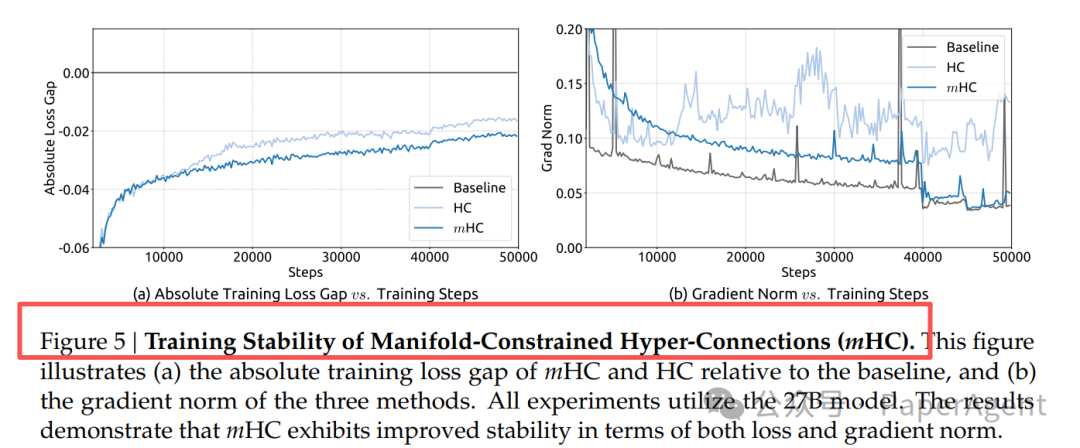
如图5所示,在27B模型的训练过程中,mHC的绝对训练损失与基线(Baseline)的差距始终保持在极低水平(约0.021),且其梯度范数全程平稳。相比之下,原始的HC方法则表现出较大的损失波动和剧烈变化的梯度范数,验证了mHC在稳定训练方面的有效性。
缩放定律
图6展示了mHC的扩展特性。无论是在不同计算预算下的模型扩展曲线,还是在固定模型大小下的数据扩展曲线,mHC都表现出比基线更优的性能,表明其是一种更高效的架构改进。

传播稳定性
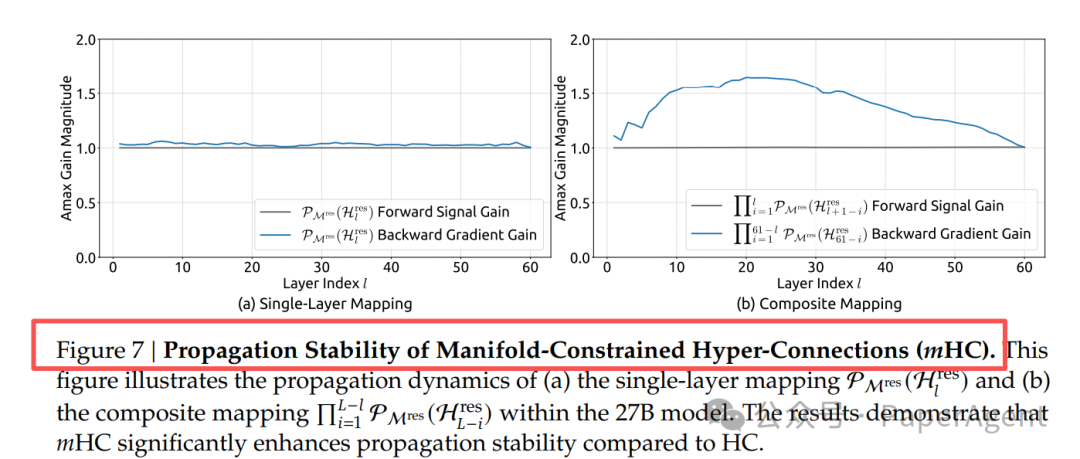
图7从信号传播角度揭示了mHC稳定性的根源。在单层和多层复合映射中,mHC的前向信号增益和反向梯度增益都被严格约束在1附近,而HC的增益则会出现巨大波动。这直观证明了双随机矩阵投影的约束作用。
下游任务性能
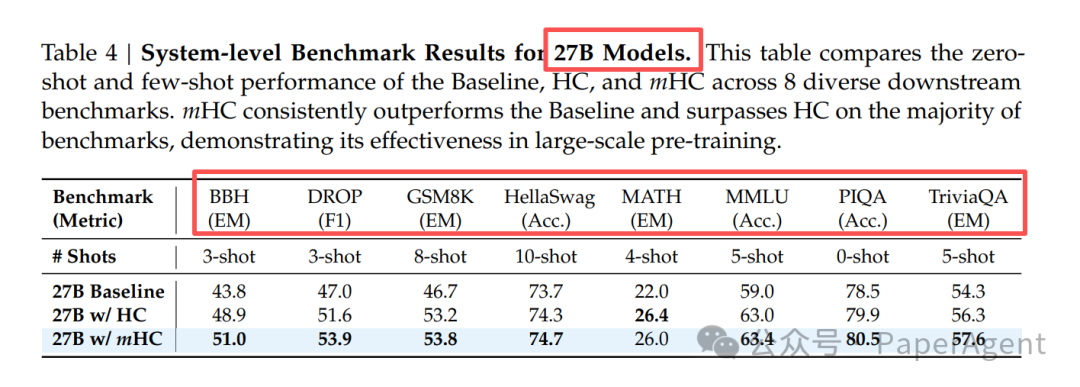
如表4所示,在27B模型规模下,mHC在BBH、DROP、GSM8K、MMLU等8个多样化的下游评测基准上,其零样本/少样本性能全面超越了基线模型和HC模型。例如,在BBH(精确匹配)上相比HC提升2.1%,在DROP(F1分数)上提升2.3%,充分证明了其在大规模预训练中的有效性。
技术比喻
我们可以用一个简单的比喻来理解这三种连接方式:
- 标准残差连接:像一条单车道乡村公路。车流(数据)稳定,从不堵车也不出事故(梯度稳定),但通行容量有限。
- 超连接 (HC):将单车道扩建成四车道高速公路。车道多了,理论上车流通行能力(模型性能)暴增。但由于没有交通规则,车辆可以随意变道、超速甚至逆行,最终导致连环车祸(梯度爆炸),交通瘫痪(训练崩溃)。
- 流形约束超连接 (mHC):同样是一条四车道高速公路,但在每个入口和出口都设置了智能流量控制系统(双随机矩阵约束)。它确保进入每条车道的车辆数等于驶出的车辆数,并且车速被合理限制。这样,既大幅提升了通行效率,又杜绝了重大事故,保证了整个路网的稳定运行。工程师们还将这套控制系统做得非常高效(定制化内核与调度),使得司机通过收费站(额外计算)的等待时间仅增加了6.7%。
总结与资源
DeepSeek-AI提出的mHC方法,通过将数学上的流形约束思想与精密的系统工程相结合,成功解决了超连接架构的训练不稳定难题。它在几乎不增加额外开销的前提下,为大规模深度学习模型提供了一条稳定提升性能的新路径。这项研究不仅展示了一个有效的架构改进,其背后的稳定性分析方法和系统优化策略也为未来的神经网络结构设计提供了宝贵参考。
论文链接:
https://arxiv.org/pdf/2512.24880
论文标题:mHC: Manifold-Constrained Hyper-Connections
对深度学习模型架构创新和训练优化感兴趣的朋友,欢迎在云栈社区分享你的见解,与更多开发者一同探讨前沿技术。