标题:Tail risk exposure and the cross section of expected stock returns
作者: Maxime L.D. Nicolas (University College London)
发布日期:2026年1月9日
文章主要研究了股票对市场尾部事件的敏感性(即尾部风险敞口,TRE)是否能获得风险溢价。作者指出,现有的TRE估算方法通常受到市场总体相关性(correlation)的严重干扰。实证发现,尾部风险仅在低相关性的股票中被定价,并据此提出了一种新的双重排序投资策略。
1. 引言
背景:许多研究认为投资者需要对市场崩盘或尾部事件的敞口进行补偿,因此高尾部风险敞口(TRE)的股票应获得更高的预期收益。
问题:尾部依赖(Tail Dependence)通常是在资产与市场本身就具有很强联动性(高相关性)的环境下估算的。因此,测得的TRE很大一部分可能反映的是相关性,而非纯粹的尾部风险。
2. 资产定价中的尾部风险敞口分析
这一部分主要通过理论和模拟探讨了尾部依赖系数(Tail Dependence Coefficient, TDC)的定义及其估算陷阱。
定义与估算:介绍了TDC的定义,即在市场发生极端损失的条件下,个股发生极端损失的概率。
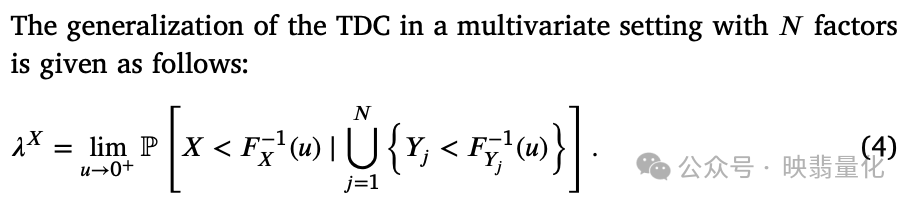
相关性的陷阱(Pitfalls):
- 理论偏差:通过下图展示了高斯Copula(无尾部依赖)和Clayton Copula(有尾部依赖)的区别。但在高相关性下,即使是无尾部依赖的模型(如高斯),非参数估算方法也会错误地检测出显著的尾部依赖。
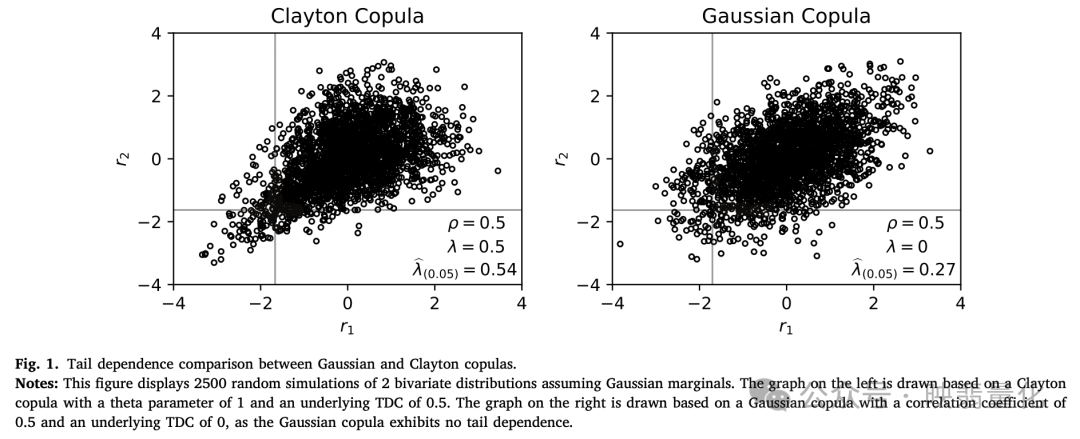
- 与相关系数的内在关系:通过下图展示在不同自由度(ν)下,TDC 与相关系数 ρ 的关系;即使“真正的尾部依赖不强”,只要相关性高,估计出来的 TDC 也会很大。
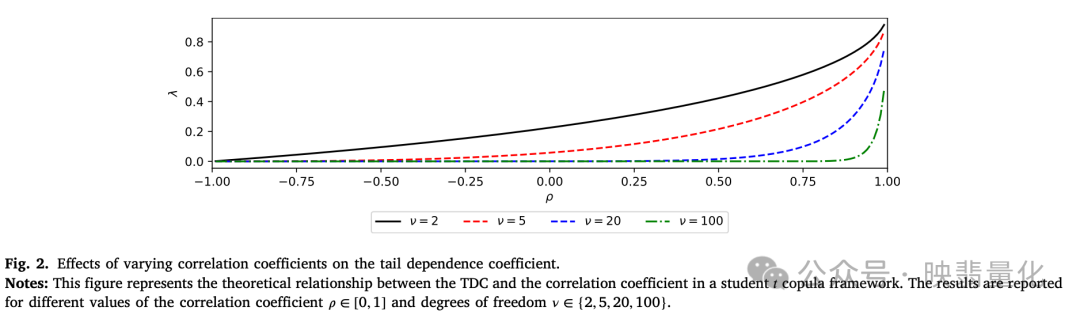
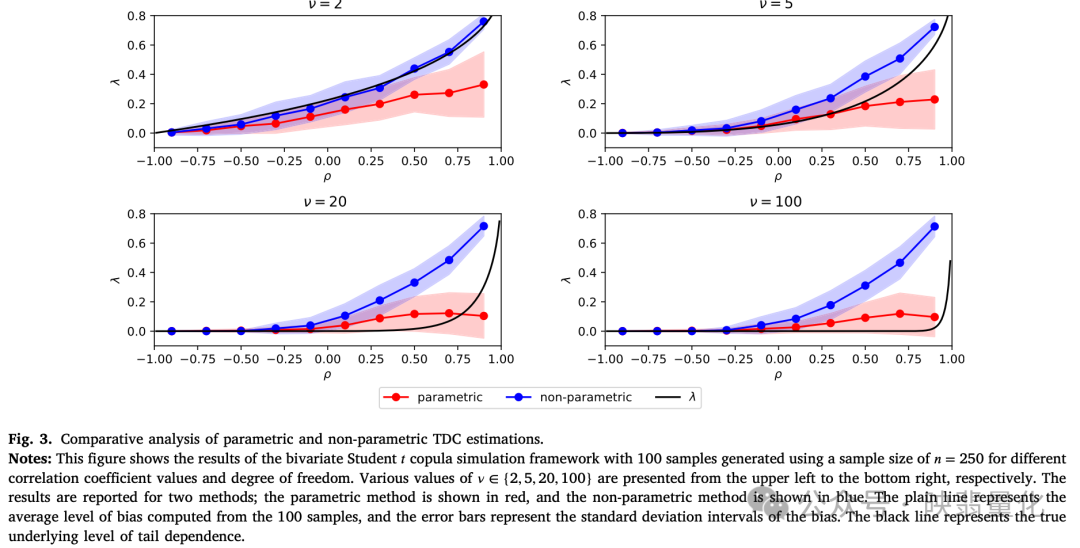
- 模拟实验:下图显示了参数法和非参数法在不同相关性水平下的表现。结果表明,当总体相关性较高时,估算偏差显著增加,导致出现“虚假”的尾部风险读数。这意味着高相关性股票的TRE往往被高估。
3. 数据与变量
- 数据来源:使用CRSP数据库中的美股数据(1964年1月至2023年12月);NYSE / AMEX / NASDAQ 普通股;剔除低价股和流动性差的股票;月度样本量约1800–6000 只股票。
- 主要TRE变量:

4. 实证结果
4.1 统计描述与演变
- 统计特征:非参数 TDC(λ̃)均值明显高于参数法,非参数方法更容易“放大”尾部风险;TRE指标与相关系数(ρ)之间存在很强的正相关性,这证实了TRE估算中包含大量线性依赖成分。
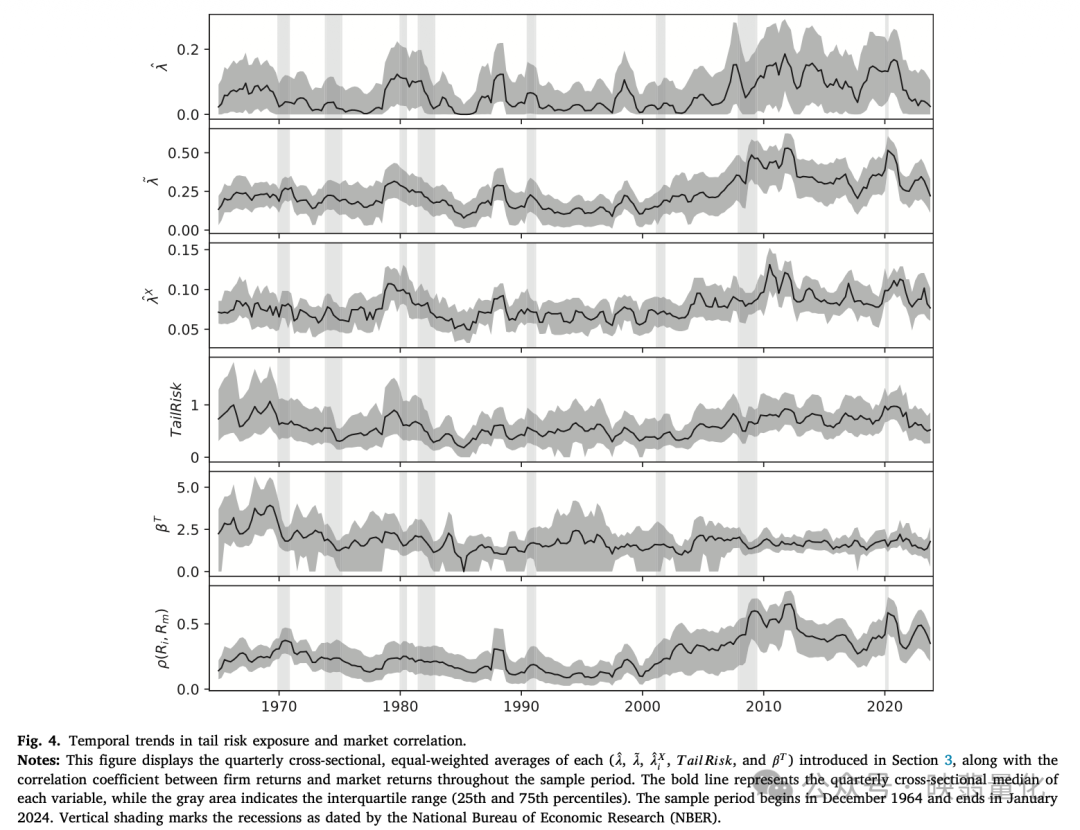
- 时间趋势:下图展示了TRE指标随时间的演变,在市场危机期间(如1987、2008、2020)会出现显著峰值。
4.2 单变量投资组合排序
作者首先仅根据TRE指标将股票分为10组,构建多空投资组合。
结果显示并不稳健:虽然某些指标(如 λ̂、λ̃、λ̂ᵢˣ)显示出正向的风险溢价,但其他指标(如 TailRisk、βᵀ)甚至显示出负向或不显著的溢价。这表明单纯依靠TRE无法持续捕捉风险溢价。
4.3 双变量投资组合排序 —— 本文核心发现
为了剥离相关性的影响,作者采用了双重排序法:首先根据相关性将股票分为5组,然后在每个相关性组内再根据TRE分为5组。
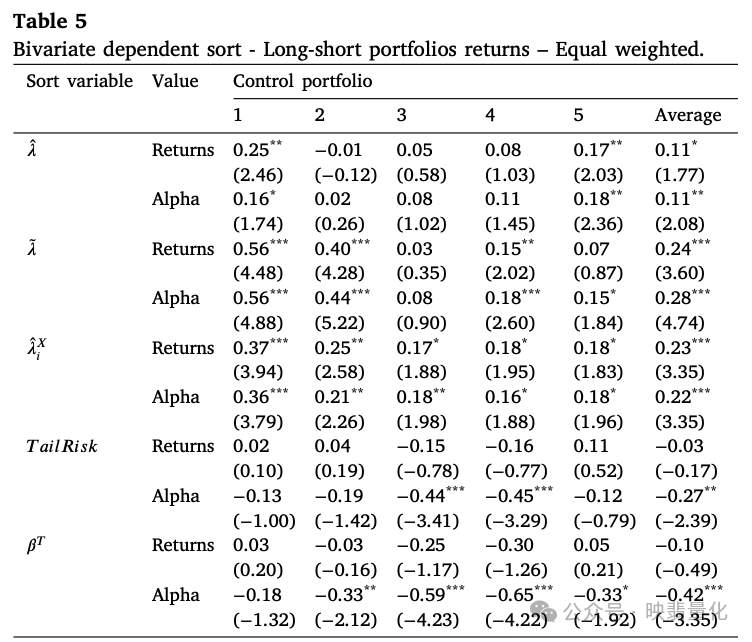
下表展示了控制相关性后的结果:在高相关性组别中,TRE带来的超额收益不显著。这表明对于高相关性股票,投资者可能已经高估了其风险,或者TRE仅仅是相关性的代理变量;在低相关性组别中,TRE策略产生了显著且强劲的正向超额收益(Alpha)。
结论:尾部风险溢价主要由低相关性股票驱动。在低相关性股票中,投资者往往低估了尾部风险(因为这些股票平时与市场不联动),一旦发生极端事件,价格调整会带来显著收益。
4.4 Fama-MacBeth 回归
通过回归分析进一步证实,一旦加入相关系数作为控制变量,许多TRE指标对未来收益的预测能力就会大幅下降甚至消失。这再次证明了区分“一般相关性”和“纯粹尾部风险”的重要性。
4.5 双重排序策略
基于上述发现,作者构建了一个具体的交易策略:只在低相关性股票池中,做多高TRE股票、做空低TRE股票。
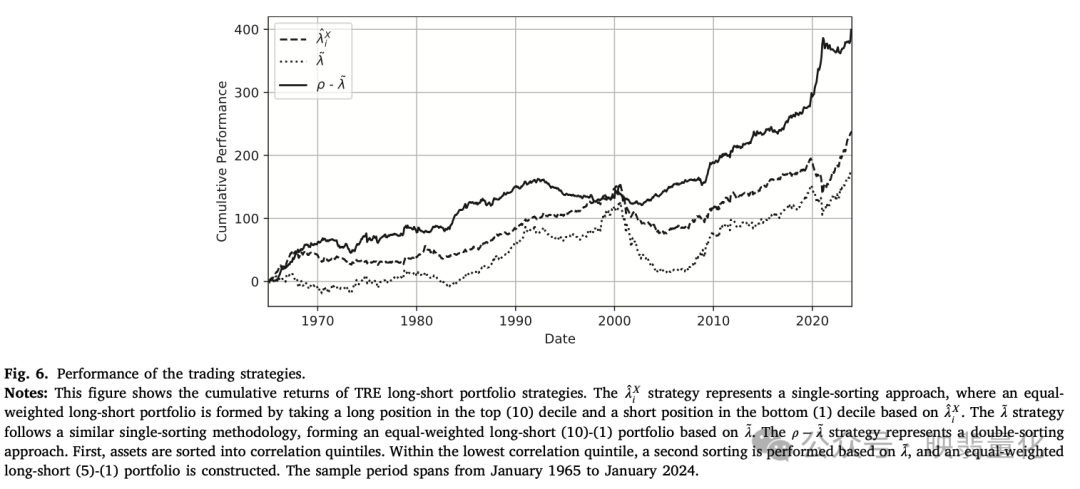
- 下图比较了该策略与传统单变量策略的累计收益。
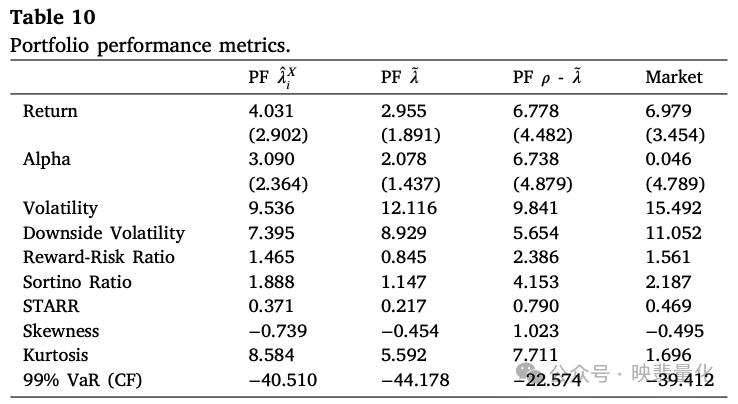
- 绩效指标表明双重排序策略的年化超额收益(6.78%)和夏普比率远高于单变量策略,且最大回撤更小。该策略有效地利用了低相关性股票中被错误定价的尾部风险。
5. 结论
TRE并不是一个独立的预测因子,其有效性高度依赖于估算方法和市场相关性水平。 投资者倾向于高估高相关性股票的尾部风险(或者是估算偏差导致),而低估低相关性股票的尾部风险。这种认知偏差为在低相关性股票中构建基于尾部风险的量化策略提供了机会。对于希望深入研究此类 数据科学 方法的开发者,可以参考 云栈社区 上的相关讨论和资源。
相关资源:
|