Prim算法详解：C++实现最小生成树与洛谷P3366模板题解析

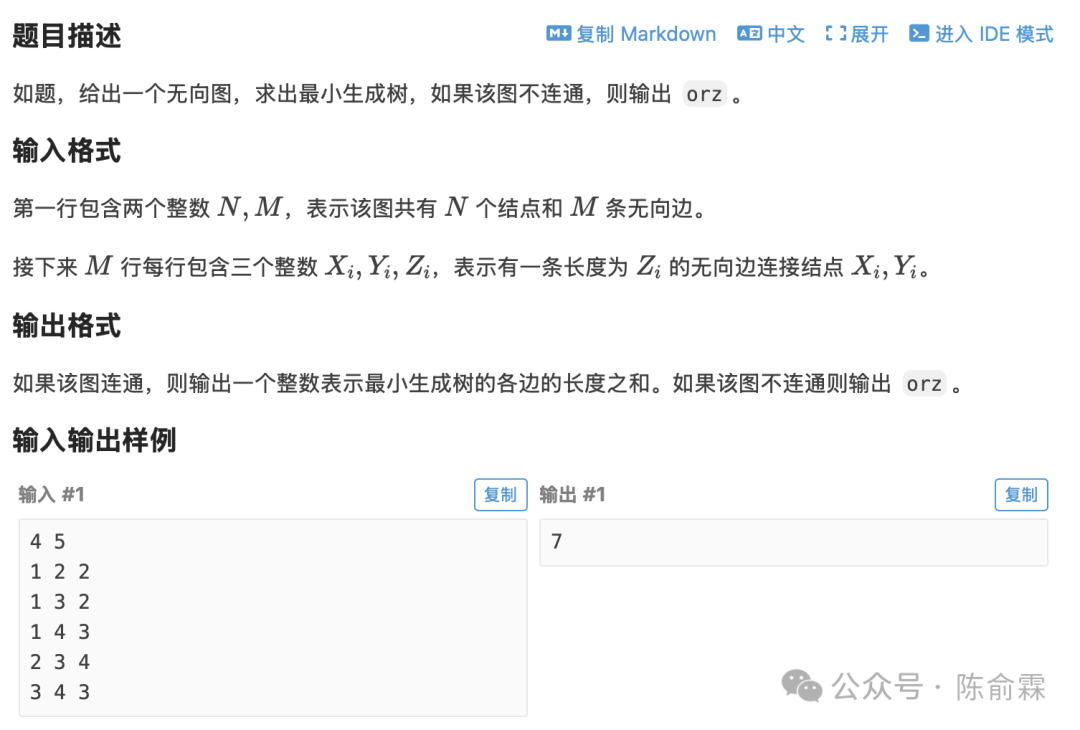
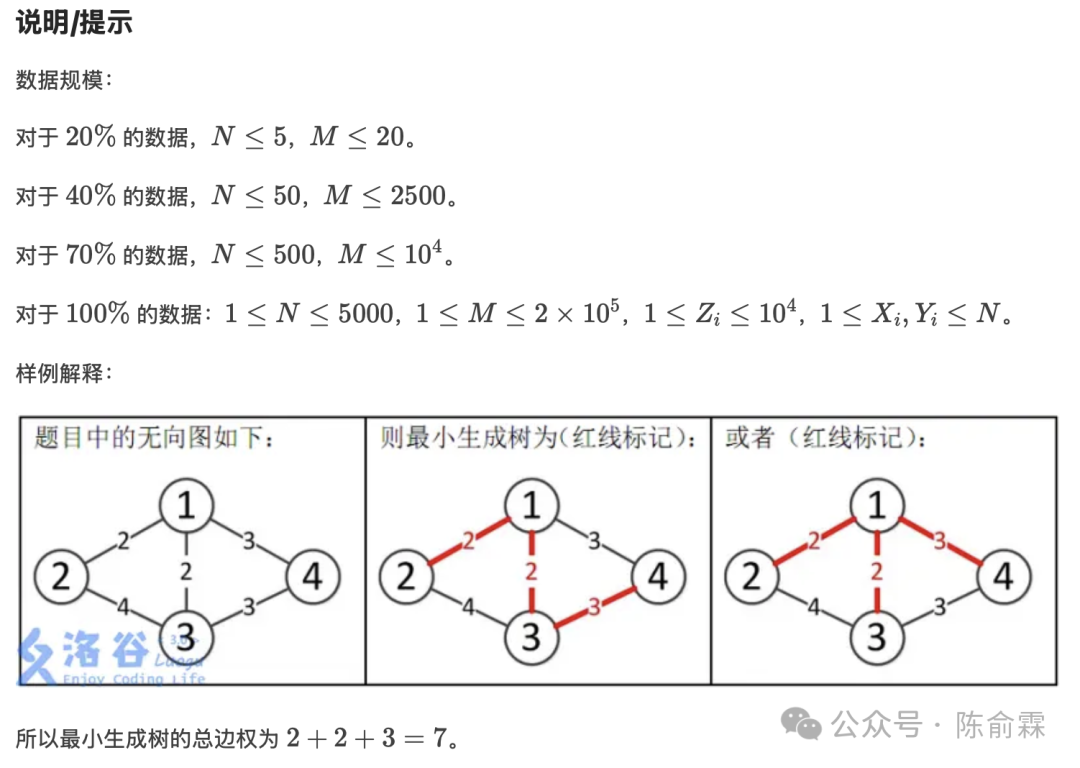
本文将讲解使用 Prim 算法解决加权无向图的最小生成树 (MST) 问题，并提供针对洛谷 P3366 模板题的 C++ 实现代码。Prim 算法是图论中解决 MST 问题的经典贪心算法之一。

Prim 算法核心思想

Prim 算法用于寻找加权无向图的最小生成树。其核心采用贪心策略，从图中任意一个顶点出发，逐步扩展生成树。在每一步中，它总是选择连接“已加入生成树的顶点集合”和“未加入生成树的顶点集合”的权值最小的边，并将该边及其连接的另一个顶点纳入生成树中，直到所有顶点都被包含。

算法步骤详解

1. 初始化：选择一个起始顶点（通常为 1 号顶点），将其加入最小生成树集合，并初始化一个优先队列（或数组）来维护候选边。
2. 扩展生成树：重复以下步骤，直到所有顶点都被加入生成树集合：
   • 选择边：从优先队列中取出连接生成树集合与非生成树集合的、权值最小的边。
   • 加入顶点：如果这条边连接的另一个顶点尚未在生成树中，则将该顶点加入生成树集合，并将这条边的权值累加到总权和中。
   • 更新候选边：遍历这个新加入顶点的所有邻接边，将那些连接着未访问顶点的边加入优先队列，作为新的候选边。
3. 结束判断：如果成功将全部 N 个顶点加入生成树，则得到最小生成树的总权值；否则，说明原图不连通。

Prim vs Kruskal：算法比较

• Prim（普里姆算法）：基于顶点扩展。通常使用优先队列（二叉堆）或简单的数组来维护当前最短边。在稠密图中表现良好，使用二叉堆优化后的时间复杂度为 O(E log V)。
• Kruskal（克鲁斯卡尔算法）：基于边排序。首先将所有边按权值排序，然后使用并查集来判断是否形成环。其时间复杂度主要来自排序，为 O(E log E)。

对于邻接矩阵存储的稠密图，朴素的 Prim (O(V²)) 可能更简单；对于边数较少的稀疏图，使用优先队列的 Prim 和 Kruskal 都是常用选择。

C++ 代码实现（邻接表 + 优先队列）

以下代码采用了邻接表存储图，并使用 priority_queue（最小堆）来高效选取最小权值边，以此解决洛谷 P3366 模板题。

#include<bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII; // pair<权重, 顶点>
vector<PII> g[5005]; // 邻接表
bool vis[5005]; // 标记顶点是否已加入MST

int prim(int n){
  memset(vis,0,sizeof(vis));
  priority_queue<PII,vector<PII>,greater<PII>> q; // 最小优先队列

  int vertexCount = 0; // 已加入MST的顶点数
  int totalWeight = 0; // 最小生成树的总权值和

  q.push({0, 1}); // 从1号顶点开始，初始边权为0

  while(!q.empty() && vertexCount < n){
    int currentWeight = q.top().first;
    int currentNode = q.top().second;
    q.pop();

    if(vis[currentNode]) continue; // 该顶点已在MST中，跳过
    vis[currentNode] = true;
    totalWeight += currentWeight;
    vertexCount++;

    // 遍历当前顶点的所有邻接边
    for(auto &edge : g[currentNode]){
      int neighborNode = edge.first;
      int edgeWeight = edge.second;
      if(!vis[neighborNode]) q.push({edgeWeight, neighborNode});
    }
  }

  if(vertexCount == n) return totalWeight; // 图连通，返回总权值
  else return -1; // 图不连通
}

int main(){
  int n, m;
  cin >> n >> m;

  // 构建无向图的邻接表
  for(int i = 0; i < m; i++){
    int u, v, w;
    cin >> u >> v >> w;
    g[u].push_back({v, w});
    g[v].push_back({u, w});
  }

  int result = prim(n);

  if(result == -1) cout << "orz" << endl;
  else cout << result << endl;

  return 0;
}

代码要点解析：

• 数据结构：g 是邻接表，g[u] 存储与顶点 u 相连的所有 (顶点v, 边权w) 对。vis 数组标记顶点状态。
• 优先队列：priority_queue<PII, vector<PII>, greater<PII>> 定义了一个最小堆，队首元素总是权重最小的 (weight, node) 对。
• 贪心过程：while 循环是算法主体。每次弹出最小边，若其指向的顶点未访问，则加入 MST 并累加权重，同时将该顶点的所有外向边加入优先队列。
• 连通性判断：最终通过 vertexCount 是否等于 n 来判断图是否连通。

掌握 Prim 算法及其实现，对于理解贪心策略在图论中的应用至关重要。更多算法学习资源和讨论，欢迎访问云栈社区。