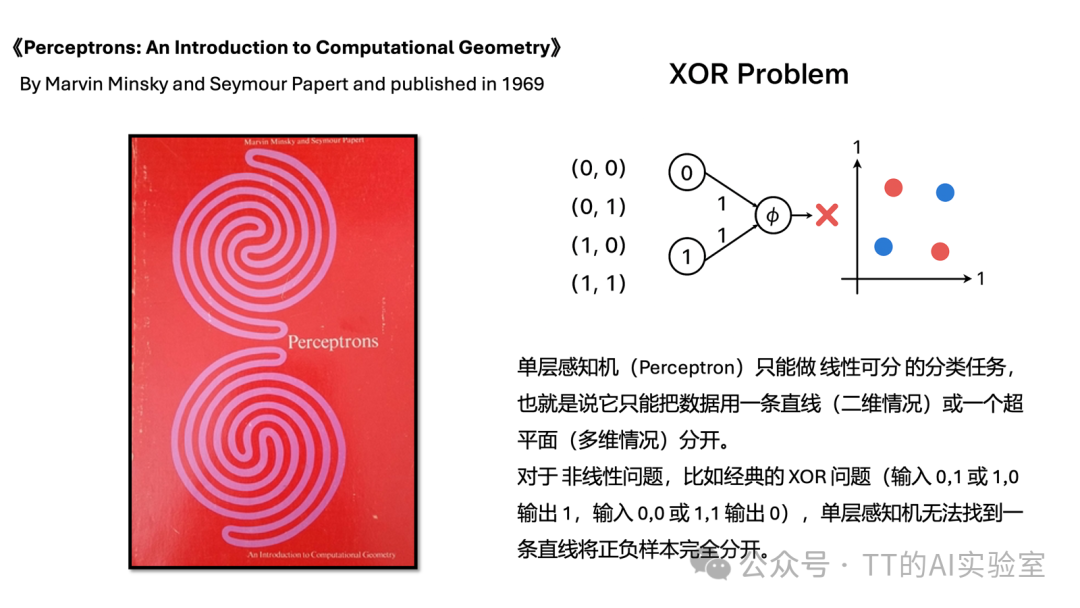
有个更现实的问题:就算你有再好的“下山策略”(优化方案),如果模型本身只是简单的“线性分类器”,它的表达能力仍然有上限。面对复杂、非线性的数据,线性模型就像一辆只能直线行驶的车,地形一旦交错复杂,就会显得力不从心。
因此,这一篇我们要迈出关键一步:从“怎么优化参数”,转向“模型架构本身”。我们将正式进入神经网络的世界,看看如何通过线性运算与非线性激活函数的组合,逐步构建表达能力更强的模型,从而去拟合和刻画复杂、多变的真实世界问题。
一、从线性模型到神经网络
回顾我们之前讨论的线性分类器(f=Wx),它本质上就是只有一层的神经网络。
如果把分类任务比作在数据平面上划分领地,线性分类器更像一把“直尺”:只能直来直去地划出一道分界线。然而面对图像分类这类复杂任务,不同类别的数据往往像乱麻一样缠绕在一起。只靠一把直尺画出的直线,根本无法把它们干净利落地分开。
这就是神经网络(Neural Network)登场的时候。它不再满足于只划一道直线,而是通过增加层数(layers)和非线性(Non-linearity),去勾勒出更灵活、更复杂的决策边界。
结构重组:从单层架构到多层神经网络
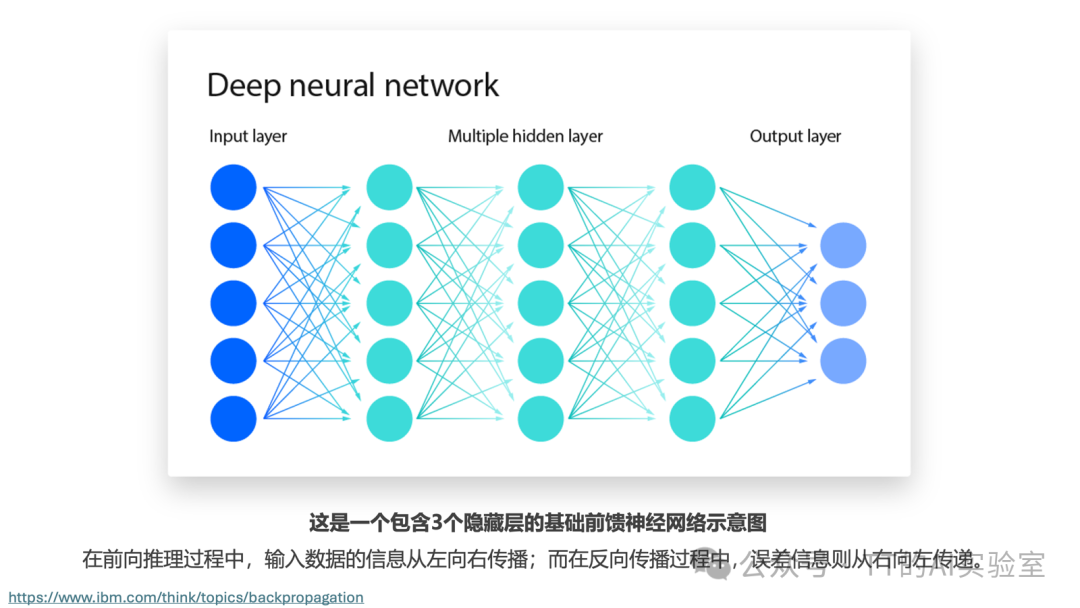
当我们不再一步到位,而是在输入与输出之间加入隐藏层(Hidden Layer)时,模型就从单层架构进化成了多层神经网络。这种层级化(Hierarchical)的结构,是通往“深度学习”的第一步。
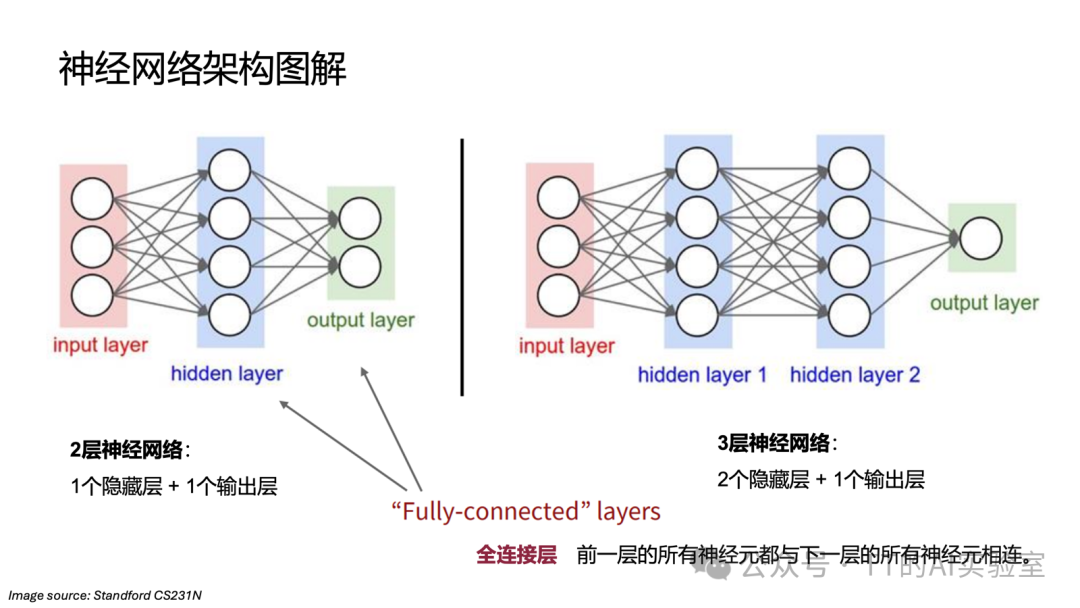
在神经网络中,隐藏层之所以叫“隐藏”,是因为我们(外部观察者)看不到它直接接收原始数据,也看不到它直接给出最终答案。但它非常关键:如果说输入层是“眼”,输出层是“嘴”,那么隐藏层更像“大脑的思考过程”。
二、隐藏层的意义:逻辑的深度与“模板”的进化
从线性分类器到深度神经网络,不只是数学公式变长了,更是模型理解能力的质变。
线性分类器(f=Wx)试图一次性跳过所有逻辑,直接从像素得出结论。而神经网络通过嵌套结构,构建了更完整的推导链条:
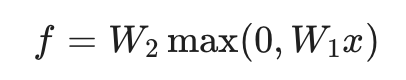

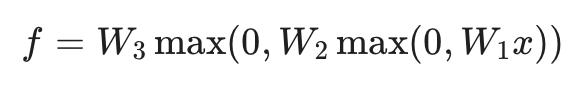
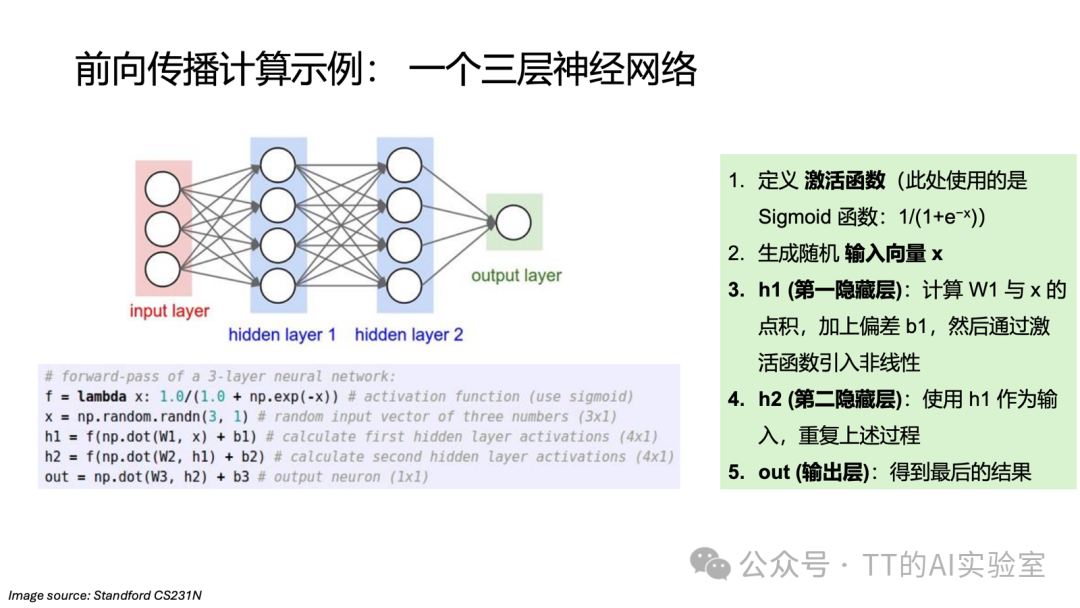
注:实际工程中,每一层都会引入偏置项(Bias)b 以提升平移不变性。为简化逻辑,此处暂不列出。
这种嵌套结构带来了核心价值的质变,可以从三个维度理解。
在线性分类器中,每一类只能学习一个“标准模板”。而隐藏层实现了特征的复用与多样化:

- 第一层(W1)的任务是“分解”:把原始像素映射到多个隐藏神经元上。每个神经元会探测某种局部特征,比如简单边缘、线条、色块。
- 激活函数(max)的任务是“筛选”:只有当输入图像包含某个神经元感兴趣的特征时,该神经元才会被激活。
- 第二层(W2)的任务是“组合”:输出层不再直接看像素,而是看哪些隐藏层“模板”被激活了。
核心突破点:隐藏层让模型不再是为“猫”或“狗”各记一张图,而是学习成百上千个通用的视觉组件。不同类别共享这些底层模板,这种特征复用(Sharing templates between classes)正是深度学习能够精准建模复杂数据的关键。
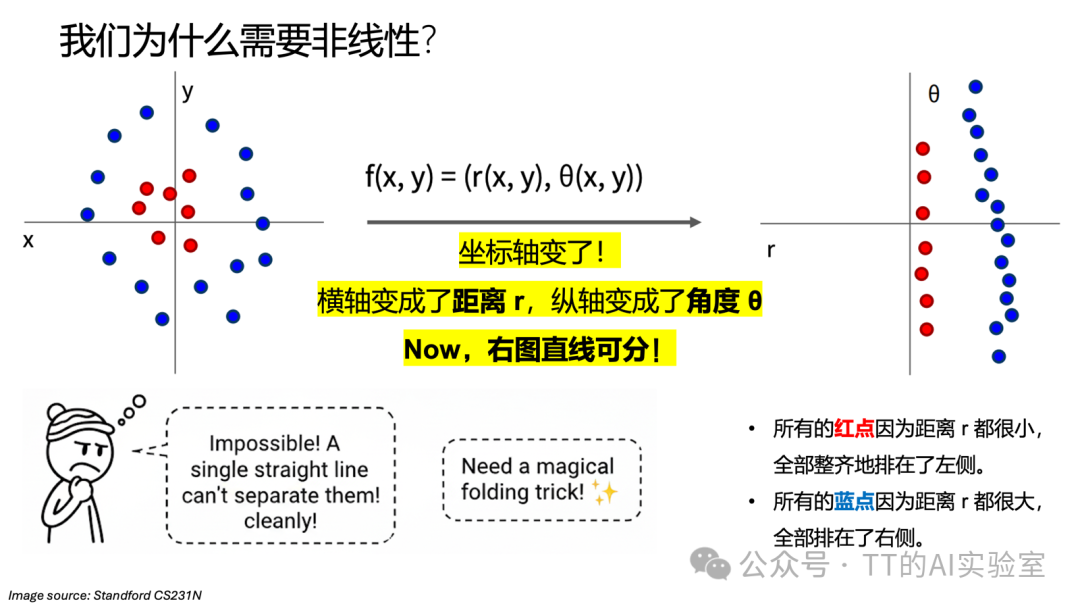
2)非线性变换(Non-linearity):实现空间折叠
在数学层面,隐藏层利用激活函数(如 ReLU)对原始数据空间进行“扭曲”或“折叠”。
想象数据分布像一张揉皱的纸,线性分类器这把“直尺”无法把它切开。隐藏层在做的事情,本质上是不断把这张纸“摊平”。经过层层变换,原本纠缠不清的数据在特征空间中变得整齐可分,最终让输出层只需“一刀”即可分类。
3)构建层层递进的推导算路:跨越“语义鸿沟”(Semantic Gap)
图像的底层数据是像素(0-255 的数字矩阵),而最终分类标签是抽象语义(如“猫”“车”)。像素与语义之间存在巨大的鸿沟:单一像素的改变(光照变化、平移等)并不会改变语义,但会彻底改变输入数据。
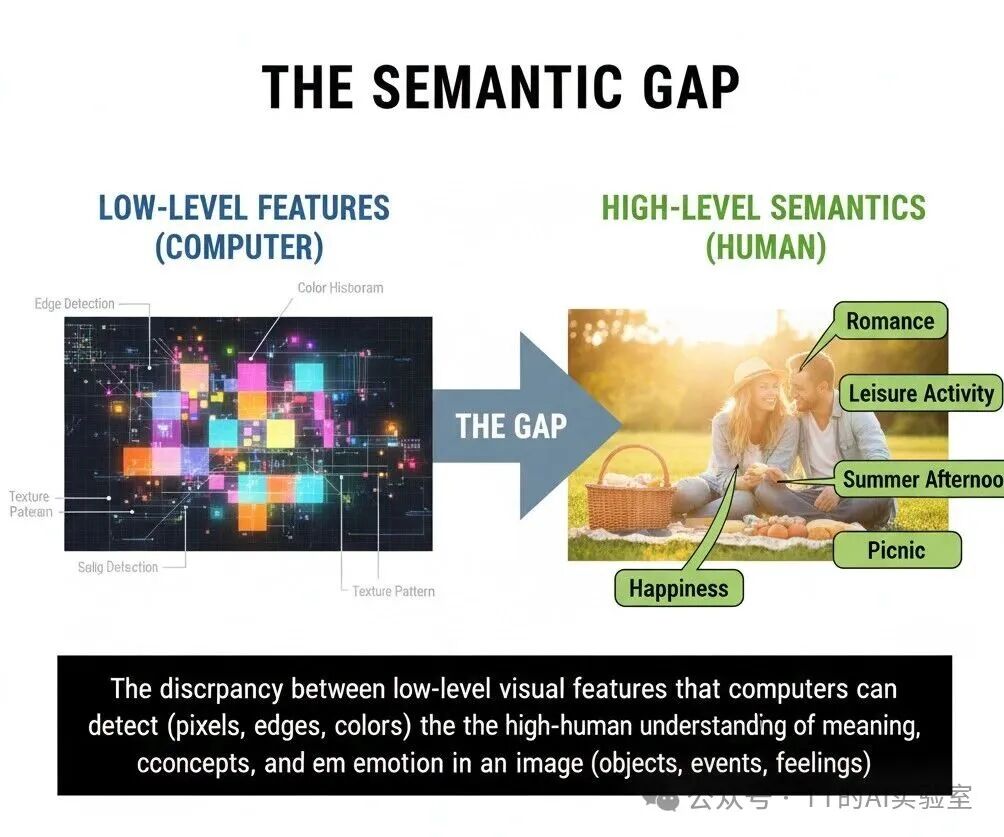
如果把分类比作解答复杂数学大题,隐藏层就是不可或缺的中间推导步骤:
- 底层隐藏层:识别“基础笔画”。将杂乱像素关联起来,提取边缘、线条或特定方向的色块等局部特征。
- 中层隐藏层:识别“功能组件”。将底层特征原子进行组合,形成几何部件,如三角形耳朵、圆形轮子、带纹理的眼睛。
- 深层隐藏层:识别“整体概念”。通过对组件的并发检测与空间关系建模,在模型内部重构出“猫”或“汽车”的完整语境。
没有这些中间步骤,模型很难跨越从“杂乱像素”到“分类语义”之间的鸿沟。层级化(Hierarchical)的表征必不可少;缺少它,模型会退化为只能识别特定像素排列的“复读机”,抽象能力会明显下降。
三、非线性的必要性与激活函数
在神经网络的数学表达中,隐藏层的结果必须经过一个非线性变换。以最常见的两层神经网络为例:
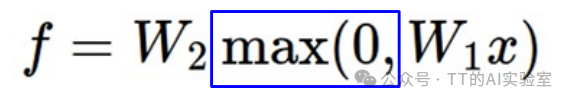
这里的 max(0,z)就是 ReLU(Rectified Linear Unit)激活函数(activation Function)。
为什么必须有激活函数?
如果没有这个非线性算子,无论堆叠多少层隐藏层,根据矩阵乘法的结合律,多个线性变换合并后依然只是一个线性变换。模型会退化回那把只能“一刀切”的直尺,深度也就失去了意义。
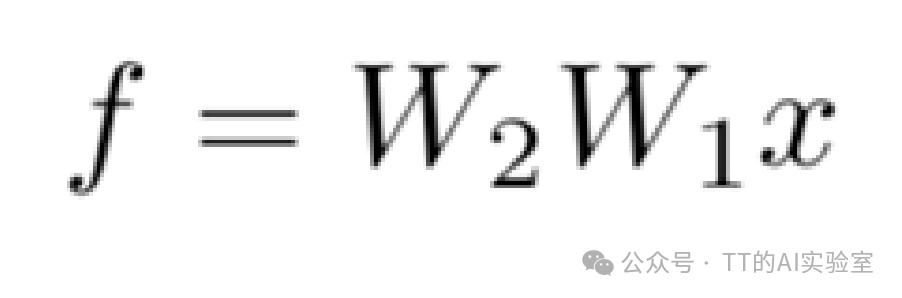
那么,常见的激活函数有哪些?
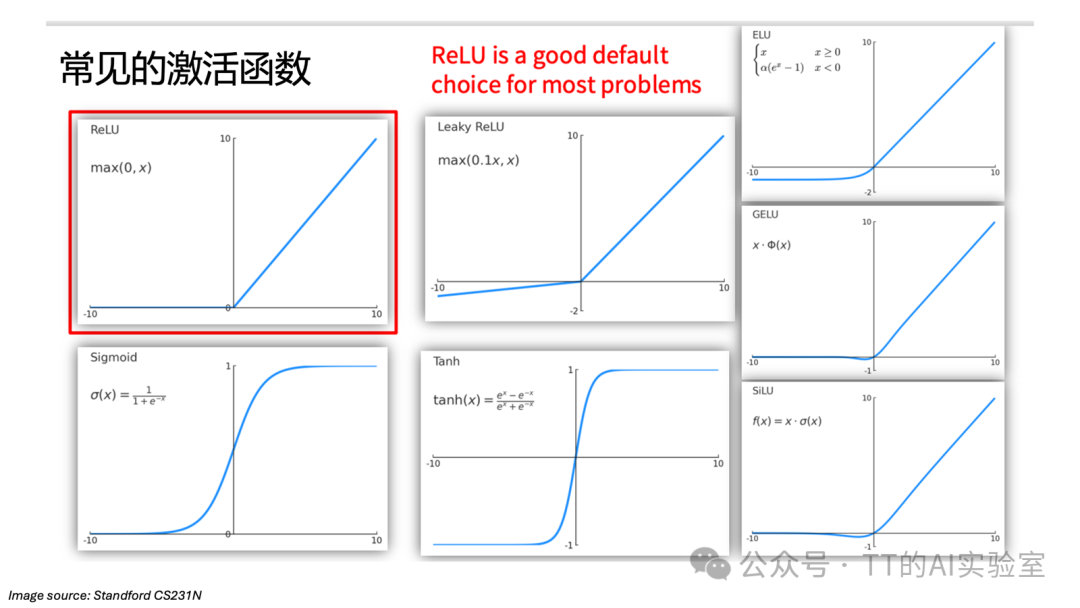
1)ReLU(Rectified Linear Unit)
- 特点:现代深层网络的默认首选。
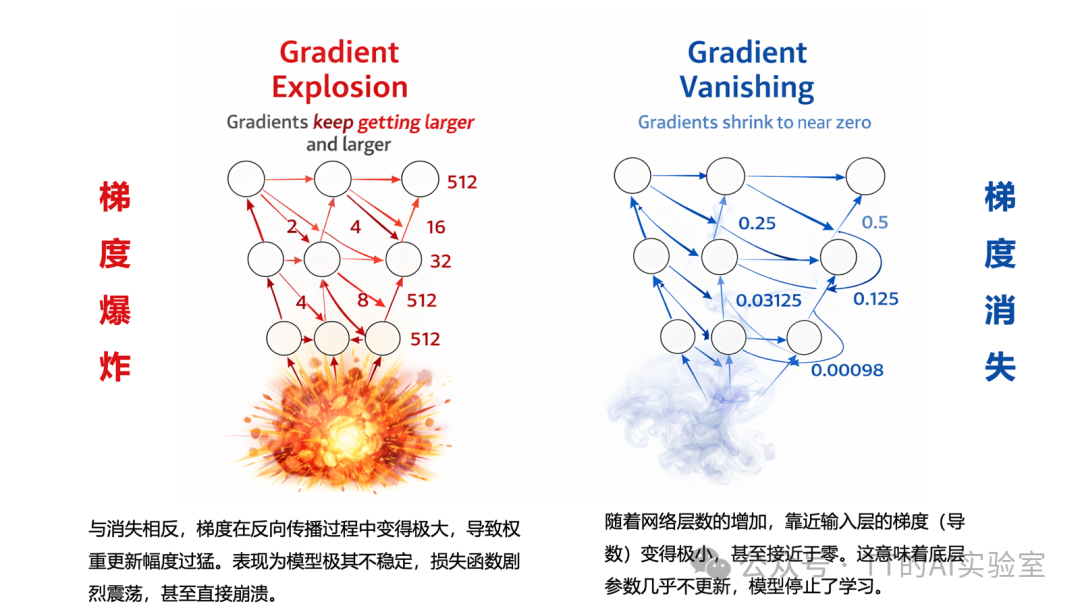
- 优劣:计算极快,有效缓解梯度消失(Gradient Vanishing)问题;但可能导致“死亡神经元”(输入为负时梯度永久归零)。
- 应用:广泛应用于各种 CNN 隐藏层。
ReLU 的变体:
2)Leaky ReLU
- 特点:针对 ReLU 缺陷的改进方案。
- 优劣:给负区间一个小斜率,确保梯度在输入为负时依然能流动,解决神经元死亡问题。
- 应用:当训练过程中出现大量 ReLU 失活时使用。
3)ELU(Exponential Linear Unit)
- 特点:相比 ReLU,负区间过渡更平滑。
- 优劣:输出均值更接近零,有助于加速收敛;但涉及指数运算,计算成本略高。
- 应用:追求更高训练稳定性的深层网络。
4)GELU(Gaussian Error Linear Unit)
- 特点:引入了随机正则化的思想。
- 优劣:性能上限极高,是当前先进模型的标配。
- 应用:Transformer、BERT 及大语言模型的核心。
5)SiLU(Swish)
- 特点:曲线非常平滑且非单调。
- 优劣:在深层网络中表现优于 ReLU。
- 应用:常见于 EfficientNet 等追求能效比的视觉架构。
6)Sigmoid
- 特点:将输出压缩至 (0,1)。
- 优劣:极易导致梯度消失,且输出非零中心化。
- 应用:主要用于二分类任务的输出层。
7)Tanh(双曲正切)
- 特点:将输出压缩至 (−1,1)。
- 优劣:输出零中心化(比 Sigmoid 更好收敛),但依然存在梯度消失风险。
- 应用:常用于循环神经网络(RNN)或对对称性有要求的层。

在工程实践中,激活函数的选择往往遵循一个简单原则:性能优先,效率兼顾。常用策略如下:
1)快速验证、简单网络 → ReLU
ReLU 凭借分段线性(Piecewise Linear)的特性,既计算高效,又能缓解深层网络的梯度消失问题。它几乎成为现代深度学习的“工业标准”,适合建立实验基准(Baseline),验证模型学习能力。
2)大模型、复杂语义 → GELU
在大规模模型,尤其是 Transformer 或大语言模型(LLM)中,GELU(Gaussian Error Linear Unit)逐渐成为优选。它通过高斯误差函数对激活进行平滑加权,提供更精细的非线性表征能力,同时带来更稳健的收敛效果。
3)输出层概率映射 → Sigmoid(隐藏层慎用)
除非用于二分类任务的输出层做概率映射,否则隐藏层几乎不使用 Sigmoid。原因很直接:Sigmoid 在输入远离零点时导数接近 0,梯度消失会层层累积,底层参数得不到有效更新,训练很容易“卡住”。
四、模型容量、过拟合与正则化
在神经网络架构设计中,一个核心挑战是:如何在表达能力与泛化稳定性之间找到更好的平衡。
1)模型容量(Capacity):定义“智力”的天花板
模型容量由参数规模决定,具体表现为网络宽度与深度的组合:
- 深度(Depth / 层数 Layers):逻辑推导的阶数。决定模型能进行多少次连续的非线性变换。层数越深,从原始像素到高级语义的“抽象跨度”通常越稳健。
- 宽度(Width / 神经元数 Neurons):并行特征捕获量。决定模型在同一层级能同时建模多少种不同的视觉模板(templates)。
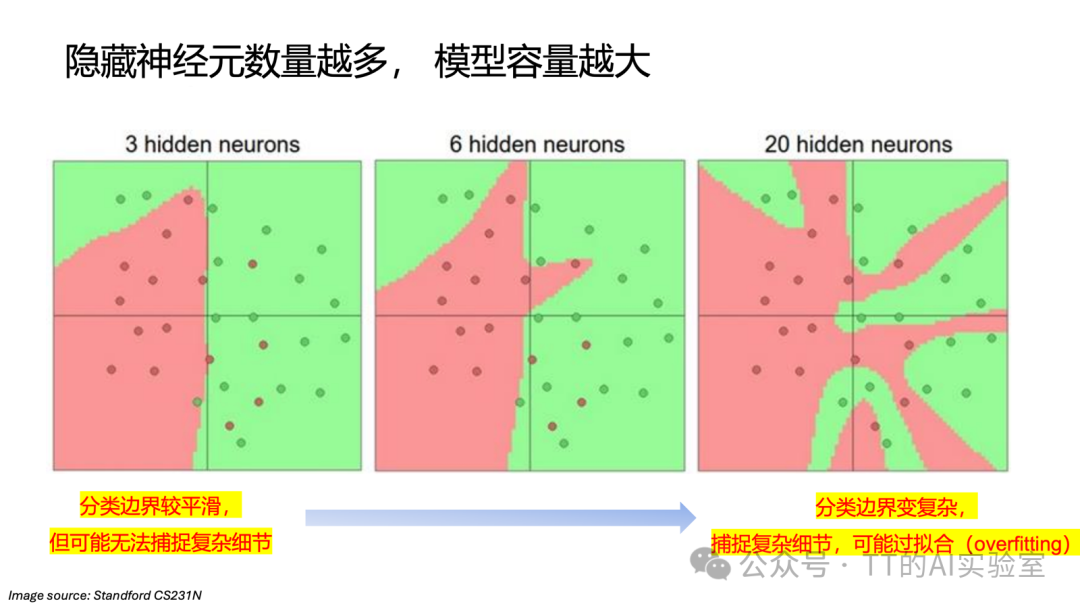
从图中可以看到:神经元数量增加 → 表达能力增强 → 模型容量扩大 → 过拟合(Overfitting)风险上升。
但在实际工程里,共识并不是通过缩小网络(降低“智力”)来防止过拟合,而是构建容量充足的网络,并引入正则化(Regularization)来约束它。
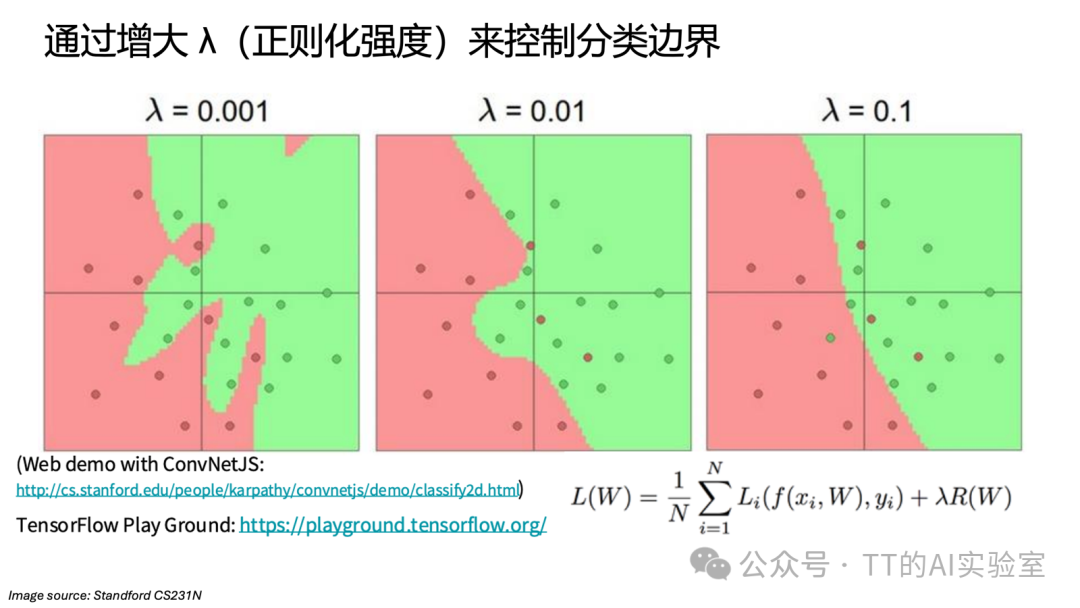
2)正则化强度 λ:模型复杂度与泛化性能的杠杆
以 L2 正则化(权重衰减)为例,它在损失函数中增加了对权重大小的惩罚项。本质上是预测误差与模型复杂度之间的杠杆:
- 过大:约束过强。为了让权重尽量小,模型不得不放弃复杂推导,边界变得过于平滑甚至趋于直线,模型变“木讷”,出现欠拟合(Underfitting)。
- 适中:理想状态。模型在准确拟合数据与保持边界简洁之间达成平衡,边界仍具备非线性灵活性,但过滤掉随机噪声干扰,泛化能力更好。
- 过小:缺乏约束。模型过度关注训练噪声,分类边界异常复杂,为了迁就离群点不断扭曲边界,出现过拟合(Overfitting)。
补充:关于正则化更多内容,可回顾过往推文《计算机视觉基础 03|正则化 Regularization》。
五、生物神经元的启发
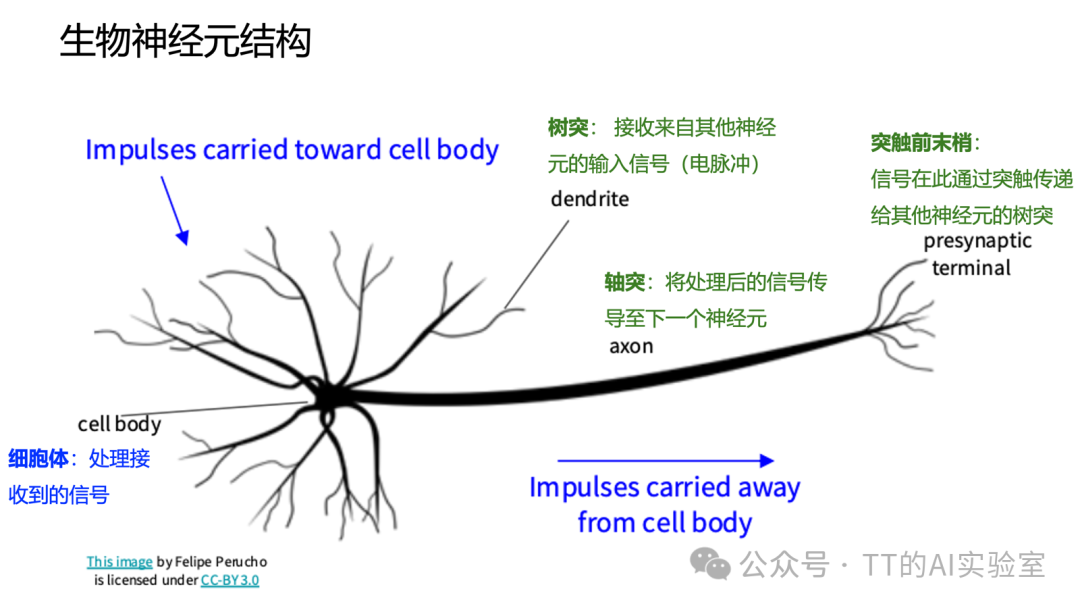
人工神经网络的灵感来自生物神经元。先回顾一下:在生物系统中,一个神经元主要做三件事:
- 接收信号:树突(dendrite)来自其他神经元的电信号输入
- 处理信号:细胞体(cell body)接受并处理来自不同来源的信号
- 传递信号:当整体刺激超过阈值,轴突(axon)才会“激活”,将处理后的信号传导至下一个神经元
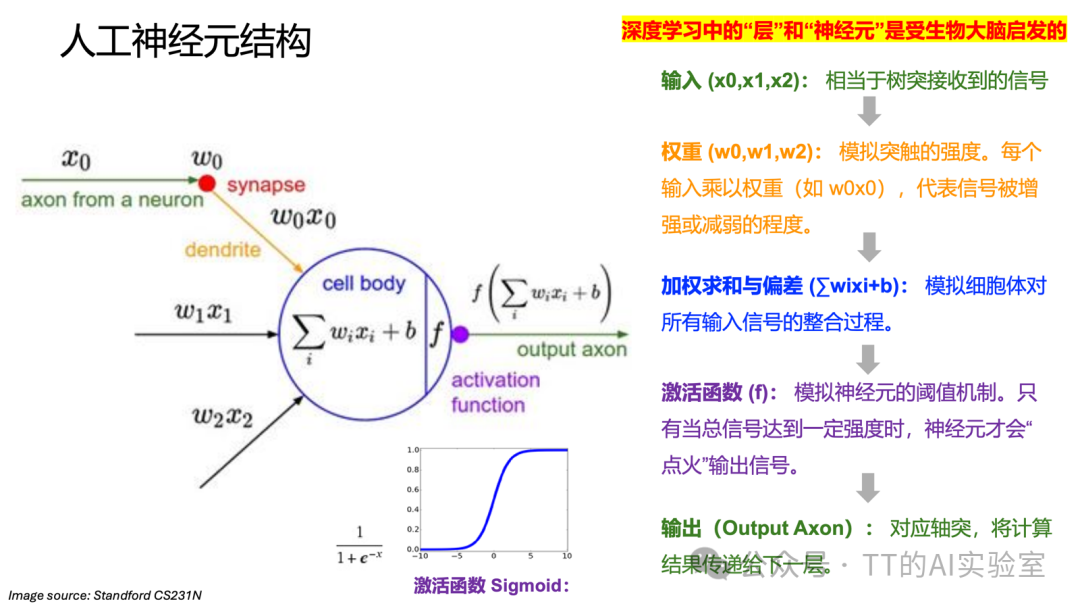
因此人工神经元通常会进行粗略类比:
- 树突 → 输入 Input
- 细胞体 → 加权求和 + 激活函数
- 轴突 → 输出 Output
但需要强调:这种类比是极度简化的工程抽象。
因为真实大脑中:
- 生物神经元类型高度多样
- 树突与突触本身就具备复杂的非线性与时间动态
- 单个神经元的计算能力远超“加权求和”这一描述
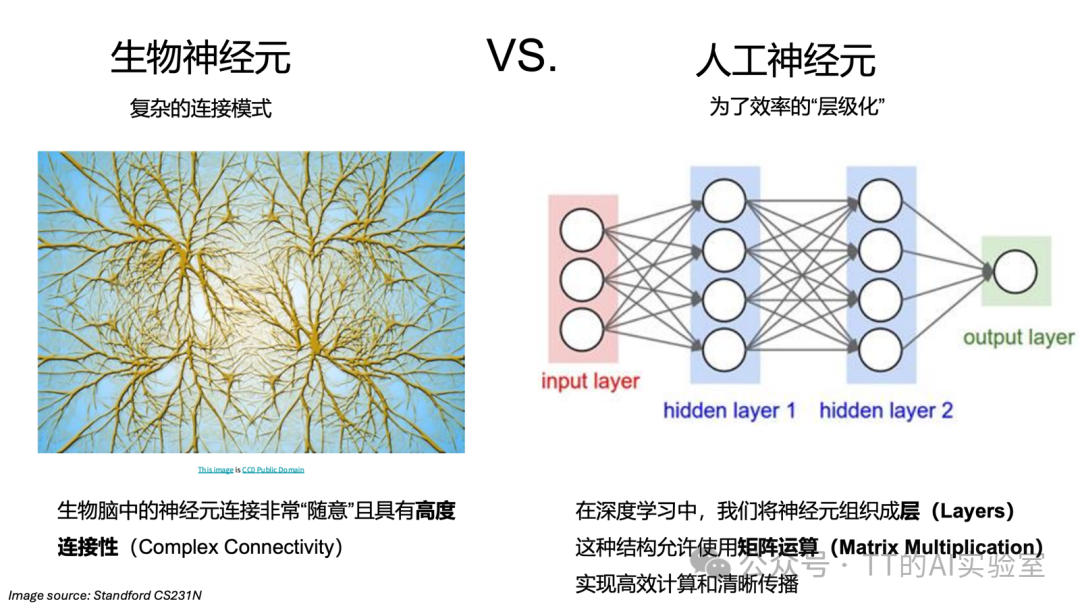
在人工神经网络中,我们主动放弃这些复杂性,把神经元压缩成统一、可微、易并行的计算单元,目的只有一个:服务计算效率与可训练性。
可见,神经网络不是大脑的数字克隆,而是受大脑启发的高效计算模型。
六、计算图与反向传播
当神经网络从几层演进到数十层甚至上百层(如 ResNet 或 Transformer)时,会遇到一个核心工程挑战:如何高效计算梯度?
这里推荐在 人工智能 相关板块继续延伸学习,很多实践问题(训练稳定性、梯度问题、架构选择)在真实工程场景里更容易“对上号”。
1)为什么不再手动推导?
模型只有一两层时,也许还能在纸上推导导数公式 ∇WL。

但模型一旦复杂,手动求导会遇到几个致命问题:
- 过程冗长:涉及大量矩阵微积分,推导费时且极易出错。
- 缺乏灵活性:例如把损失函数从 Hinge Loss 换成 Softmax,或调整模型结构,所有推导都要重来。
- 不可扩展:现代深层模型下,手动推导在工程实践上不可行。
2)计算图:将复杂公式拆解
为了解决这个问题,我们引入计算图(Computational Graph)。它将复杂的嵌套公式拆解为一系列简单的基础运算节点:
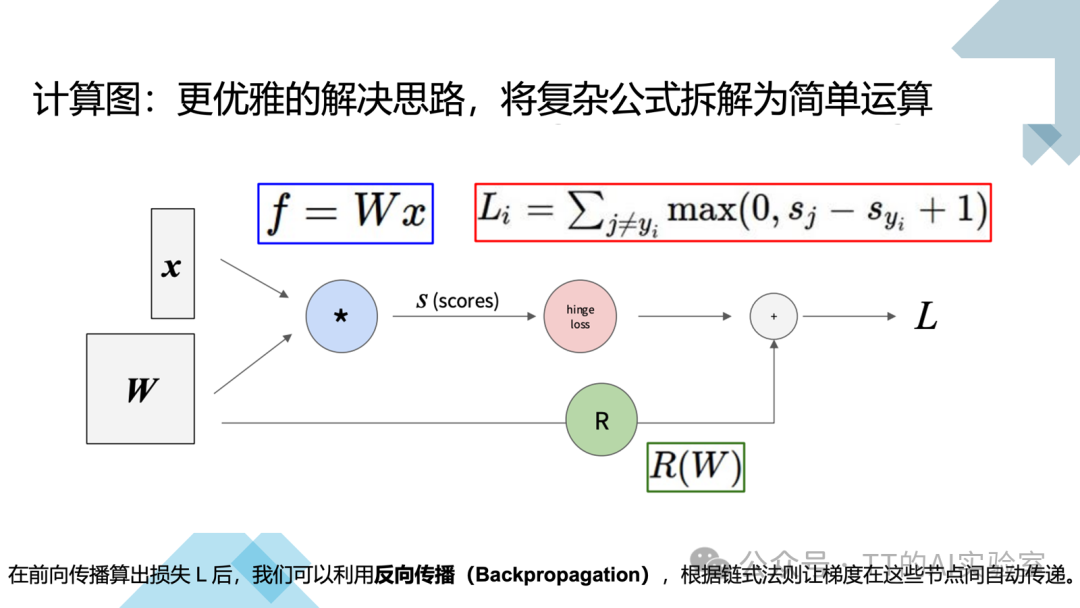
- 前向传播(Forward Pass):数据按顺序流经每一个简单运算(如乘法、加法、Hinge Loss、正则化项 R(W)),最终计算出总损失 L。
- 反向传播(Backpropagation):计算图的灵魂。基于链式法则(Chain Rule),梯度沿计算图反向回溯,自动计算每个权重(如 W1、W2)对最终误差的贡献。
计算图的出现,让我们可以像“搭积木”一样自由组合复杂模型架构。开发者只需要定义好前向传播逻辑,而繁琐的求导工作则交给自动求导框架完成。
本篇小结
神经网络并非不可理解的“黑盒”,它本质上是特征的线性加权与非线性激活层层嵌套的结果:
- 层级结构:通过权重的多层叠加,赋予模型由表及里、从局部到全局的特征抽象能力。
- 非线性激活:打破线性运算的局限,使模型能够拟合极其复杂的函数空间,处理现实中非线性分布的数据。
- 正则化:作为惩罚机制,在拟合当前数据与保持模型稳健性(泛化能力)之间起到平衡杠杆的作用。
