深度神经网络数学与物理本质：从高维几何映射到损失景观动力系统

神经网络的卓越表现常引人关注，但更值得深入探究的是其背后的数学形式与物理性质。超越将其视为简单的矩阵与非线性组合的视角，从分析结构、空间映射及动力系统等多条路径展开，能揭示其超越工程实现的深刻理论内涵。

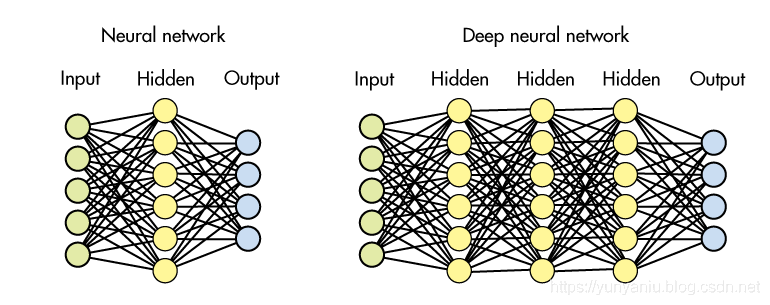
1 神经网络的数学基础：函数族、映射结构与可表达性

1.1 从函数逼近视角理解网络：可表示函数族的结构

现代神经网络的数学本质根植于函数逼近理论。一个前馈神经网络可被严格视为由参数张成的高维函数族：$f(x；\theta)$，其中 $x$ 为输入，$\theta$ 为参数。这意味着，一个神经网络不是一个固定函数，而是一个高维函数流形。

1.1.1 逐层线性变换与点状非线性的代数结构

一个深度网络的第 $l$ 层可抽象为：$h_l = \sigma(W_l h_{l-1} + b_l)$。
从线性代数看，$W_l$ 是作用于向量空间的线性算子，而 $\sigma$ 是打破线性的逐点非线性激活函数。以 ReLU 为例，网络输出可写为分段线性形式，这意味着神经网络是分段线性函数族。

分段线性函数族的数学特征包括：

• 每一段由仿射映射构成。
• 可用的线性片段数量随网络深度呈指数级增长。
• 激活函数决定了网络的“折叠复杂度”。

因此，网络的整体表达形式可写为 $f(x) = A_i x + b_i$，其中每个区域 $R_i$ 是输入空间被网络划分后的结果。

1.1.2 通用逼近定理的严格内涵与常见误解

通用逼近定理指出，只要隐含层足够宽，网络即可逼近任意连续函数。这一结论对理解表达能力至关重要，但也常被误解：

• 它并未保证训练过程能找到该逼近。
• 未说明收敛速度与参数规模的关系。
• 未涉及表达复杂度、平滑性或泛化性能。

从数学上看，这引出了更深层的问题：网络所表达的函数族是否构成某种拥有良性几何或分析结构的集合？这涉及到分段线性函数的复杂度、函数空间的VC维度等理论。

1.2 神经网络的几何解释：高维空间中的折叠与再分布

从几何视角理解神经网络是近年来的理论趋势。每一层都可视为高维空间中的几何操作：

• 线性层：对空间进行旋转、缩放、剪切。
• 非线性层：对空间进行折叠、截断，引入边界。
• 多层复合：在高维空间中形成复杂且指数级的区域分割。

1.2.1 线性变换对几何结构的影响

线性变换 $W_l$ 的几何意义包括改变特征方向的度量、强化或收缩某些方向以过滤噪声。若对其作奇异值分解，其作用可分解为旋转坐标轴、缩放不同方向，再旋转至新的基底。每一层都是一次高维空间的重新构型。

1.2.2 激活函数作为“折角制造器”

以 ReLU 为例，其几何意义是沿超平面将高维空间切开，在一侧折叠成线性区域。一个 $L$ 层 ReLU 网络能构造的分区数量满足指数级增长理论。这意味着深度网络能够制造极其复杂的区域划分，使得输入经过折叠后变得更“线性可分”。

1.2.3 神经网络的几何目标：让复杂数据变简单

网络的几何任务可以总结为：将原本复杂、非线性、纠缠的数据分布，映射为在某些坐标轴上更容易分割的形态。例如，两类复杂分布可能被“拉直”，异常点被挤压到远离正常样本的区域。这揭示了神经网络通过构造新的特征空间，使数据在该空间内呈现更简单几何结构的核心观点。

1.3 神经网络、维度扩展与隐式嵌入

深层网络在数学上类似于一种“隐式高维嵌入”机制。

1.3.1 不显式升维的升维效应

即使输出维度未提高，网络的多层结构仍能隐式构造高维表示：ReLU激活将不同区域折成不同线性片段，相当于离散化构造了许多“隐含维度”；深度叠加创建指数级增长的线性区域，整体效果类似于进入更高维空间。数学上可用雅可比矩阵秩的变化反映这一性质。

1.3.2 嵌入视角：网络作为高维展开器

从嵌入理论看，神经网络类似于从低维到高维空间的嵌入，其表达能力本质上可理解为：通过多层结构隐式构造多个“维度跳跃”，从而使数据在适合的几何空间中更易处理。

2 神经网络的物理解释：能量最小化、动力系统与统计机制

神经网络的训练与推理可以从物理体系的动力学、能量演化和统计行为角度找到严格对应。

2.1 训练过程作为“能量下降过程”：梯度流视角

训练的目标是最小化损失函数 $L(\theta)$。梯度下降法本质上是一个离散时间动力系统：$\theta_{t+1} = \theta_t - \eta \nabla L(\theta_t)$。

从物理意义看，损失函数 $L$ 可被视为势能函数：

• 参数 $\theta$ 是粒子的位置。
• 梯度 $\nabla L$ 是能量场的斜率。
• 优化过程是粒子在能量场中下滑。
• 随机梯度下降 则对应于具有噪声的动力学过程。

若学习率足够小，梯度下降可近似为连续时间微分方程：$d\theta/dt = -\nabla L(\theta)$，这与物理中的梯度流相同，描述能量自然减少的过程。

2.2 损失函数景观的能量地形结构

参数空间是高维空间。损失函数在此空间的几何性质与传统物理中的能量地形高度相似。

2.2.1 为何局部极小值多数是“好”解？

理论与实验发现：

• 在高维空间中，坏的局部极小值非常稀有。
• 大多数极小点高度相似。
• 训练更可能落在“宽阔的谷底”。

这一现象可用随机矩阵理论解释：Hessian矩阵的特征值分布使得陡峭点极少。从统计物理视角看，训练过程类似于多体系统在能量景观中寻觅低能态，大多数可达的低能态结构相似。

2.2.2 SGD的随机性等同于带温度的动力演化

随机梯度下降可写作 $\theta_{t+1} = \theta_t - \eta g_t$，其中 $g_t$ 是小批量带来的噪声。这物理上等价于有温度的分布、布朗运动，或在能量地形中的随机游走，这使其能逃离“尖锐局部极小值”，收敛到更“平滑”的低能区，从而解释了其良好的泛化性能。

2.3 神经网络作为动力系统：迭代映射与连续深度

考虑网络的层级结构 $h_{l+1} = \sigma(W_l h_l + b_l)$，这是典型的迭代动力系统形式：$h_{l+1} = F_l(h_l)$。深度越深，迭代越多。

2.3.1 连续深度极限：Neural ODE的数学基础

若层数趋于无穷但每层变化趋于无穷小，网络等价于一个常微分方程系统：$dh(t)/dt = F(h(t), \theta(t))$。
其物理意义包括：神经网络等价于“时间演化”，网络深度等于动力系统演化的时间。这构成了 神经微分方程 的理论基础。

2.3.2 稳定性、分岔现象与动力行为

动力系统理论可用于解释网络行为：

• 梯度发散/消失对应于不稳定动力系统。
• 网络可能形成吸引子。
• 梯度传播由雅可比矩阵的谱半径控制。

2.4 神经网络与统计物理：大规模参数系统的平均场理论

现代神经网络参数规模巨大，可自然应用统计物理中的多体分析方法。

2.4.1 平均场理论

以无限宽网络为例，当宽度 $n \to \infty$ 时，网络输出趋于高斯过程。其行为类似于物理中的平均场系统，个体参数的影响被整体统计分布等效取代。

2.4.2 能量景观与玻璃态物理的类比

深度网络的损失景观与自旋玻璃模型高度类似：有大量近等价低能态、能量呈多谷结构、噪声使系统在形态间跳跃。这与玻璃态物理有极强对应性。

3 神经网络的高维几何意义：曲率、分区与特征流形

3.1 激活函数对空间曲率的影响

以 ReLU 为例，它会将空间沿超平面截成分段区域。一个 $L$ 层网络能构造指数级数量的分区，其几何意义可理解为不断细化输入空间的工具。

3.2 表示学习中的特征流形

数据通常集中在某个低维流形附近。神经网络通过多层结构逐渐将这个流形映射到更易处理的形态，例如将高维图像流形展开、平铺或对齐，此即“流形变换”思想。

3.3 角度、距离与度量结构的重构

神经网络通过权重矩阵与激活函数重塑输入空间的度量结构：放大某些方向，压缩另一些方向。训练的结果即是找到一种“任务适配的度量结构”。

4 神经网络的计算理论意义：复杂度与参数效率

4.1 神经网络作为可计算函数模型

在可计算性层面，神经网络等价于一种由线性算子和局部非线性构成的可计算模型，其能力可与递归函数、电路复杂度模型类比。

4.2 深度与宽度的复杂度差异

数学上可证明，在表达相同目标函数时，深度网络的参数量可能远小于浅层网络。深层结构在计算复杂度上更具优势。

4.3 参数空间的结构与高维优化

尽管参数数量庞大，但参数空间存在大量冗余（退化方向、重复结构），这使得训练更容易进入“宽阔的低点区域”。

5 神经网络在物理启发下的进一步类比

5.1 网络参数作为“场”

若将每一层权重视为定义在离散层索引上的场变量，整个网络就形成了一个分布在层维度上的场结构，训练类似于对这些场变量施加能量驱动。

5.2 分布式训练行为

采用 随机梯度下降 时，参数更新受噪声影响，在损失地形中进行近似随机分布并逐步下降，类似于物理体系的随机分布过程。

5.3 超大规模模型的统计趋势

大型网络由于宽度巨大，其行为可用平均场理论近似：输出分布趋向高斯，梯度呈现集中性质，参数波动可近似为统计过程。