二叉树遍历序列递归重构：中序+前序求后序（含美国血统）、中序+后序求前序详解

在学习了栈与队列等线性结构之后，我们常常会遇到关于二叉树遍历序列转换的经典问题。这类问题的核心，是如何利用已知的两种遍历序列，推导出第三种遍历序列。本期我们将深入探讨两种常见场景：通过中序+前序求后序，以及通过中序+后序求前序，并结合具体的OJ题目进行实战分析。

其核心原理是递归分治。无论是前序（根左右）还是后序（左右根），其第一个或最后一个节点必然是当前子树的根节点。我们可以在已知的另一种遍历序列（通常是中序）中定位到这个根节点，从而将整个序列清晰地划分为左子树和右子树区间。基于这一划分，我们便可以递归地处理左右子树，并在递归回溯时，按照目标遍历序列的顺序来拼接结果。

一、已知中序和前序，求后序遍历序列

T1. [USACO3.4] 美国血统 American Heritage

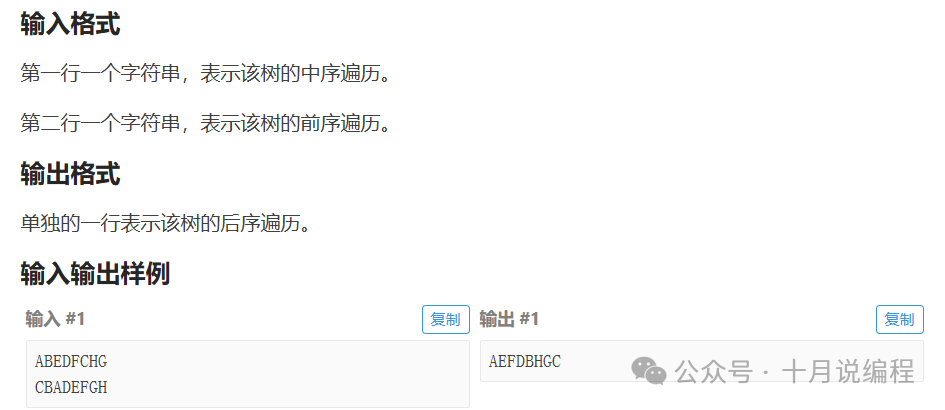
这道题是已知二叉树的中序遍历序列和前序遍历序列，要求我们输出它的后序遍历序列。

解题思路：

前序遍历的特点是“根左右”，所以序列的第一个字符一定是当前子树的根节点。我们可以利用这个根节点，去中序遍历序列中找到其位置，从而将中序序列一分为三：左子树、根、右子树。确定了左右子树的区间后，我们就可以递归地对左子树和右子树进行相同的处理。

由于目标是后序遍历“左右根”，因此在递归处理时，我们需要先递归处理左子树，再递归处理右子树，最后在回溯时，将当前根节点拼接到结果字符串的末尾。

参考代码实现：

#include<bits/stdc++.h>
using namespace std;
queue<char> q;//存储前序序列
char mid[30];//存储中序序列
string s1,s2,ans;
int n,l,r;
void dfs(int l,int r){
    if(l>r) return ;//递归出口，区间无效
    char root=q.front();//前序队列队首即为当前根节点
    q.pop();//出队
    for(int i=l;i<=r;i++){
        if(mid[i]==root){//在中序序列中找到根节点位置
            dfs(l,i-1);//递归处理左子树
            dfs(i+1,r);//递归处理右子树
            ans+=root;//回溯时拼接，形成后序序列
            break;
        }
    }
}
int main(){
    cin>>s1>>s2;//输入中序(s1)和前序(s2)
    int n=s1.size();
    for(int i=0;i<n;i++) mid[i]=s1[i];//中序存入数组
    for(int i=0;i<n;i++) q.push(s2[i]);//前序存入队列
    dfs(0,n-1);//从整个序列区间开始递归
    cout<<ans;
    return 0;
}

在这段代码中，我们使用队列来管理前序序列，按序取出根节点。递归函数 dfs 是整个DFS（深度优先搜索）过程的核心，它不断地划分区间并确定子树的根。

二、已知中序和后序，求前序遍历序列

T2. [NOIP2001普及组] 求先序排列

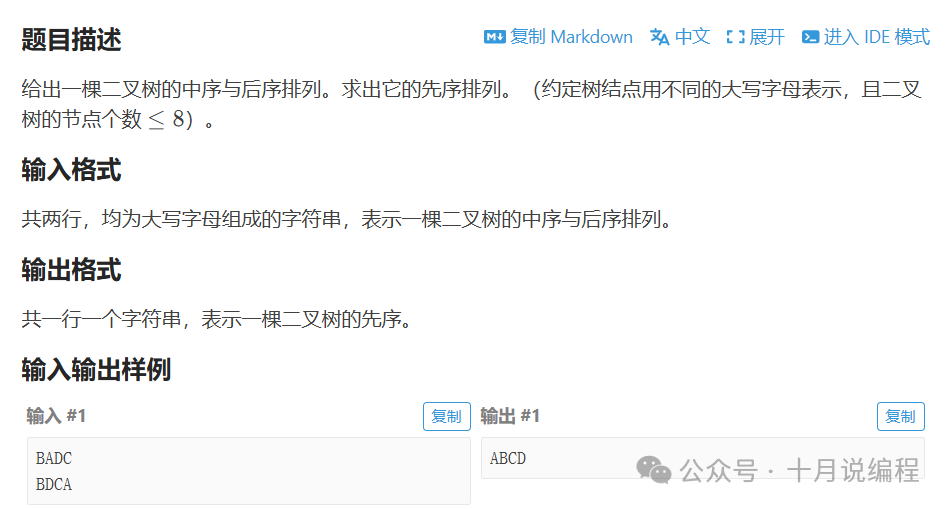
这道题是已知二叉树的中序遍历序列和后序遍历序列，要求我们输出它的前序遍历序列。

解题思路：

后序遍历的特点是“左右根”，所以序列的最后一个字符是当前子树的根节点。但为了处理方便，我们可以先将后序序列反转。反转后，序列的顺序就变成了“根右左”。这时，我们就可以像处理前序序列一样，从序列头部依次取出根节点。

同样地，用这个根节点去分割中序序列。由于反转后序序列的处理顺序是“根右左”，所以在递归时，我们需要先递归处理右子树，再递归处理左子树。在回溯时，因为我们要得到前序序列“根左右”，所以需要将当前根节点拼接到结果字符串的头部。

参考代码实现：

#include<bits/stdc++.h>
using namespace std;
queue<char> q;//存储反转后的后序序列
char mid[30];//存储中序序列
string s1,s2,ans;
int n,l,r;
void dfs(int l,int r){
    if(l>r) return ;//递归出口
    char root=q.front();//反转后序列的队首即为当前根节点
    q.pop();
    for(int i=l;i<=r;i++){
        if(mid[i]==root){//在中序序列中找到根节点位置
            dfs(i+1,r);//先递归处理右子树
            dfs(l,i-1);//再递归处理左子树
            ans=root+ans;//回溯时将根节点拼接到结果前面，形成前序序列
            break;
        }
    }
}
int main(){
    cin>>s1>>s2;//输入中序(s1)和后序(s2)
    int n=s1.size();
    for(int i=0;i<n;i++) mid[i]=s1[i];
    //关键步骤：将后序序列反转后入队，使其处理顺序变为“根右左”
    for(int i=0;i<n;i++) q.push(s2[n-1-i]);
    dfs(0,n-1);
    cout<<ans;
    return 0;
}

这段代码巧妙地运用了队列来模拟反转后的后序序列访问顺序。通过调整递归子树的顺序（先右后左）和结果拼接的位置（前插），我们高效地得到了前序遍历序列。

总结与拓展

通过以上两个例题，我们掌握了基于中序遍历序列，配合另一种序列来重构二叉树遍历结果的核心方法。关键在于：

1. 确定根节点：从前序（首位）或后序（末位/反转后首位）获取。
2. 分割中序序列：用根节点将中序序列划分为左右子树区间。
3. 确定递归顺序：根据目标序列（后序或前序）调整处理左右子树的先后顺序。
4. 确定拼接时机与位置：在递归回溯时，按照目标序列的规则（前序：根左右；后序：左右根）拼接节点。

这个递归分治的思想是解决许多二叉树相关问题的基础。希望本文的解析能帮助你彻底理解这一过程。如果你在练习其他二叉树题目时遇到问题，欢迎来云栈社区交流讨论，这里有很多热爱算法的开发者一起切磋成长。