优惠券组合优化难题：用回溯算法在200ms内求解最高性能工程实现

有个朋友去面试京东零售的交易链路部门，应聘T7架构岗，面试官直接抛出了一个极其业务化但又充满挑战的算法问题。

面试官提问：“假设用户购物车里放了50件商品，账户里同时有100张各种各样的优惠券，比如满减、折扣、跨店、品类券等等。经过初步的可用性筛选，我们仍然有20张券属于‘可用但彼此关系复杂’的状态。现在的问题是：你如何在200毫秒内，计算出使用这20张券的最佳组合，使得用户的最终支付金额降到最低？”

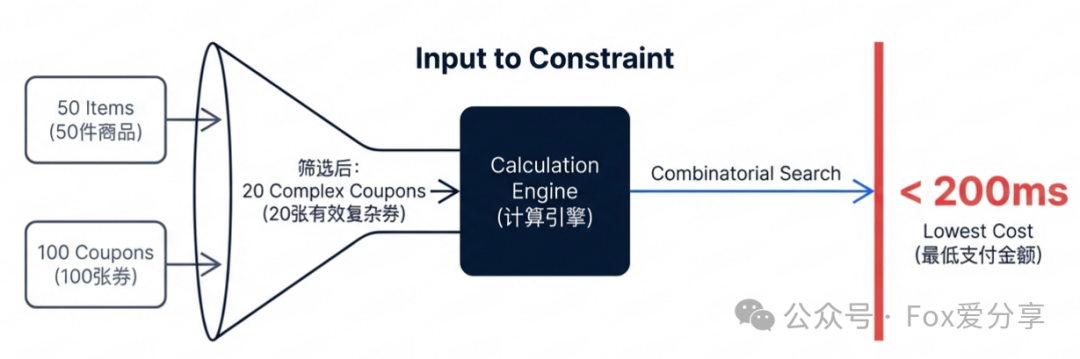
面试官紧接着追问：“为什么不用动态规划（DP）？你的代码里又该怎么避免GC问题？”

如果你只回答用“回溯法”，面试官可能只会给你及格分。但如果你能清晰阐述为何DP不适用，并给出工程级的优化方案，那才是他们想看到的。接下来，我们就来拆解这套融合了算法辩证、图论降维与内存级优化的工业级解决方案。

一、 灵魂拷问：为什么不能直接上动态规划？

这是面试中检验你算法深度与业务理解的关键点。标准的“凑单”或“背包”问题，教科书式的答案往往是动态规划。如果你直接说用回溯，会显得功力尚浅；但如果你能有理有据地解释为什么DP在这里行不通，那你展示的就是解决实际业务问题的专家思维。

1. DP的局限性在何处？

动态规划的核心在于状态转移方程，即 dp[i][v]。

在一个简单的01背包问题中，状态通常只有“当前物品索引”和“背包剩余容量”两个维度。然而，在真实的电商优惠券场景下，业务规则导致了“状态”的爆炸式增长：

• 互斥状态：使用了A券就不能同时使用B券。
• 门槛状态：商品X的金额必须大于199元才能使用某张券。
• 叠加与归属状态：店铺券只能由该店铺的商品金额来凑门槛，平台券则可以用全平台商品金额来凑。

如果试图为所有规则建模，构造出的DP状态可能会长得吓人：
dp[券索引][当前总价][店铺A金额][店铺B金额][已用互斥组ID集合...]

这样一个高维度的DP表，其内存占用会瞬间溢出（OOM），并且代码的可读性和可维护性几乎为零。

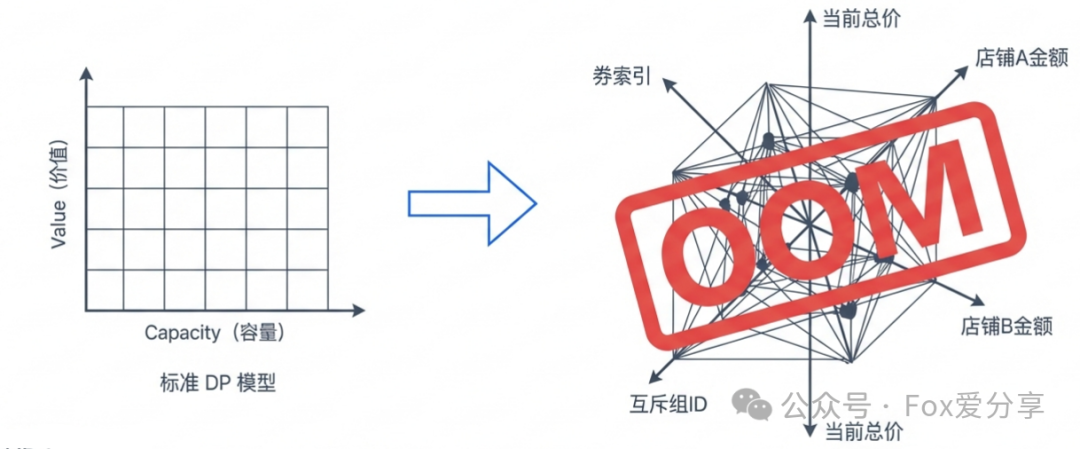
2. 架构师的结论

“在业务约束极度复杂的场景下，回溯法（Backtracking）虽然理论时间复杂度是指数级的，但配合强有力的剪枝策略，是工程实践中唯一在可维护性和性能上都能得到控制的解法。”

这个结论体现了在系统设计中权衡理论与工程现实的经典思路。

二、 核心加速：图论降维与剪枝艺术

既然选择了回溯，我们的核心任务就是通过巧妙的优化，将指数级复杂度的搜索空间压缩到可接受的范围。

1. 图论降维：寻找“连通分量”，分解问题

我们不能粗暴地把20张券混在一起进行全局组合计算。第一步是利用图论思想进行降维。

• 根据券与商品的适用关系，构建一张 “券-商品”关系图。
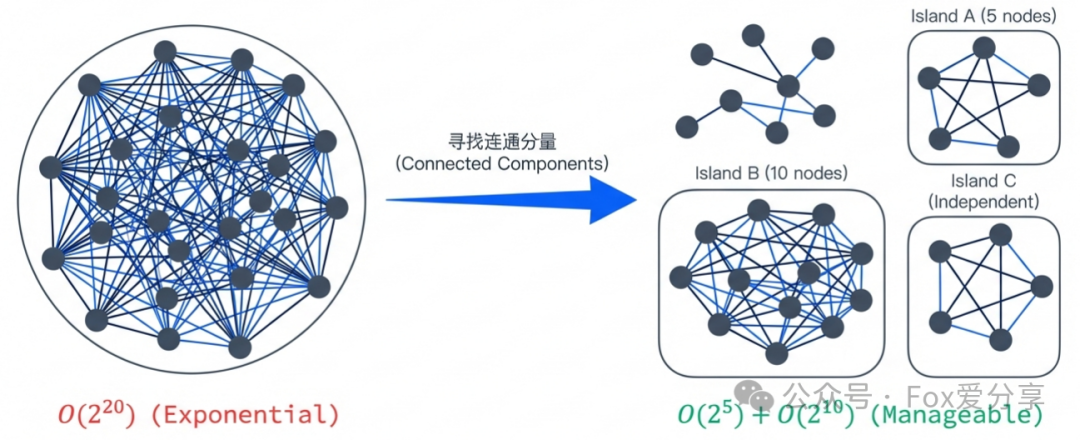
• 分析这张图，我们往往能发现，这20张券实际上可以分割成几个互不关联的 连通分量（Connected Components） ，也就是“孤岛”。
  • 例如：孤岛A（手机品类）涉及5张券和2个商品。
  • 孤岛B（零食品类）涉及10张券和20个商品。
  • 孤岛C（其他）可能只有1张独立券。

效果：这样一来，我们无需计算 O(2^20)（约100万种组合）的全局问题，而是分别计算 O(2^5) + O(2^10)（约1000种组合）的几个小问题。复杂度发生了数量级的骤降。这类问题分解的思路，在解决复杂的算法问题时非常有效。

2. 严谨的“支配剪枝”

这里必须纠正一个常见的错误思路：不能因为一张券的优惠力度小就盲目淘汰它。我们引入更严谨的 “支配（Dominance）” 关系。

定义 “券A支配券B” ，当且仅当同时满足以下三个条件：

1. 作用范围相同：都适用于同一批商品。
2. 叠加类型相同：例如都是同一店铺的满减券，且遵循相同的互斥规则。
3. 门槛更低且优惠更大：A券是“满100减20”，B券是“满100减10”。

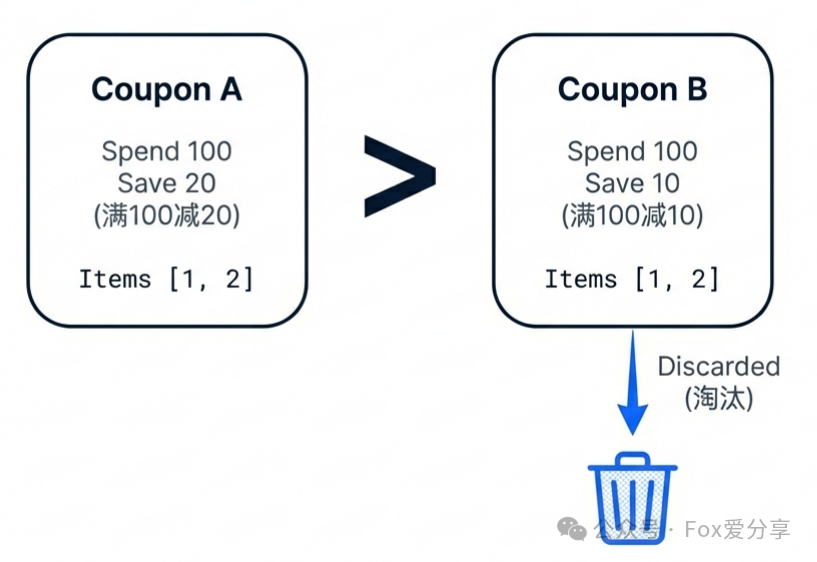
策略：只有在A严格支配B的情况下，我们才能在预处理阶段安全地丢弃B券。否则，即便B券优惠少，它也可能与其他券叠加使用，必须保留在候选集中。

3. 位图互斥剪枝：将O(N)查询优化为O(1)

这是代码实现中 usedMask 的理论基础，一个极致的优化点。

• 场景：优惠券常有“互斥组”概念（例如，同店铺的券互斥，组ID=5）。
• 传统做法：在递归函数中传递一个 Set<Integer> usedGroups。每次尝试用券前，调用 set.contains(groupId) 判断。
  • 代价：Set 是对象，涉及哈希计算、自动装箱，在百万次递归中会产生大量GC压力，性能堪忧。
• 优化解法：位运算（Bitwise Operation）。
  • 约定互斥组ID范围为0~63。
  • 使用一个 long 类型变量 mask（64位）作为位图。
  • 判断互斥：(mask & (1L << groupId)) != 0。
  • 标记使用：mask | (1L << groupId)。

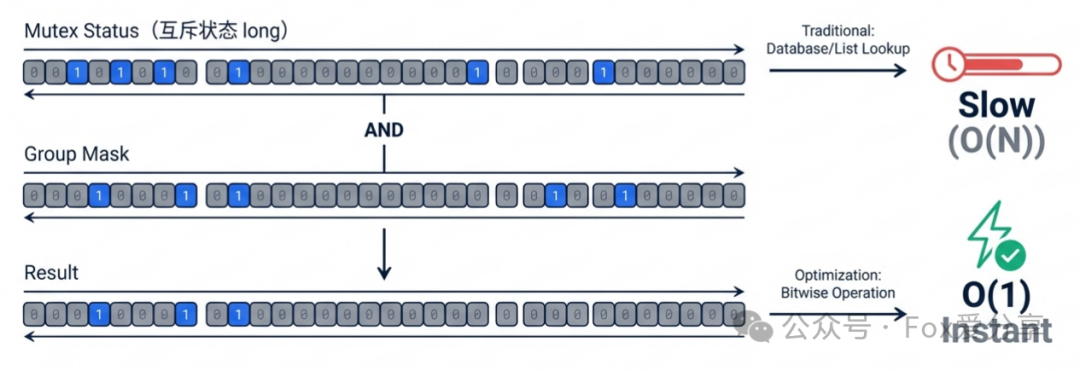
效果：将复杂的哈希集合查找变成一条CPU指令，零内存分配，速度极快。

三、 代码落地：实现“零GC”的回溯算法

为了满足200ms的苛刻要求，并防止频繁 Young GC 引发的STW停顿，我们的代码必须追求 “零对象创建” 。

• 拒绝 subList：不使用 List.subList()（它会创建新视图对象），而是传递起始索引 index。
• 拒绝 BigDecimal：全程使用 long 类型表示金额（单位为分），避免 BigDecimal 对象带来的开销。
• 拒绝 Iterator：遍历时使用 for-i 循环或直接通过索引访问 ArrayList，而非创建迭代器对象。

以下是一个高度优化的回溯核心代码示例：

public class ZeroGCCouponOptimizer {
    // 全局最优支付金额 (单位：分)
    private long minPayAmount = Long.MAX_VALUE;
    // 记录开始时间，用于超时截断
    private long startTime;

    /**
     * 对外入口
     */
    public long calculateBestPrice(List<Coupon> coupons, long originalTotalAmount) {
        this.startTime = System.currentTimeMillis();
        this.minPayAmount = originalTotalAmount; // 初始为原价

        // 1. 预处理：支配剪枝 & 排序 (金额大优先，利于快速剪枝)
        List<Coupon> optimizedCoupons = preprocess(coupons);

        // 2. 开启回溯
        backtrack(0, 0, optimizedCoupons, originalTotalAmount, 0L);

        return minPayAmount;
    }

    /**
     * 核心回溯：基于索引递归，不创建任何 List 对象
     * @param index        当前决策到第几张券
     * @param usedMask     位图：记录已使用的互斥组 ID (BitMap 优化)
     * @param coupons      券列表
     * @param currentPay   当前待支付金额
     * @param discountSum  当前已优惠总额
     */
    private void backtrack(int index, long usedMask, List<Coupon> coupons,
                           long currentPay, long discountSum) {

        // 【兜底】超时截断 (Time Boxing)
        if ((index % 100 == 0) && (System.currentTimeMillis() - startTime > 180)) {
            return;
        }

        // 【剪枝 1】最优解剪枝 (Bound Pruning)
        // 如果当前支付金额已经 >= 已知最低价，后面不用算了
        if (currentPay >= minPayAmount) {
            return;
        }

        // Base Case: 所有券都决策完了
        if (index >= coupons.size()) {
            minPayAmount = currentPay; // 更新全局最优
            return;
        }

        Coupon coupon = coupons.get(index);

        // --- 分支 A：不使用这张券 ---
        backtrack(index + 1, usedMask, coupons, currentPay, discountSum);

        // --- 分支 B：使用这张券 ---
        // 1. 门槛校验 (使用 long 比较)
        if (currentPay < coupon.getThresholdLimit()) {
            return;
        }

        // 2. 互斥校验 (BitMap O(1) 极速校验)
        long groupBit = 1L << coupon.getMutexGroupId();
        if ((usedMask & groupBit) != 0) {
            return; // 该组已经有券被使用了
        }

        // 3. 进入下一层
        backtrack(index + 1, usedMask | groupBit, coupons,
                  currentPay - coupon.getAmount(), discountSum + coupon.getAmount());
    }
}

这段代码充分体现了Java性能优化的精髓，通过控制内存分配来保障极致性能。

四、 高并发下的陷阱：如何避免“线程爆炸”？

很多候选人为求表现，会脱口而出：“把每个连通孤岛扔进 ForkJoinPool 并行计算。” 这在技术层面没错，但在高并发生产环境下，这是一个灾难性的设计。

场景还原：大促期间，系统QPS可能高达5万。如果平均每个请求需要计算3个孤岛，那么瞬间就会产生15万个计算任务去争抢有限的CPU核心。

后果：CPU将大量时间耗费在线程上下文切换（Context Switch） 上，其开销远远超过实际的计算工作，导致系统吞吐量不升反降，出现断崖式下跌。

架构师解法：自适应并行策略

我们必须根据任务的计算量级，动态决定采用串行还是并行。

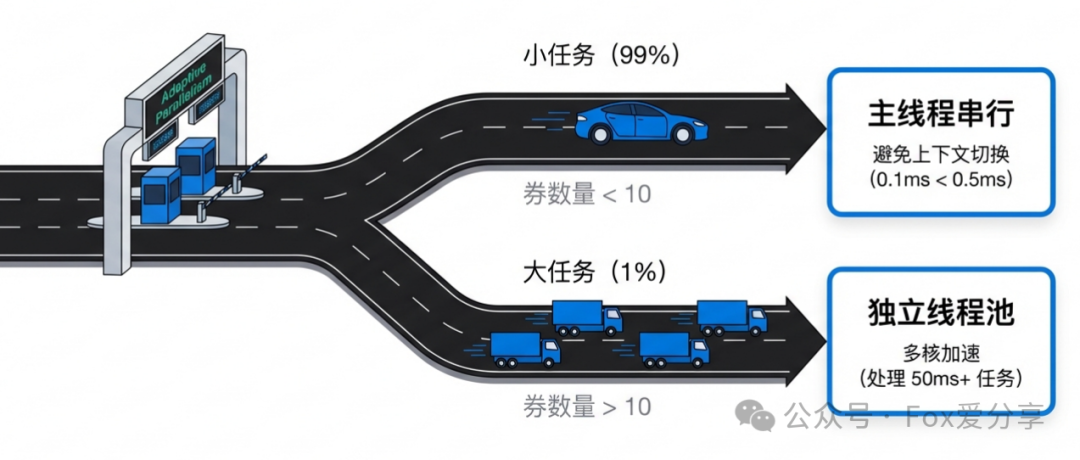
1. 小任务（占99%的场景）：
   • 如果孤岛内的券数量 < 10 张，坚决使用主线程串行计算。
   • 理由：纯CPU整数运算极快，10张券的回溯可能只需0.1ms。而启动一个线程（即使是线程池）的开销可能在0.5ms左右。此时，串行反而总体更快。
2. 大任务（占1%的场景）：
   • 如果孤岛内的券数量 > 10 张，计算量可能达到50ms+，此时将其提交到独立的、容量可控的线程池进行并行计算是值得的，可以充分利用多核优势。

核心调度逻辑：

// 自适应调度逻辑
if (island.getCouponCount() > PARALLEL_THRESHOLD) {
    // 大任务：异步并行
    completableFutures.add(CompletableFuture.supplyAsync(() -> compute(island), heavyWorkPool));
} else {
    // 小任务：当前线程直接算 (Zero Context Switch)
    results.add(compute(island));
}

五、 与规则引擎的协作：阶段分离

规则引擎（如LiteFlow、Drools） 主要用于处理灵活多变的业务规则，但其本质是解释执行或基于反射的调用，性能开销较大。绝对不能在核心回溯的递归循环内（可能执行数十万次）去调用规则引擎，否则性能必然崩溃。

架构师解法：计算阶段分离

将整个计算流程清晰拆分为两个阶段：

1. 预处理阶段（规则引擎阶段）：
   • 调用规则引擎。
   • 任务：完成券的基本可用性判断（是否过期、品类是否匹配、基础门槛是否满足）。
   • 产出：一个“纯净的”、参数化的” 券列表。将复杂的业务规则（例如“仅限Plus会员且购买生鲜商品”）转化为简单的数值型参数（如 threshold=20000, mutexGroupId=5）。
2. 核心计算阶段（回溯阶段）：
   • 严禁调用任何规则引擎或复杂业务逻辑。
   • 任务：仅进行快速的 long 类型数值比较、加减运算以及位图（BitMap）操作。

总结：规则引擎只负责 “进门安检” ，确保进入计算核心的都是“合格人员”；而核心计算则全是 “硬核的数学与位运算” ，保证速度。

六、 面试回答框架（建议融会贯通）

当再次面对“购物车最优优惠计算”这类问题时，你可以按照以下逻辑组织答案，展现全面而深入的思考。这套话术融合了算法辩证、图论降维、内存优化和高并发设计。

“面试官，这是一个典型的带有复杂约束的组合优化问题，在200ms的硬性限制下，我倾向于采用‘图论降维 + 启发式剪枝 + 零GC工程化’的综合方案：”

“1. 算法选型辩证：”
我没有选择动态规划，因为在存在多维互斥、复杂叠加和门槛规则的实际业务场景下，DP的状态空间会指数级爆炸，导致内存不可控且代码无法维护。我选择回溯法配合多层级强力剪枝，这是在业务复杂度和实时计算性能之间能找到的最佳工程平衡点。

“2. 核心降维（图论连通分量）：”
首先，我会构建 ‘券-商品’关系图，将全量券拆解为多个独立的连通分量（孤岛）。这能将一个庞大的指数级问题 O(2^n) 分解为多个可管理的小问题 O(2^n1) + O(2^n2)...，实现计算复杂度的数量级降低。

“3. 极致剪枝策略：”

• 支配剪枝：预处理阶段，严格淘汰那些被同组其他券在门槛和优惠额上完全“支配”的劣质券。
• 位图剪枝：利用 long 类型的位运算，在O(1)时间内完成互斥组校验，替代传统的HashSet，性能极高且无GC。
• 最优解剪枝：在搜索过程中，一旦当前累计支付金额超过已知最优解，立即终止该路径的搜索。

“4. S级工程优化（亮点）：”

• 零GC设计：全程使用 long（单位分）运算，避免 BigDecimal；使用索引代替 subList 和 Iterator，杜绝在递归循环中创建对象，防止Young GC引发的STW影响响应时间。
• 自适应并行：不盲目使用多线程。仅对计算量超过阈值的大孤岛启用独立线程池计算，避免高QPS下的“线程爆炸”和过高的上下文切换开销。
• 超时截断：在回溯过程中设置检查点，严格进行时间预算管理，优先保证接口的可用性和及时返回。

---

写在最后

为什么这样一道看似“凑单”的题目，能用来考察年薪50W+的候选人？

因为它考验的绝不仅仅是编写算法代码的能力。它考察的是：你是否因为深刻理解底层原理（JVM内存管理、CPU执行效率），才知道如何写出在高并发下依然稳定的代码；你是否因为透彻理解业务规则（券的互斥、叠加、门槛），才知道如何将抽象的数学模型精准落地到复杂的业务系统中。

能够把“凑单”算得准，是为用户创造价值，提升满意度和转化率；能够把“凑单”算得快，是为公司节约成本，保障系统在大流量下的稳定。这正是一名资深技术专家或架构师的核心价值所在。

希望这篇来自真实面试场景剖析的深度干货，能为你带来启发。欢迎在云栈社区继续交流更多系统设计与性能优化的实战经验。