云栈社区»论坛 › 技术文档「 Note & Doc 」 › AES算法逆向分析实战：从密钥扩展识别到加密流程还原 ...

发回帖发新帖

428 积分	0 好友	62 主题

发消息

AES算法逆向分析实战：从密钥扩展识别到加密流程还原

发表于昨天 02:53 | 查看: 7| 回复: 0

AES是一种应用广泛的对称加密算法，在软件安全与逆向分析中经常遇到。虽然其原理已有许多优秀文章阐述，但从原理映射到具体代码实现时，常常会遇到理解障碍。本文将以一个经典的C语言开源实现（tiny-AES-c）为例，结合代码深入解析AES-128的算法流程，并探讨在逆向工程中快速识别AES算法的关键特征。

密钥扩展

以AES-128为例（下文简称AES），其初始密钥长度为16字节。在加密前，明文也需要被分割为16字节的块进行处理（如ECB模式）。

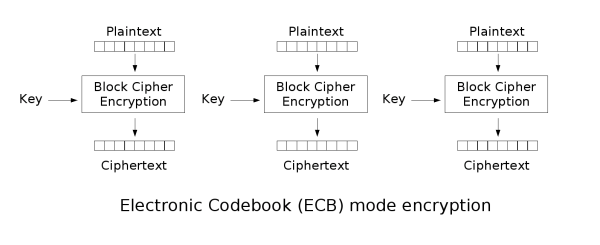
AES分组加密示意图

AES加密共进行10轮迭代，因此总共需要11个子密钥（1个初始密钥 + 10轮密钥）。利用输入的初始密钥生成后续10个子密钥的过程，称为密钥扩展。如下图所示，k0-k3为初始密钥（每块4字节），k4-k44则通过密钥扩展算法计算得出。

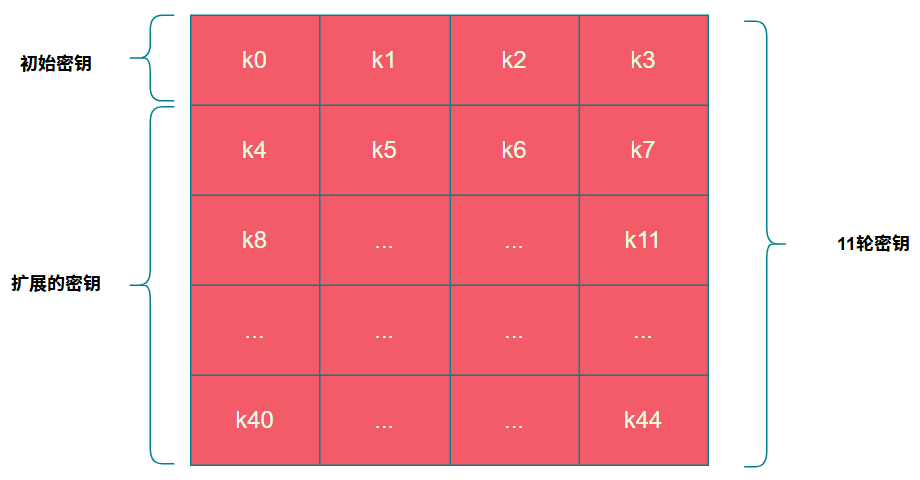
密钥扩展示意图

扩展密钥遵循公式 k[i] = k[i-4] ^ k[i-1]。但其中 k4, k8, k12...k40 等位置（即每4个一组中的第一个）的计算较为特殊，需要先对前一个密钥块 k[i-1] 进行 G函数 运算，然后再与 k[i-4] 异或。

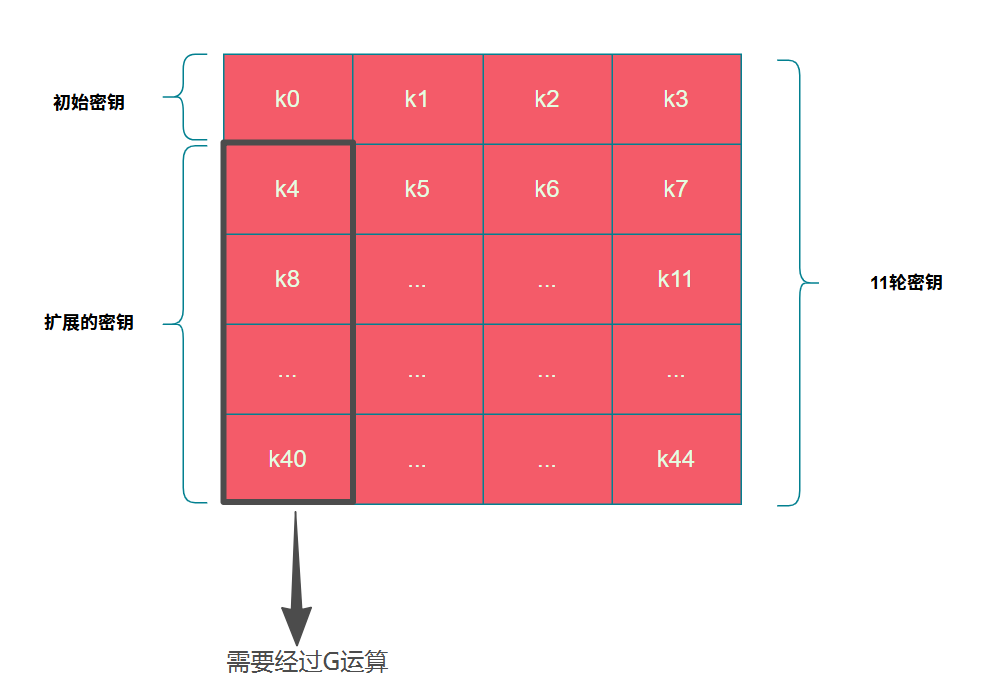
特殊位置密钥扩展公式

G运算详解

G运算包含三个步骤：行位移、S盒替换、与轮常数异或。假设 k3 = 0x11223344。

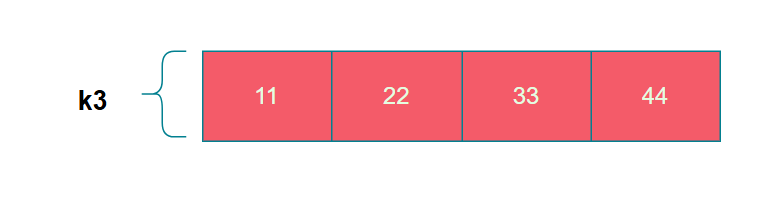
G运算流程总览

1. 行位移 (RotWord)

行位移实质是对一个4字节的密钥块进行循环左移一个字节的操作。

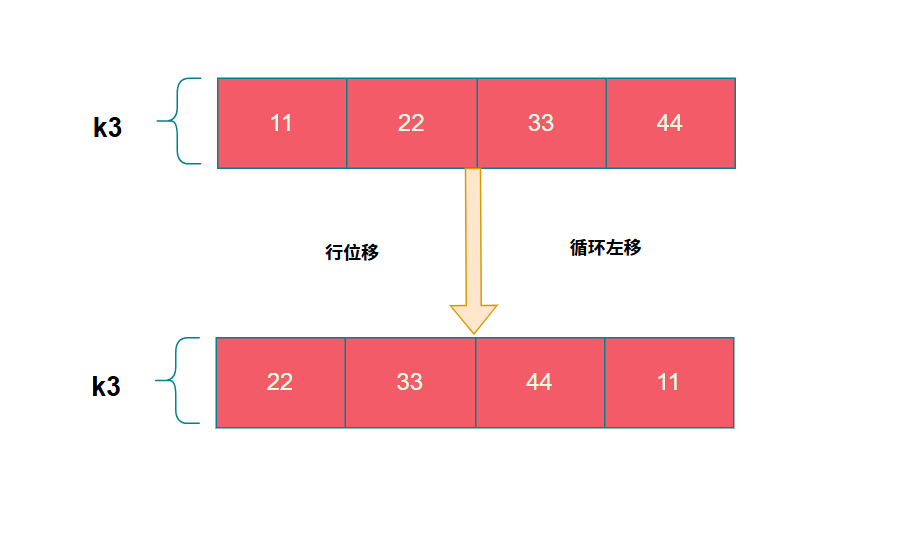
行位移操作

在tiny-AES-c中，行位移通过简单的字节交换实现：

// 行位移
const uint8_t u8tmp = tempa[0];
tempa[0] = tempa[1];
tempa[1] = tempa[2];
tempa[2] = tempa[3];
tempa[3] = u8tmp;

2. S盒替换 (SubWord)

S盒是一个包含256个特定值的查找表。替换时，将字节的值作为索引，从S盒数组中取出对应的值。

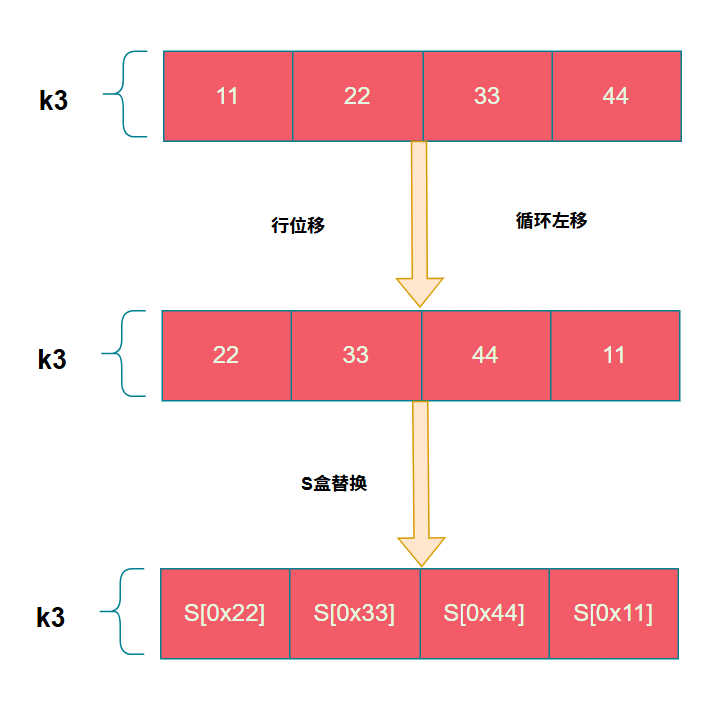
S盒替换示意图

S盒的部分数值如下，这些固定值常被用作识别AES算法的特征。

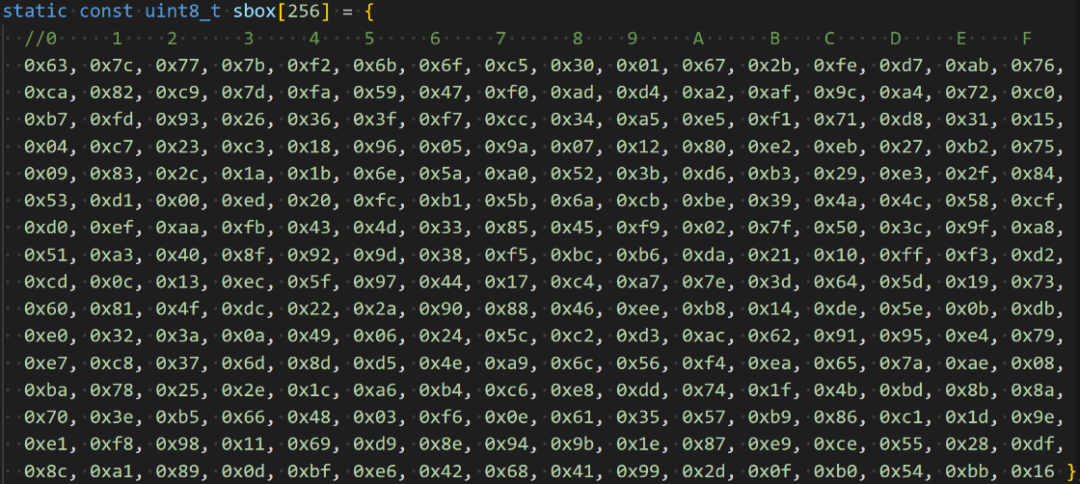
S盒数值表

代码中首先定义sbox数组，然后通过宏进行替换：

#define getSBoxValue(num) (sbox[(num)])
...
{
    tempa[0] = getSBoxValue(tempa[0]);
    tempa[1] = getSBoxValue(tempa[1]);
    tempa[2] = getSBoxValue(tempa[2]);
    tempa[3] = getSBoxValue(tempa[3]);
}

3. 与轮常数异或 (Rcon)

轮常数存储在一个名为 Rcon 的数组中。

轮常数Rcon数组

将S盒替换后的结果与轮常数异或。其中 i/Nk 代表了轮数（第1到第10轮），对应 Rcon 数组下标1到10的元素。需要注意的是，Rcon数组每个元素仅占一个字节，因此只需与密钥块的第一个字节异或。

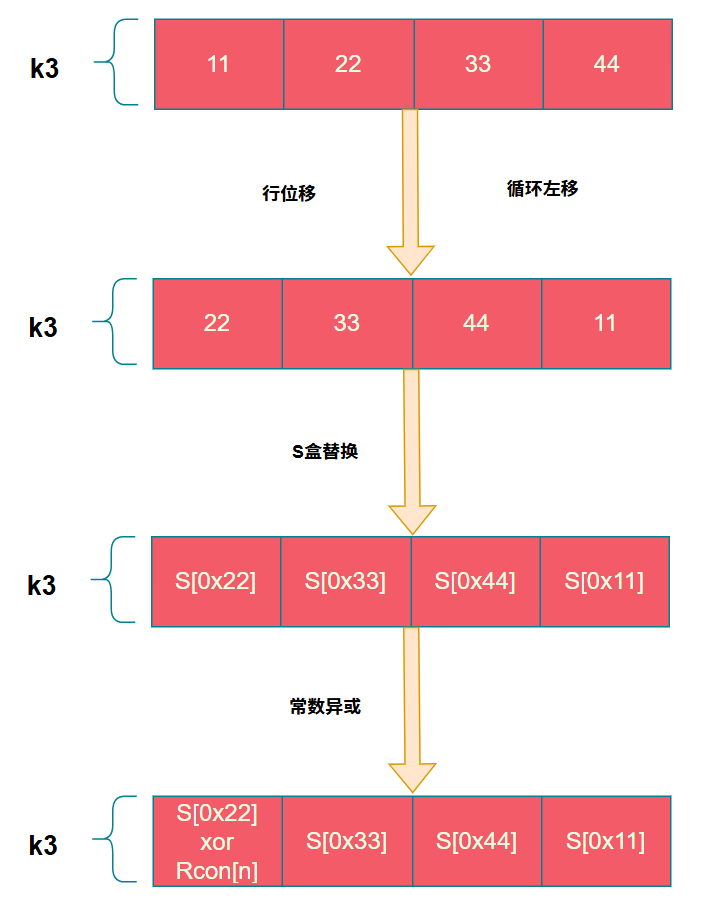
与轮常数异或

代码如下：

// 常量异或 (仅第一个字节)
tempa[0] = tempa[0] ^ Rcon[i/Nk];

完成G运算后，扩展密钥 k4 即为 G(k3) ^ k0。在代码实现中，无论当前密钥块是否经过G函数，都统一使用以下方式进行异或（若未经G函数，则 tempa 存储的就是原始的 k[i-1]）：

j = i * 4; k = (i - Nk) * 4;
RoundKey[j + 0] = RoundKey[k + 0] ^ tempa[0];
RoundKey[j + 1] = RoundKey[k + 1] ^ tempa[1];
RoundKey[j + 2] = RoundKey[k + 2] ^ tempa[2];
RoundKey[j + 3] = RoundKey[k + 3] ^ tempa[3];

加密流程

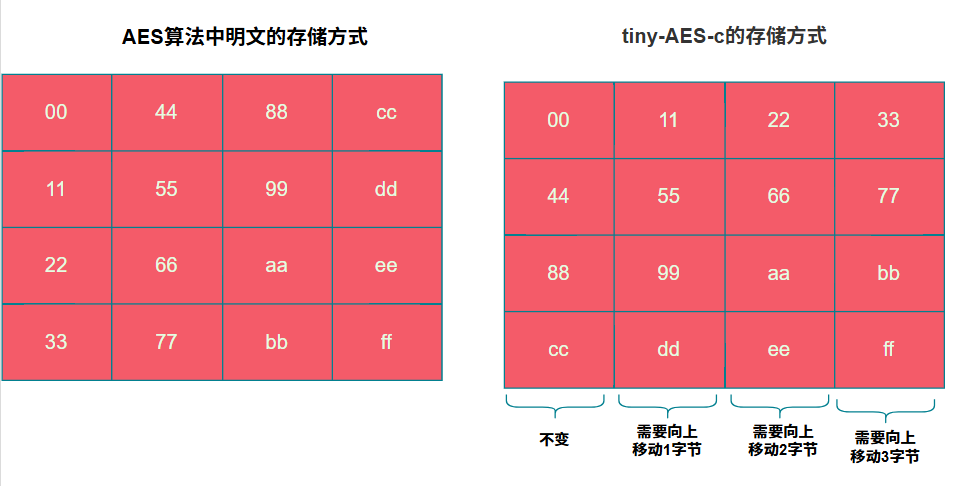
加密前，需将16字节的明文块转换为一个4x4的状态矩阵(State)，转换方式为按列填充。

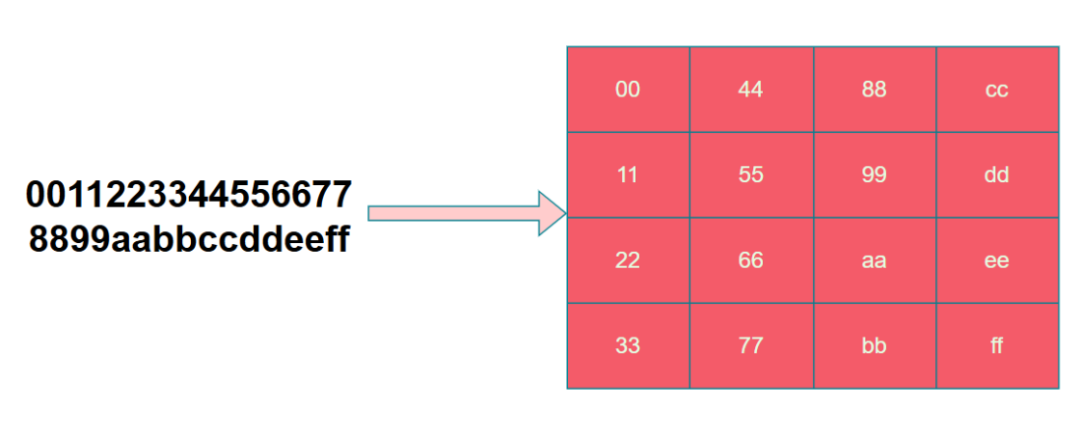
明文转换为State矩阵

完整的加密流程如下图所示，包含轮密钥加(AddRoundKey)、字节替换(SubBytes)、行位移(ShiftRows)、列混淆(MixColumns) 四个步骤，其中最后一轮不进行列混淆。

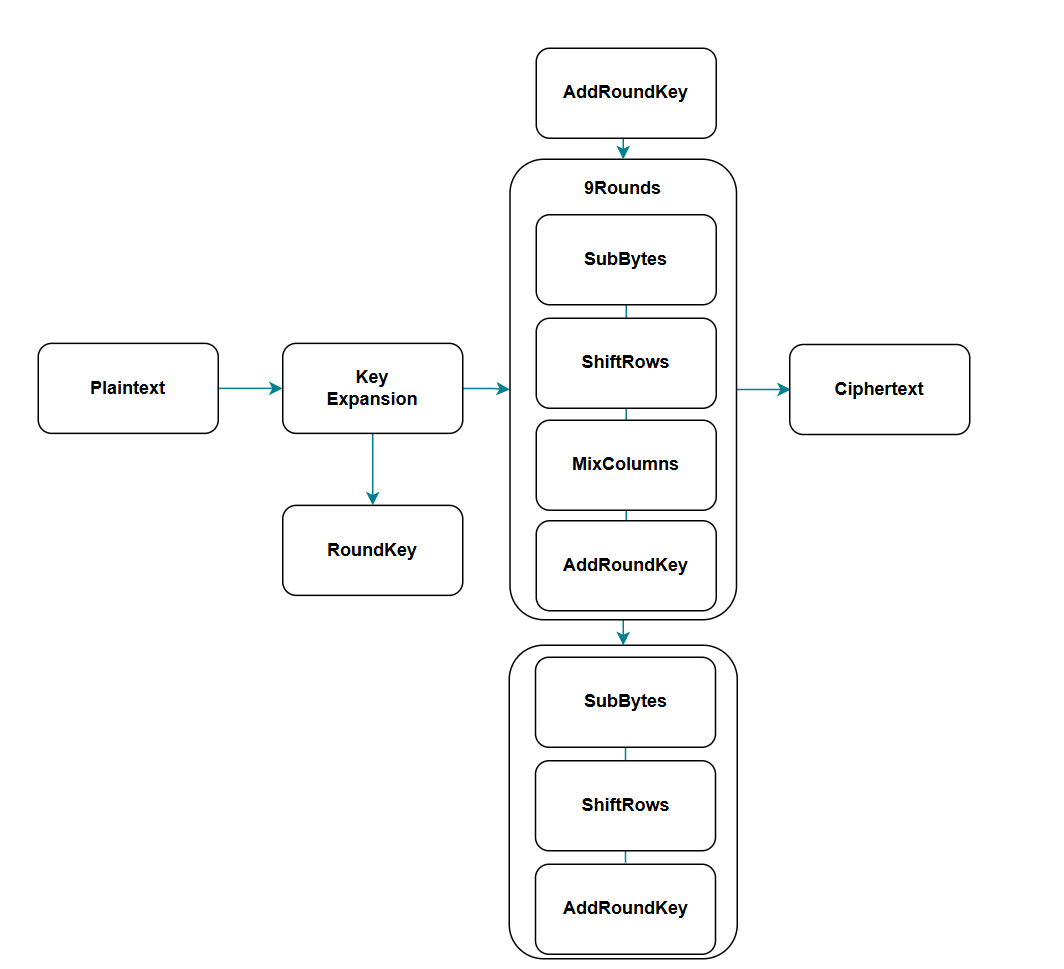
AES加密完整流程

1. 轮密钥加 (AddRoundKey)

在AES中，“加法”定义为异或(XOR)操作。轮密钥加就是将状态矩阵的每个字节与对应轮的扩展密钥字节进行异或。

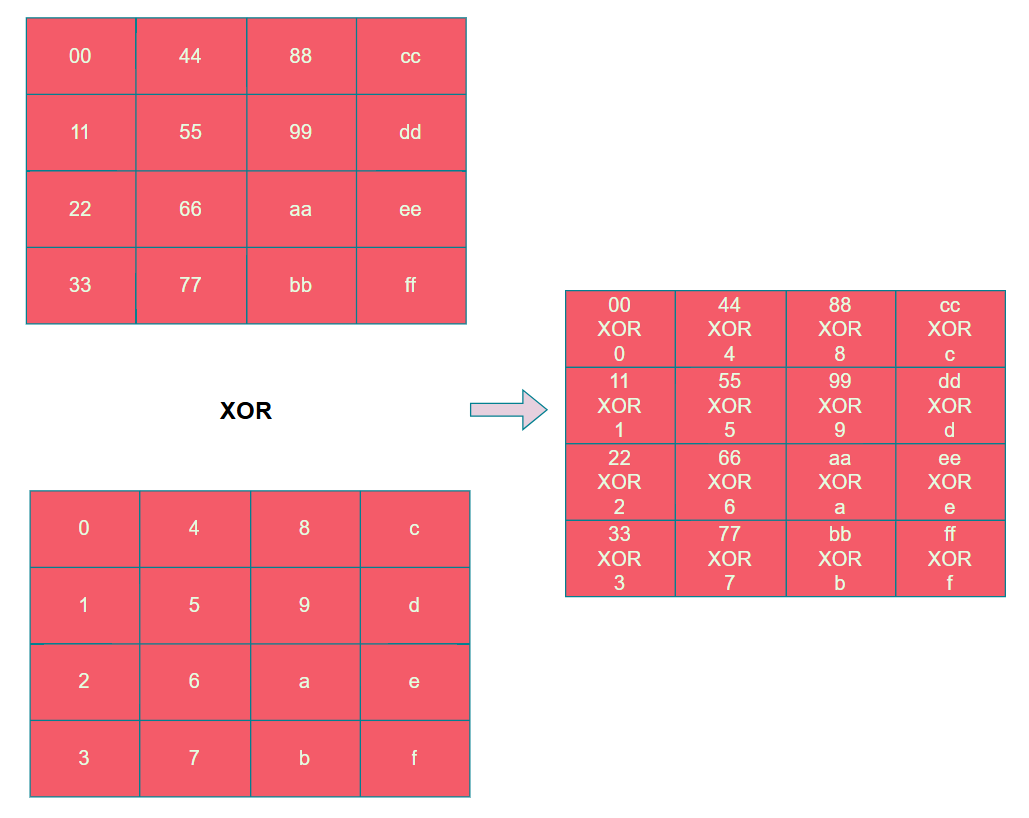
轮密钥加操作

在tiny-AES-c中，状态矩阵按行存储。轮密钥加时，按行逐字节进行异或操作，结果一致。

static void AddRoundKey(uint8_t round, state_t* state, const uint8_t* RoundKey)
{
  uint8_t i,j;
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      // 每轮密钥为16字节，计算对应密钥字节的位置
      (*state)[i][j] ^= RoundKey[(round * Nb * 4) + (i * Nb) + j];
    }
  }
}

2. 字节替换 (SubBytes)

此步骤与密钥扩展中的S盒替换完全相同，对状态矩阵中的每一个字节进行S盒查找替换。

static void SubBytes(state_t* state)
{
  uint8_t i, j;
  for (i = 0; i < 4; ++i)
  {
    for (j = 0; j < 4; ++j)
    {
      (*state)[j][i] = getSBoxValue((*state)[j][i]);
    }
  }
}

3. 行位移 (ShiftRows)

此步骤对状态矩阵的每一行进行循环左移：第0行不移，第1行左移1字节，第2行左移2字节，第3行左移3字节。

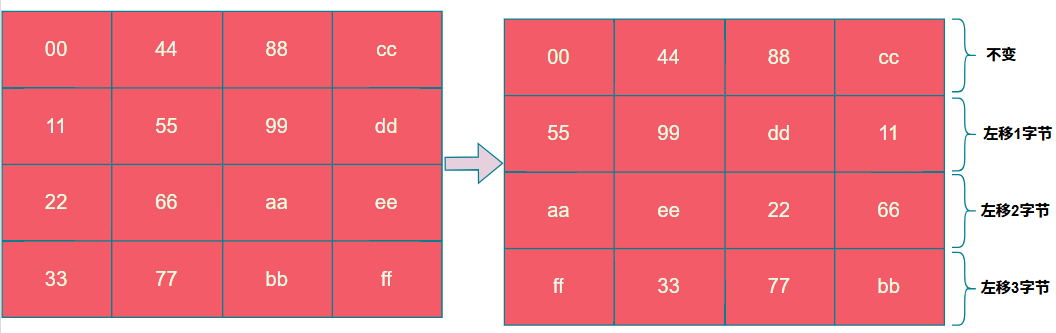
行位移操作

由于实现中状态矩阵是按行存储的，因此位移操作在代码中表现为“列方向”的上移。

static void ShiftRows(state_t* state)
{
  uint8_t temp;

  // 第1行：向上移动1个位置 (对应左移1字节)
  temp           = (*state)[0][1];
  (*state)[0][1] = (*state)[1][1];
  (*state)[1][1] = (*state)[2][1];
  (*state)[2][1] = (*state)[3][1];
  (*state)[3][1] = temp;

  // 第2行：向上移动2个位置 (对应左移2字节)
  temp           = (*state)[0][2];
  (*state)[0][2] = (*state)[2][2];
  (*state)[2][2] = temp;
  temp           = (*state)[1][2];
  (*state)[1][2] = (*state)[3][2];
  (*state)[3][2] = temp;

  // 第3行：向上移动3个位置 (对应左移3字节)
  temp           = (*state)[0][3];
  (*state)[0][3] = (*state)[3][3];
  (*state)[3][3] = (*state)[2][3];
  (*state)[2][3] = (*state)[1][3];
  (*state)[1][3] = temp;
}

理解的关键在于：当状态矩阵按行存储时，对行的“循环左移”等价于在列视图下的“循环上移”。

行位移代码解释图

4. 列混淆 (MixColumns)

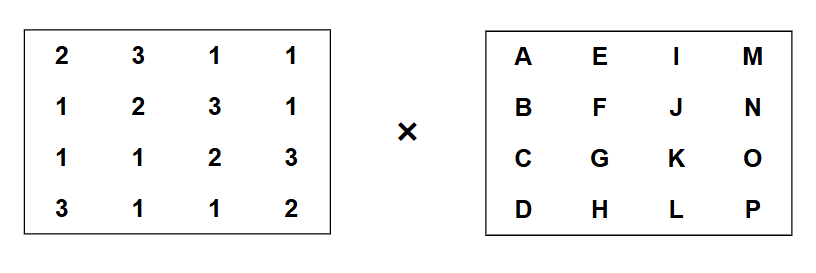
列混淆通过一个固定的矩阵与状态矩阵的每一列相乘来实现。

列混淆矩阵乘法

展开后的计算式如下（其中加法为异或）：

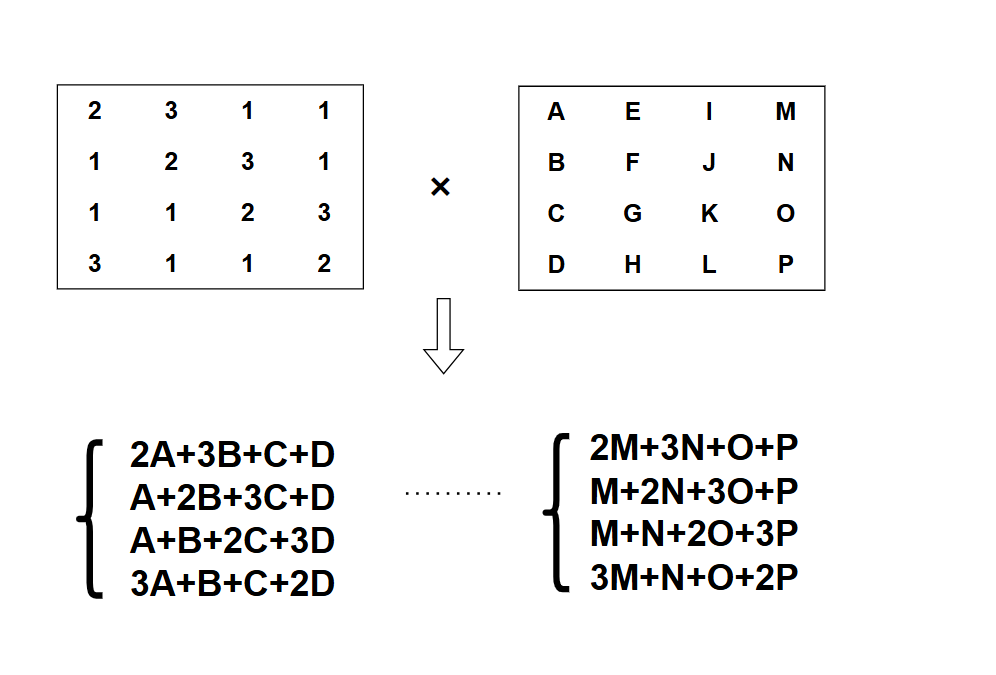
列混淆计算式

在伽罗瓦域GF(2^8)中，乘法分为三种情况（{02} 和 {03} 是常量）：

乘以 {01}：结果等于自身。
乘以 {02}：相当于将字节左移一位（值乘2），若溢出（最高位为1）则需再与 0x1b 异或。
乘以 {03}：可拆分为 {02} * x + x。

tiny-AES-c的实现采用了一种优化技巧：先计算出公共部分 A+B+C+D，再利用 xtime 函数（实现乘以{02}）来简化计算。例如，计算 S‘0,0 = {02}*A + {03}*B + C + D：

= {02}*A + {02}*B + B + C + D
= {02}*(A+B) + (A+B+C+D) + A

代码如下：

// GF(2^8)上的乘以2操作
static uint8_t xtime(uint8_t x)
{
  // 左移一位即乘2，判断最高位是否为1决定是否异或0x1b
  return ((x<<1) ^ (((x>>7) & 1) * 0x1b));
}

static void MixColumns(state_t* state)
{
  uint8_t i;
  uint8_t Tmp, Tm, t;
  for (i = 0; i < 4; ++i)
  {
    t   = (*state)[i][0]; // 保存A
    // 提前计算公共部分 A+B+C+D
    Tmp = (*state)[i][0] ^ (*state)[i][1] ^ (*state)[i][2] ^ (*state)[i][3] ;

    // 计算新状态矩阵第一列 (对应S‘0,0, S‘1,0, S‘2,0, S‘3,0)
    Tm  = (*state)[i][0] ^ (*state)[i][1] ; Tm = xtime(Tm); (*state)[i][0] ^= Tm ^ Tmp ;
    Tm  = (*state)[i][1] ^ (*state)[i][2] ; Tm = xtime(Tm); (*state)[i][1] ^= Tm ^ Tmp ;
    Tm  = (*state)[i][2] ^ (*state)[i][3] ; Tm = xtime(Tm); (*state)[i][2] ^= Tm ^ Tmp ;
    Tm  = (*state)[i][3] ^ t ;              Tm = xtime(Tm); (*state)[i][3] ^= Tm ^ Tmp ;
  }
}

逆向工程中的AES识别

下面以一道CTF逆向题 [SCTF2019]creakme 为例，演示如何在IDA的反编译代码中识别AES算法。

1. 识别密钥扩展

首先，寻找可能的密钥。发现字符串 "sycloversyclover"，长度为16字节，且被拆分为单字节数组存储。这非常符合AES-128密钥的特征。

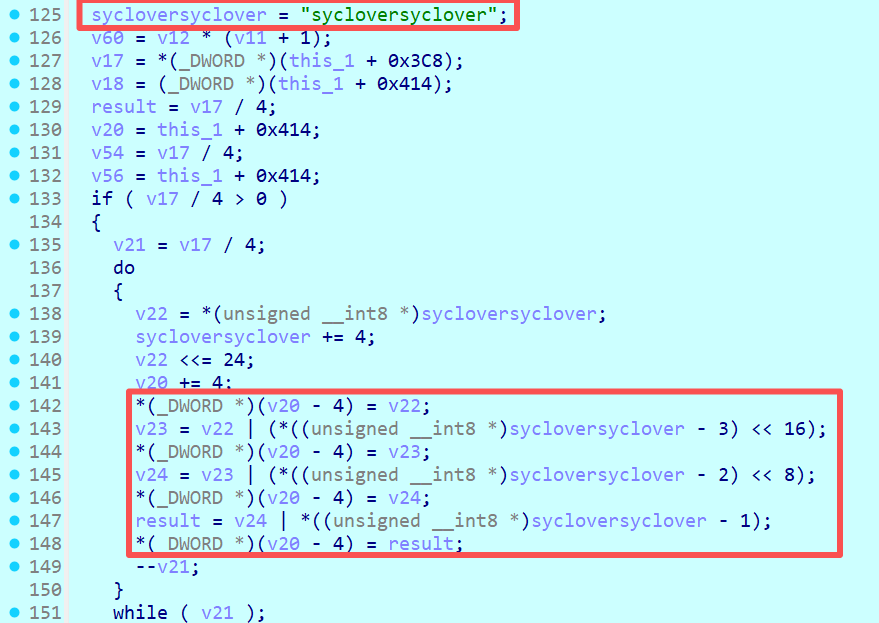
疑似密钥字符串

进一步分析，在代码中发现了S盒替换(S_BOX[v31])和循环左移(<<8)操作，这正好对应了G函数中的步骤。

G函数操作痕迹

G函数还包括与轮常数Rcon异或。跟踪变量v32，发现其指向的数据与标准Rcon表一致，从而确认了密钥扩展过程。

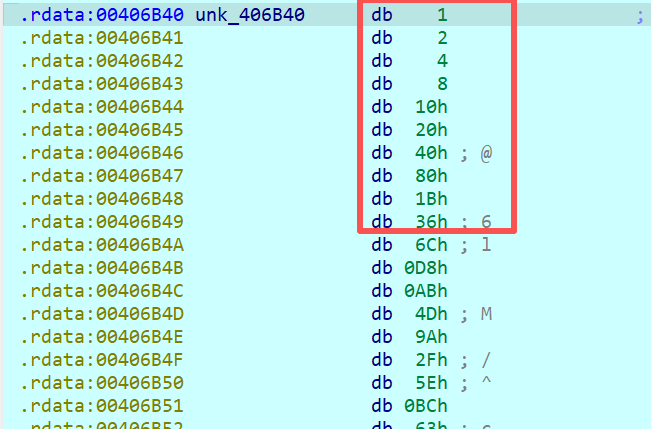
识别Rcon表

此外，密钥扩展需要生成44个4字节密钥块（共176字节）。观察循环上界，若为44，则是强提示。

2. 识别加密流程

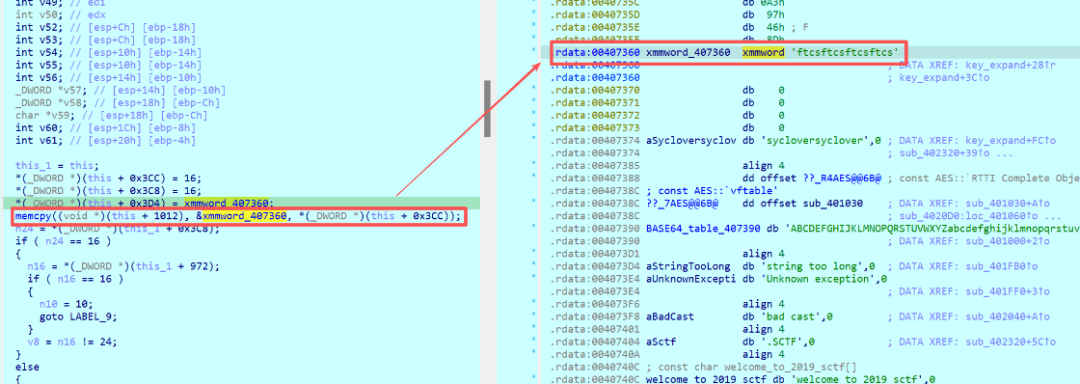
可以直接关注最后一轮加密，因为它没有列混淆操作。下图中，明显存在S盒替换和与密钥的异或操作（轮密钥加）。

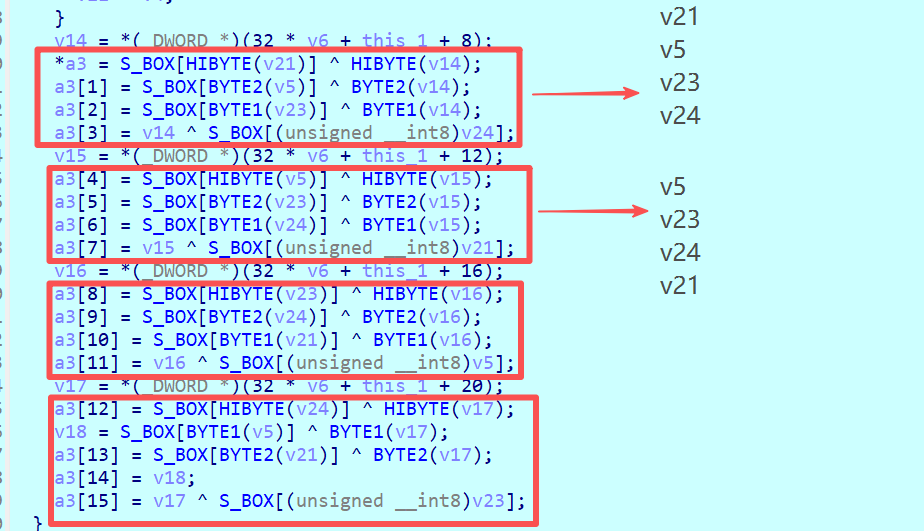
最后一轮加密操作

行位移去了哪里？注意，代码中依次对 v21, v5, v23, v24 这些int型变量（每个含4字节）进行操作。这正是一种实现方式：将状态矩阵按行存储在4个32位变量中。所谓的“行左移”，在这种存储方式下就体现为操作这些变量的顺序变化。

那么，上图之前的部分可能包含了列混淆。但其中的查表操作使用的并非S盒？

T盒实现

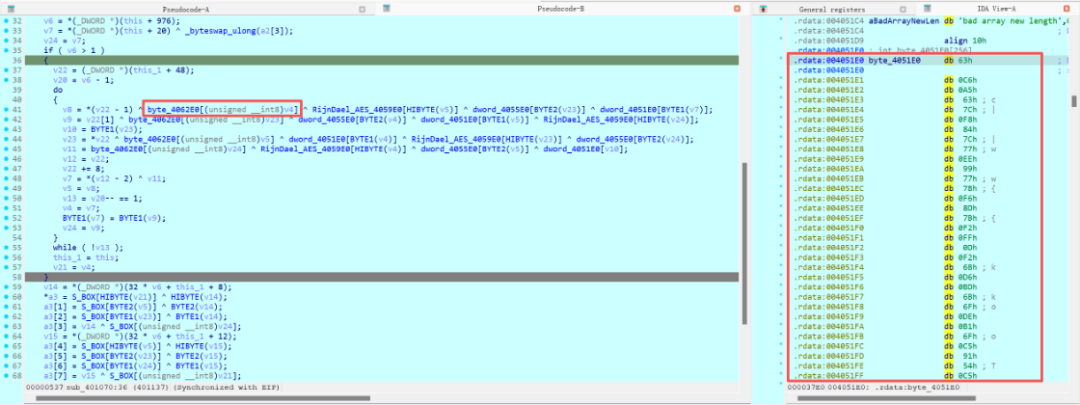
这是AES的T-table优化实现。它将 SubBytes -> ShiftRows -> MixColumns 三个步骤对于所有可能的输入字节(0-255)的最终结果预先计算好，存储在一些大表（T盒）中。加密时，直接用明文字节作为索引查T盒，一步得到三步骤的结果，以空间换取时间。因此，看到使用非S盒的大表进行查表替换，也可能是AEC算法（的优化实现）的特征。

3. 判断加密模式

识别出加密函数后，还需判断其模式。在加密函数开头，发现明文先与一个变量（如v15）异或，再进行后续处理，这强烈提示是CBC模式，而那个变量就是IV（初始向量）。

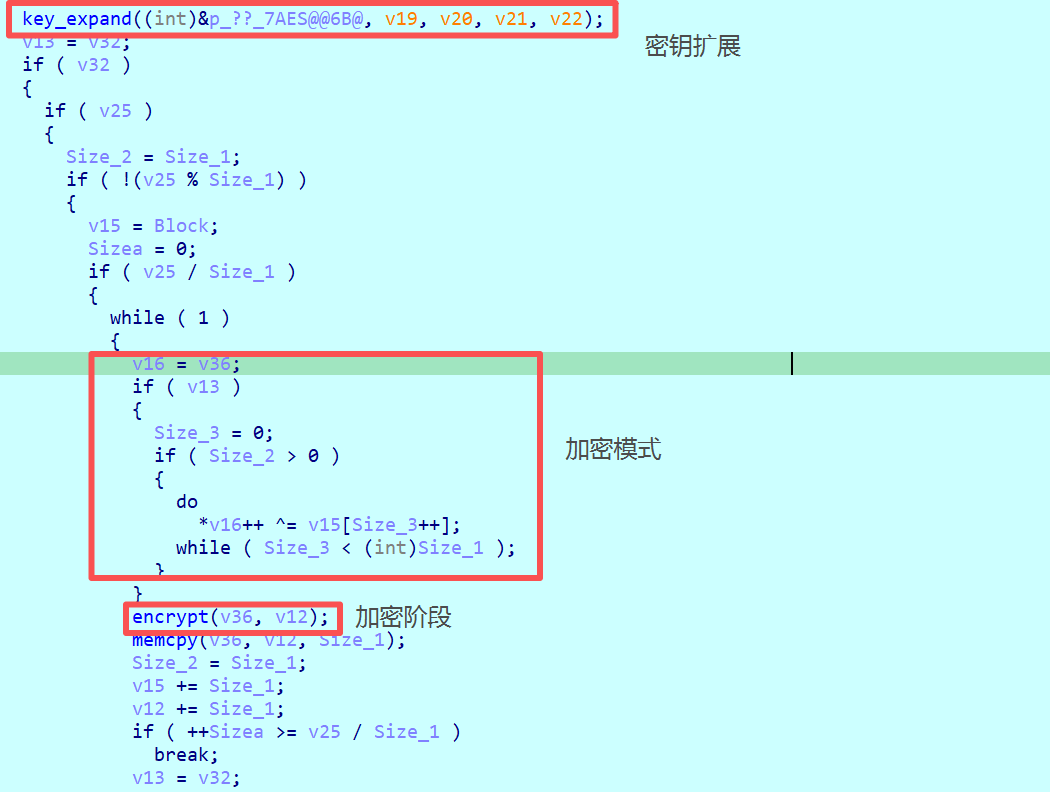
CBC模式特征

在初始化或密钥扩展相关函数中寻找IV的赋值，可以进一步确认。

IV赋值操作

总结

AES是常见的对称加密算法，熟悉其标准流程和代码实现特征，能极大提升逆向分析效率。在逆向工程实践中，可通过以下特征快速定位和分析AES算法：

密钥扩展：识别16/24/32字节的密钥常量、包含S盒查表和固定异或的循环（特别是循环次数44/52/60）。
加密流程：识别标准的轮函数结构，或使用大表（T盒）的查表操作。注意最后一轮缺少列混淆。
辅助识别：结合IDA等工具，观察固定的数据表（S盒、Rcon、T盒）、以及特定的加密模式（如CBC的IV异或）处理逻辑。

参考链接

白盒AES算法详解(一)：https://bbs.kanxue.com/thread-280335.htm
tiny-AES-c 源码：https://github.com/kokke/tiny-AES-c

上一篇：TUIOS终端窗口管理器实战指南：提升命令行多任务工作效率
下一篇：模拟地与数字地隔离：零欧电阻与导线的选择实战解析

AES, 逆向工程, C语言, IDA, 密码学