AWQ量化算法解析：4位权重存储与FP16计算的精妙实现

在深入研究大模型推理优化技术时，AWQ（Activation-aware Weight Quantization）算法以其优雅的设计思路给我留下了深刻印象。其核心思想可概括为“低精度存储，高精度计算”，旨在显著减少大语言模型（LLM）的显存占用和访存开销，同时尽可能维持模型精度。为了更直观地理解其底层原理，本文将通过一段关键的CUDA代码，剖析其将Int4权重反量化为FP16格式进行计算的过程。

这段代码展示了从单个32位整数（包含8个4位值）到uint4结构体（内含8个FP16数值）的转换过程。这种对低比特权重的精巧处理，正是众多人工智能模型加速与压缩技术的基石。

/*Adapted from https://github.com/mit-han-lab/llm-awqModified from NVIDIA FasterTransformer:https://github.com/NVIDIA/FasterTransformer/blob/main/src/fastertransformer/cutlass_extensions/include/cutlass_extensions/interleaved_numeric_conversion.h@article{lin2023awq,  title={AWQ: Activation-aware Weight Quantization for LLM Compression andAcceleration}, author={Lin, Ji and Tang, Jiaming and Tang, Haotian and Yang,Shang and Dang, Xingyu and Han, Song}, journal={arXiv}, year={2023}}*/
#pragma once
namespace vllm {
namespace awq {
__device__ uint4 dequantize_s4_to_fp16x2(uint32_t const& source) {
#if defined(__CUDA_ARCH__) && __CUDA_ARCH__ < 750
  assert(false);
#else
  uint4 result;
  uint32_t* h = reinterpret_cast<uint32_t*>(&result);
  uint32_t const i4s = reinterpret_cast<uint32_t const&>(source);

  // First, we extract the i4s and construct an intermediate fp16 number.
  static constexpr uint32_t immLut = (0xf0 & 0xcc) | 0xaa;
  static constexpr uint32_t BOTTOM_MASK = 0x000f000f;
  static constexpr uint32_t TOP_MASK = 0x00f000f0;
  static constexpr uint32_t I4s_TO_F16s_MAGIC_NUM = 0x64006400;

  // Note that the entire sequence only requires 1 shift instruction. This is
  // thanks to the register packing format and the fact that we force our
  // integers to be unsigned, and account for this in the fp16 subtractions. In
  // addition, I exploit the fact that sub and fma have the same throughput in
  // order to convert elt_23 and elt_67 to fp16 without having to shift them to
  // the bottom bits before hand.

  // Shift right by 8 to now consider elt_45 and elt_67. Issue first to hide RAW
  // dependency if we issue immediately before required.
  const uint32_t top_i4s = i4s >> 8;

  // Extract elt_01 - (i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\n"
               : "=r"(h[0])
               : "r"(i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_23 (i4s & 0x00f000f0) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\n"
               : "=r"(h[1])
               : "r"(i4s), "n"(TOP_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_45 (top_i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\n"
               : "=r"(h[2])
               : "r"(top_i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_67 (top_i4s & 0x00f000f0) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\n"
               : "=r"(h[3])
               : "r"(top_i4s), "n"(TOP_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));

  // I use inline PTX below because I am not sure if the compiler will emit
  // float2half instructions if I use the half2 ctor. In this case, I chose
  // performance reliability over code readability.

  // This is the half2 {1032, 1032} represented as an integer.
  // static constexpr uint32_t FP16_TOP_MAGIC_NUM = 0x64086408;
  // Haotian: subtract {1024, 1024} instead, we do not need to map to [-8, 7]
  static constexpr uint32_t FP16_TOP_MAGIC_NUM = 0x64006400;
  // This is the half2 {1 / 16, 1 / 16} represented as an integer.
  static constexpr uint32_t ONE_SIXTEENTH = 0x2c002c00;
  // This is the half2 {-72, -72} represented as an integer.
  // static constexpr uint32_t NEG_72 = 0xd480d480;
  // Haotian: Let's use {-64, -64}.
  static constexpr uint32_t NEG_64 = 0xd400d400;

  // Finally, we construct the output numbers.
  // Convert elt_01
  asm volatile("sub.f16x2 %0, %1, %2;\n"
               : "=r"(h[0])
               : "r"(h[0]), "r"(FP16_TOP_MAGIC_NUM));
  // Convert elt_23
  asm volatile("fma.rn.f16x2 %0, %1, %2, %3;\n"
               : "=r"(h[1])
               : "r"(h[1]), "r"(ONE_SIXTEENTH), "r"(NEG_64));
  // Convert elt_45
  asm volatile("sub.f16x2 %0, %1, %2;\n"
               : "=r"(h[2])
               : "r"(h[2]), "r"(FP16_TOP_MAGIC_NUM));
  // Convert elt_67
  asm volatile("fma.rn.f16x2 %0, %1, %2, %3;\n"
               : "=r"(h[3])
               : "r"(h[3]), "r"(ONE_SIXTEENTH), "r"(NEG_64));

  return result;
#endif
  __builtin_unreachable();  // Suppress missing return statement warning
}
}  // namespace awq
}  // namespace vllm

整个运算过程可以分为几个关键阶段。首先，代码定义了一系列掩码和用于转换的“魔法常数”。

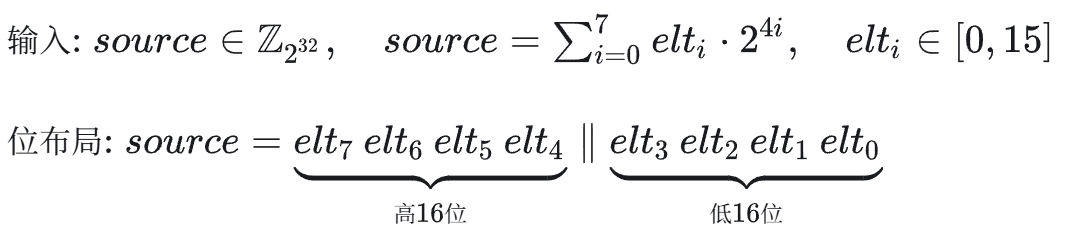
第一阶段是预处理和利用lop3指令进行数据提取。通过位运算和掩码操作，将交织在一起的8个4位整数初步分离并放入中间寄存器。

第二阶段开始进行FP16的算术转换，这是整个反量化过程的核心。对于偶数索引（如elt_01, elt_45）的数值，通过一次减法完成转换。

而对于奇数索引（如elt_23, elt_67）的数值，则通过一次乘加运算完成转换。

这里的设计精妙之处在于“魔法数”1024（对应FP16表示为0x6400）的选择。这需要从FP16的浮点数格式本身来理解：

• FP16格式：[1位符号位] [5位指数位] [10位尾数]
• 指数偏移量：15
• 实际值 = (-1)^符号位 × (1 + 尾数/1024) × 2^(指数-15)

关键在于，当一个FP16数值在1024到2048这个范围内时，其尾数每增加1，实际值也恰好增加1.0。此时，该FP16数值所能表示的最小精度正好是1.0。这与Int4整数所能表示的精度（间隔为1）完美对齐。同时，数值1024的尾数部分恰好全为0，这为原始的4位整数值（0-15）提供了完整的、无冲突的填充空间。高效地利用GPU的CUDA架构和此类数值特性，是达成低延迟推理的关键。这就是算法先将Int4整数加上1024，再转换为FP16表示的根本原因。这种利用浮点数格式特定区间的线性映射，以近乎无损的方式实现了整数到浮点数的快速转换，体现了硬件与算法协同设计的深度优化思想。