现在,众多大型模型已开始支持长文本推理,如最新的 GPT4 Turbo 能处理超过 128k 的内容,而 Baichuan2 也可应对最长为 192K 的文本。但受显存资源约束,这些模型在训练时并不一定会处理如此长的文本,其预训练阶段通常仅涉及约 4k 的内容。
因此,如何在推理阶段确保模型能处理远超预训练时的文本长度,已成为当前大型模型面临的核心问题之一,我们将此问题视为大模型的外推性挑战。
而为了应对这个挑战,最关键的地方就是如何优化大模型的位置编码。在之前的文章「绝密伏击:十分钟读懂旋转编码(RoPE)」中,已经介绍了目前应用最广的旋转位置编码 RoPE。然而,那篇文章并未涉及 RoPE 在外推性方面的表现以及如何优化其外推性。恰好最近,团队在论文分享中进一步探讨了大模型位置编码的相关内容,其中包含一些之前未曾接触的新观点。因此,本文旨在更系统地介绍位置编码及其与外推性的关系。
我们主要围绕以下两个问题展开:
- RoPE 是如何实现相对位置编码的?(是怎么“想到”的?)
- 如何通过调整旋转角(旋转角 [\omega_i = \theta_i=\frac{m}{10000^{2i/d}}]),提升长度外推效果?
本文的几个核心结论如下:
- 虽然 RoPE 理论上可以编码任意长度的绝对位置信息,但实验证明 RoPE 仍然存在外推问题——当测试长度超过训练长度后,模型效果会显著崩坏,表现为困惑度(Perplexity,PPL)等指标明显上升。
- RoPE 做线性内插(缩放位置索引,将位置 m 改为 m/k)后,通常都需要微调训练才能恢复性能。
- 直接外推的方案也可以通过微调改善,但内插方案所需的微调步数要少得多。
- NTK-Aware Scaled RoPE 可以看作一种非线性内插,本质上是修改 base(base 变成 [10000\cdot \alpha])。
- NTK-Aware Scaled RoPE 在不微调的情况下,就能取得不错的外推效果(例如只用 2048 长度训练的模型,在较低 PPL 下外推到约 8k)。
- RoPE 的构造可以视为一种 [\beta] 进制编码,在这个视角下,NTK-Aware Scaled RoPE 可以理解为对进制编码的不同扩增方式(*希望将表示范围 L 扩大到 k\L,则原本 RoPE 的 [\beta] 进制至少要扩大为 [\beta(\sqrt[d/2]{k})] 进制)。
一、绝对位置编码
先回顾绝对位置编码的基本思路。绝对位置编码通过可学习的 PositionalEmbedding 来编码位置信息:对每个位置初始化一个随机的 position embedding,然后与 word embedding 相加后输入模型。position embedding 作为模型参数的一部分,在训练过程中更新。
示意实现如下:
# 初始化
self.position_embeddings = nn.Embedding(
config.max_position_embeddings,
config.hidden_size
)
# 前向计算
position_embeddings = self.position_embeddings(position_ids)
embeddings += position_embeddings
绝对位置编码可视化

对绝对位置编码可视化后可以看到,每个位置的向量彼此区分开,相邻位置较为接近。但这个方案最大的问题也非常明显:不具备外推性,最大长度在设计时已经被固定,超出范围就无法处理。
二、正弦位置编码(Sinusoidal)
基于 Sinusoidal 的位置编码最早由谷歌在《Attention is All You Need》中提出,用于 Transformer 的位置编码。计算公式为:
[
PE{(pos, 2i)} = \text{sin}(pos / 10000^{2i/d}) \
PE{(pos, 2i+1)} = \text{cos}(pos / 10000^{2i/d}) \tag{1}
]
其中 pos 是位置,i 表示维度索引,d 是 hidden size。
乍看之下,Sinusoidal 编码似乎只是把位置通过 sin/cos 映射到 [-1, 1],但关键问题是:
- 为什么需要用 sin / cos,而不是线性函数?
- 公式中的 10000 是怎么来的?可以随便改吗?
论文中给出的性质包括:
- 相对位置表达能力:对任意固定的距离 k,PE(pos+k) 可以表示为 PE(pos) 的线性函数;
- 位置向量内积仅与相对距离 k 有关;
- 对称性:PE(t+k) 与 PE(t−k) 的内积关系对称;
- 随着 k 增大,位置向量的内积会减小,体现远程衰减。
下面分别推导这些性质。
2.1 相对位置表达能力
定义:
[
\begin{align}
PE(t, 2i) &= \sin(t \cdot w{2i}) \
PE(t, 2i+1) &= \cos(t \cdot w{2i}) \
w_{2i} &= 10000^{-2i/d}
\end{align} \tag{2}
]
对位置 t+k,有:
[
\begin{align}
PE(t+k, 2i) &= \sin((t+k)w{2i}) \
&= \sin(tw{2i})\cos(kw{2i}) + \cos(tw{2i})\sin(kw_{2i}) \
&= PE(t, 2i)\cdot PE(k, 2i+1) + PE(t, 2i+1)\cdot PE(k, 2i)
\end{align} \tag{3}
]
[
\begin{align}
PE(t+k, 2i+1) &= \cos((t+k)w{2i}) \
&= \cos(tw{2i})\cos(kw{2i}) - \sin(tw{2i})\sin(kw_{2i}) \
&= PE(t, 2i+1)\cdot PE(k, 2i+1) - PE(t, 2i)\cdot PE(k, 2i)
\end{align} \tag{4}
]
在这两个式子中,对固定的 k,[PE(k, 2i), PE(k, 2i+1)] 都是常数,因此:
- [PE(t+k)] 可以用 [PE(t)] 的线性组合表示;
- 换言之,Sinusoidal 实际是为网络显式提供“可线性推导”的相对位置信息。
2.2 内积仅与相对位置 k 有关
Attention 的一个核心运算是向量内积。考虑两个位置 t 与 t+k 的位置向量内积:
[
\begin{align}
PE(t)\cdot PE(t+k)
&= \sum_{i=0}^{d/2-1} PE(t, 2i)PE(t+k,2i)
- \sum{i=0}^{d/2-1} PE(t, 2i+1)PE(t+k,2i+1) \
&= \sum{i=0}^{d/2-1} \sin(tw{2i})\sin((t+k)w{2i})
- \sum{i=0}^{d/2-1} \cos(tw{2i})\cos((t+k)w{2i}) \
&= \sum{i=0}^{d/2-1} \cos(kw_{2i})
\end{align} \tag{5}
]
最终内积只剩下关于 k 的项,与绝对位置 t 无关,因此内积仅由相对距离 k 决定。
进一步可以推到 [PE(t+k)\cdot PE(t) = PE(t)\cdot PE(t-k)],说明 Sinusoidal 具有关于位置差的对称性。
2.3 远程衰减
从公式(5)可以看到,随着 k 的增大,[\cos(kw_{2i})] 在不同频率叠加后整体会趋于衰减,从而使得远距离位置的内积较小,体现出远程衰减——注意这是对“位置编码内积”的数学性质。
图2-1 随着相对距离k的增加,位置向量内积PE(t)PE(t+k)逐渐降低
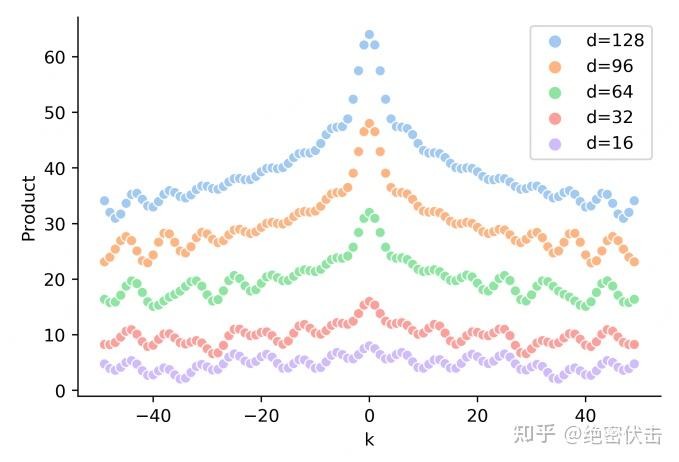
不过,在实际 Transformer 中,我们真正用到的是 [PE] 经过线性变换后的 [q,k] 向量,以及 [q^\top k] 这一结果。下文会看到:在加入可学习的投影矩阵 [W_q, W_k] 后,这种理想的“只与 k 有关”的性质往往会被破坏。
2.4 base=10000 从何而来?
为什么 [\theta_i] 要用 [10000^{2i/d}] 这一形态?一个常见的解释方式是从周期角度出发。
对第 i 对维度([\sin, \cos]),其角频率为 [w_{2i} = 10000^{-2i/d}],对应的周期是:
[
Ti = \frac{2\pi}{w{2i}} = 2\pi \cdot 10000^{2i/d}
]
图2-2 不同base下的position embedding取值
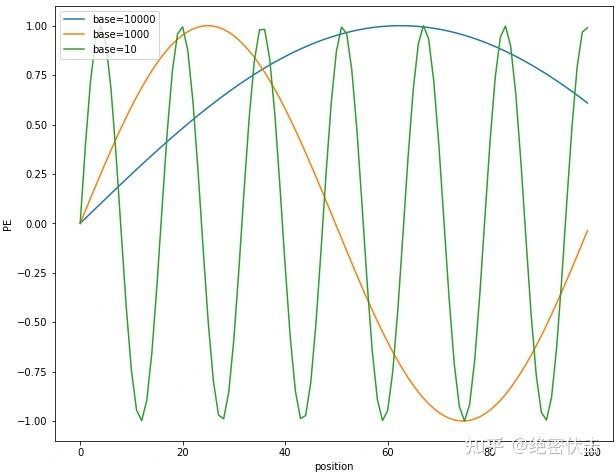
随着 i 增加,周期在指数级拉长。假设 [i \in [0, d/2)],则 [T_i \in [2\pi,\ 10000\cdot 2\pi]]。也就是说,Sinusoidal 编码用从高频到低频的一系列正弦波叠加,来唯一标识位置。
如果 base 太小,周期范围非常有限,长序列中不同位置很容易出现周期重复;base 较大时,在常见的长度范围(比如 0~1024)内,仍处于周期的一小段,不易重叠,更利于区分位置。
直观理解:base 越大,位置编码在“可见长度范围内”变化得更慢,每个位置的向量更“独特”。
2.5 Sinusoidal 是否真的具备外推性?
从纯数学角度看,Sinusoidal 编码只依赖相对位置 k,似乎具备理论上的“长度外推性”。但在真实的自注意力中,Attention 计算的是:
[
\text{Att}(t,s) \propto
(PE_t + x_t)^\top W_q^\top W_k (PE_s + x_s)
]
或者只考虑纯位置项:
[
PE_t^\top W_q^\top Wk PE{t+k}
]
有了投影矩阵 [W_q,W_k] 后,模型可能把位置编码维度“扭曲”为各种组合的特征,最终内积不再仅由“位置差”决定。实际可视化时,会发现真实的 [qt^\top k{t+k}] 与 k 的关系,不再具有理想的远程衰减性质,说明:
- Sinusoidal 在编码层面具备漂亮的相对位置与外推性质;
- 但经过可学习线性变换后,这些性质未必能完整“传递到”注意力行为中。
图2-3 真实的q,k向量内积和相对距离之间,没有远程衰减性
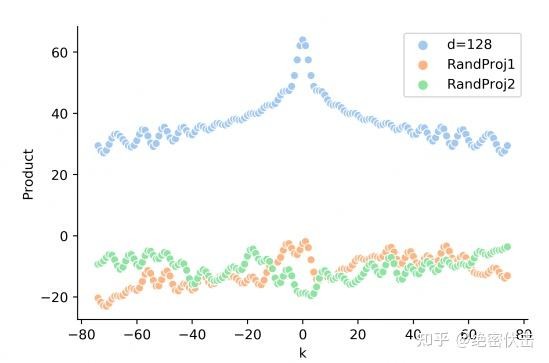
这也是后来 RoPE 等方案试图“直接作用在 q/k 上”的动机之一。
三、旋转位置编码(RoPE)
3.1 什么是“好的”位置编码?
从长上下文大模型的视角,一个理想的位置编码应满足:
- 每个位置有唯一编码(可区分);
- 对超过训练长度的序列具备良好的外推性;
- 任意两个 token 之间的相对距离感知一致:
若在样本 A 与样本 B 中,两个 token 之间的距离同为 k,则两者的相关性模式应尽量一致。
第三点可以理解为位置编码的平移不变性:只关心距离,不关心在句子中的绝对偏移。
图3-1 平移性
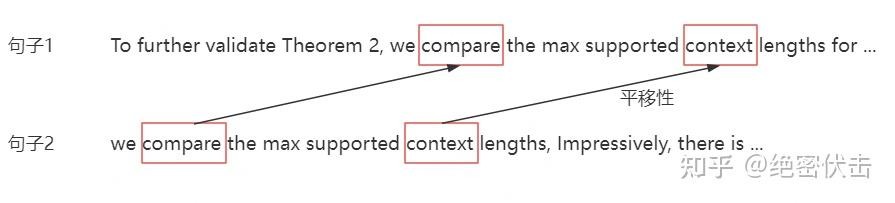
RoPE 正是针对上述目标设计的一种相对位置感知且可外推的编码。
3.2 RoPE 如何“把绝对位置变成相对位置内积”?
RoPE(Rotary Position Embedding)由苏神在 RoFormer 论文中提出,目前已成为大多数主流 LLM 的标配。它的关键点是:
- 不再对 embedding 直接相加位置向量;
- 而是在计算 q、k 后,按照每 2 维一组,对向量做一个位置相关的 2D 旋转。
设位置 m 的 query 为 [\bm{q}_m],位置 n 的 key 为 [\bm{k}_n]。传统绝对位置编码形式下:
[
\begin{align}
\langle f_q(x_m, m), f_k(x_n, n) \rangle
&= q_m^\top k_n \
&= x_m^\top W_q^\top W_k x_n +
\underbrace{
x_m^\top W_q^\top W_k p_n +
p_m^\top W_q^\top W_k x_n +
p_m^\top W_q^\top W_k pn
}{\text{显式依赖 }m,n}
\end{align} \tag{6}
]
可以看到,多出来的三项都显式依赖于绝对位置 m,n,无法被写成只依赖 m−n 的函数,因此难以满足“只由相对距离决定”的特性。
RoPE 的思想:我们希望存在一种变换,使得:
[
\langle f_q(x_m, m), f_k(x_n, n) \rangle
= g(x_m, x_n, m-n) \tag{7}
]
也就是说,attention 打分只依赖于 token 内容与相对距离 m−n。
为此,RoPE 将每个 2 维子空间视为一个复数平面,对 [\bm{q}_m,\bm{k}_n] 施加如下变换(简化到 2 维):
[
f_q(x_m,m) = R(m\theta)\,W_q x_m, \quad
f_k(x_n,n) = R(n\theta)\,W_k x_n
]
其中 [R(\cdot)] 为 2×2 旋转矩阵:
[
R(m\theta) =
\begin{pmatrix}
\cos(m\theta) & -\sin(m\theta) \
\sin(m\theta) & \cos(m\theta)
\end{pmatrix} \tag{9}
]
在多维情况下,将 hidden 维度按 2 维一组分块,对每一对维度使用一组不同的旋转角度 [\theta_i],整体旋转矩阵为分块对角形式:
[
\bm{R}^d_{\Theta,m} =
\begin{pmatrix}
R(m\theta_0) & & & 0 \
& R(m\theta1) & & \
& & \ddots & \
0 & & & R(m\theta{d/2-1})
\end{pmatrix} \tag{10}
]
其中:
[
\Theta = { \theta_i = 10000^{-2i/d},\ i=0,...,d/2-1}
]
也就是说,RoPE 在每个 2 维子空间上顺时针旋转 [m \theta_i],对应到复数表示即是乘上 [e^{i m\theta_i}]。对 key 做的是乘上共轭角旋转 [e^{i n\theta_i}](或等价操作),于是它们的内积就自然带出了 [(m-n)\theta_i],从而把“绝对位置”转为了“相对位置差”。
为什么想到用 [e^{im\theta}] ?
从复数乘法性质看:
[
e^{im\theta} \cdot e^{-in\theta} = e^{i(m-n)\theta}
]
即“相乘后角度相减”。如果把不同位置的 q、k 都各自乘上自己的相位,则在计算内积时天然会出现与差值 m−n 相关的相位。因此用复指数(或等价的旋转矩阵)是一个非常自然的选择:结构精简,运算高效,还能与 Sinusoidal 编码一脉相承。
图3-2 为什么RoPE选择e^{im}方式进行位置编码

3.3 RoPE 的远程衰减
图3-3 RoPE的远程衰减
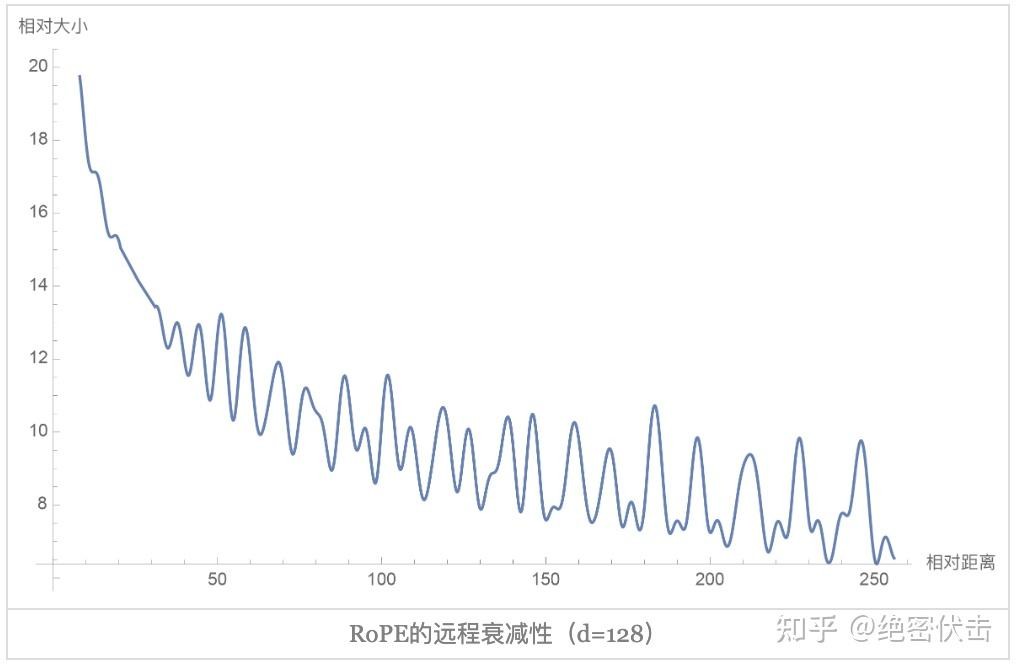
在 RoPE 下,对不同距离 [|m-n|] 的 [q_m^\top k_n] 做可视化,可以发现:
随着相对距离增大,注意力打分整体有衰减趋势,体现了类似 Sinusoidal 的“远程衰减”。
对应角度参数通常依旧选取:
[
\theta_i = 10000^{-2i/d}
]
即直接沿用 Sinusoidal 的频率分布。论文中曾尝试将 [\theta_i] 设为可训练参数,以 [10000^{-2i/d}] 初始化并训练一段时间,发现训练后 [\theta_i] 变化不大,说明这一手工设定在实践中已经相当合理,因此后续工作基本都直接固定这一形式。
四、通过调整旋转角提升外推效果
即便 RoPE 从构造上支持任意长位置编码,实验证明:
当推理长度显著超过训练长度时,模型的 PPL 等指标仍会出现明显“崩坏”,这说明 RoPE + 预训练长度的组合依然存在实际的“外推边界”。
为突破这一边界,社区中出现了大量“扩展上下文窗口”的工作,其中较有代表性的有:
- 位置线性内插(Position Interpolation, PI):Meta 在《Extending Context Window of Large Language Models via Positional Interpolation》中系统提出;
- NTK-Aware Scaled RoPE:社区工作,从 NTK 与频域视角对 RoPE 的 base 做非线性缩放。
二者的共通点是:直接修改 RoPE 的旋转角或其参数,而不是改动网络主体结构。
在详细计算之前,可以顺带指出:这一类工作与大模型中的 LLM / Transformer 结构密切相关,如果你对 Transformer 编码器结构还不够熟悉,可以配合一些人工智能 / LLM 基础资料一起阅读,更容易把“数学公式”和“具体代码实现”对应起来。
4.1 位置线性内插(Position Interpolation, PI)
RoPE baseline 情况下,当直接把训练长度 2048 的模型拿去在 4096、8192 上推理,会发现 PPL 很快恶化,说明“纯外推”效果有限。位置线性内插的核心思路非常简单:
图4-1 RoPE 位置线性内插(base和位置线性内插的效果对比)
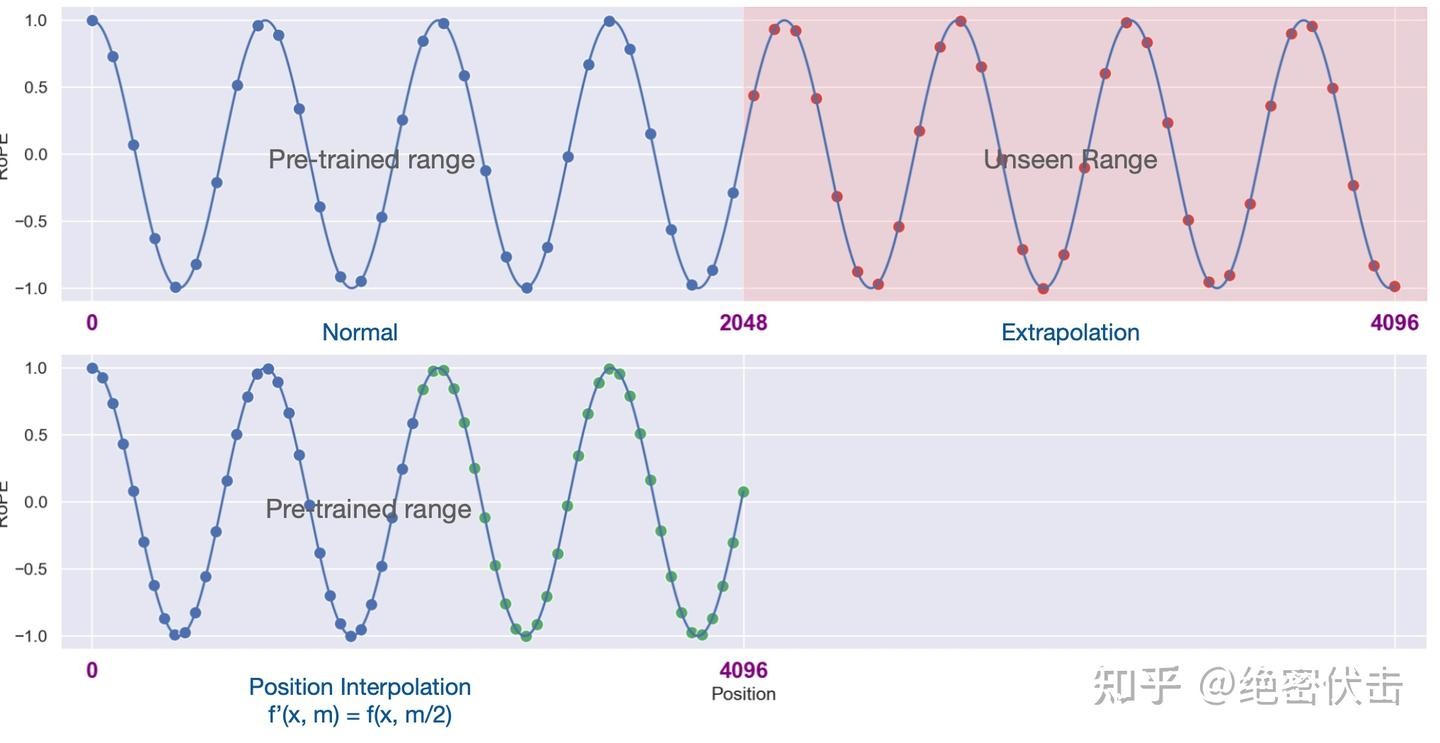
不改变 RoPE 的频率分布,而是“拉伸/压缩位置索引”。
用一行公式概括:
[
f'(x, m) = f\left(x, \frac{mL}{L'} \right) \tag{12}
]
其中:
- L:训练时的最大长度(如 2048);
- L':推理时实际的长度(如 4096、8192);
- [\frac{mL}{L'}] 将原本在 [0, L'] 区间的 m 线性缩放到 [0, L] 范围内。
这样做的效果是:
- 在长序列推理时,所有位置索引都被映射回模型“见过”的长度区间内;
- 不需要改变 RoPE 的 base 与频率分布,只是把“长序列”压缩到“训练长度”的频域中;
- 代价是:相邻位置的间隔变小,编码更“拥挤”,需要少量长文本数据对这种密集映射进行微调。
以 base = 10000, d = 2048 为例,对第 2000 维(即某一对 [\sin,\cos] 对应的频率):
[
RoPE = \sin\left(m\cdot 10000^{-2000/4096}\right) \tag{11}
]
图4-2 RoPE位置编码
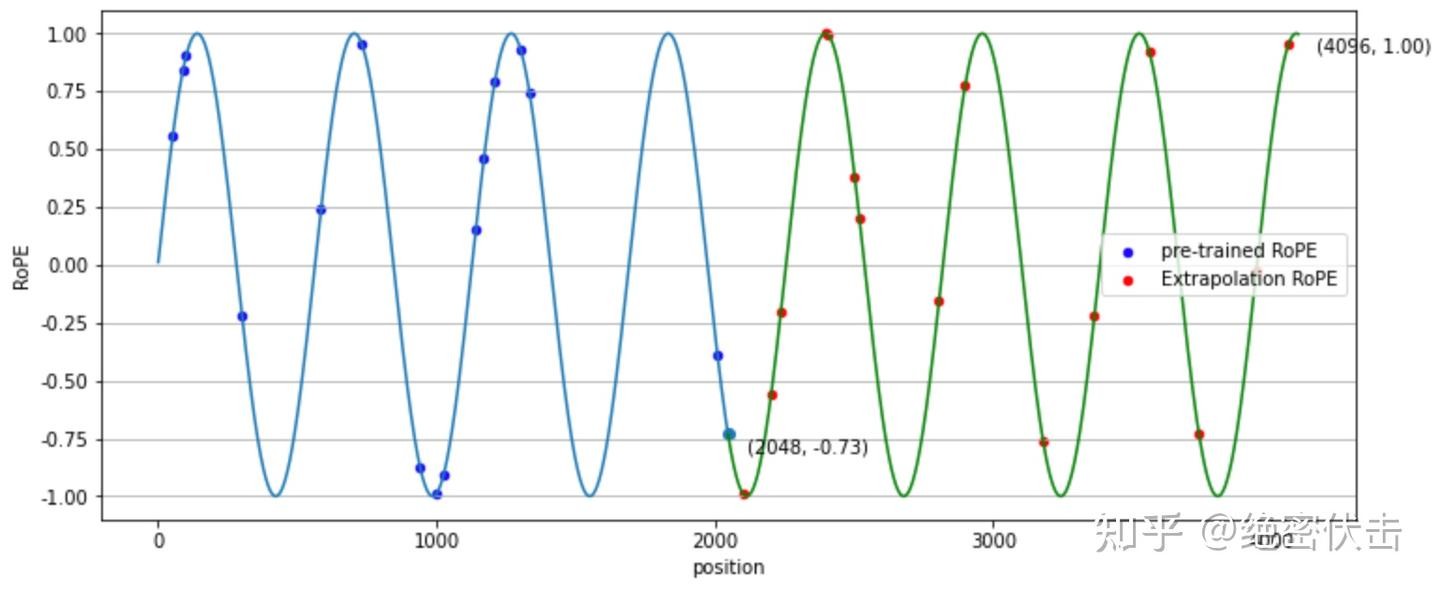
如果训练长度是 2048,而推理长度是 4096,则通过 PI 把 4096 映射到 [0, 2048] 区间后,等价于用更“缓慢”的位置变化在更长区间覆盖原有频率范围。这可视作频域上的一种线性压缩。
PI 的实验证据:
- 在不微调的情况下,单纯位置线性内插会让长序列 PPL 很差(甚至比直接外推更糟);
- 但只要用极少量长文本样本微调很少步数,就能将上下文扩展到 8k 甚至更长,且 PPL 维持在可接受水平。
图4-3 微调少量长文本,位置线性内插就能推理长文本
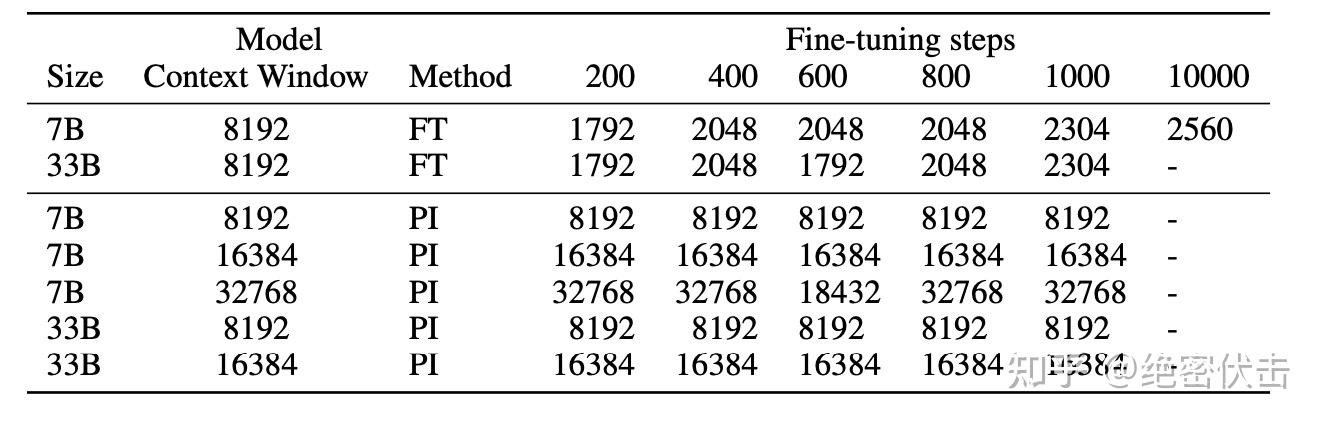
4.2 NTK-Aware Scaled RoPE:非线性“进制扩展”
位置线性内插是线性缩放位置索引,从“输入侧”下手;NTK-Aware Scaled RoPE 则从“频率侧”——也就是 RoPE 的 base——下手。
设标准 RoPE 的角频率为:
[
\theta_i = 10000^{-2i/d}
]
NTK-Aware Scaled RoPE 将其替换为:
[
\theta_i = (10000\cdot \alpha)^{-2i/d} \tag{15 中的形式}
]
其中 [\alpha] 是一个大于 1 的缩放因子(与目标扩展倍数 k 相关)。
直观上,这就是把 RoPE 中的“底数”从 10000 提高到了 [10000\cdot \alpha],从而减小所有频率(让周期更长),在长序列上“拉平”旋转速度:
- 高频部分(小 i)从外推视角看更“保守”;
- 低频部分决定了“最全局”的位置变化,其频率被减小,相当于在新长度下仍停留在较慢变化区域。
更有趣的是,从苏神提出的“RoPE = [\beta] 进制编码”视角看,NTK-Aware Scaled RoPE 等价于:
如果想把原本能表示长度 L 的 [\beta] 进制编码扩展到 k*L,则最小需要把进制提高到 [\beta(\sqrt[d/2]{k})] 级别。
这种“进制扩展”的好处在于:
- 不需要改变向量维度(仍然是 d 维);
- 每一位“权重”的进制一致(不会像线性内插那样只让某些维度更“挤”);
- 在不微调或极少微调的情况下,就可以在更长的上下文上保持较为平稳的 PPL。
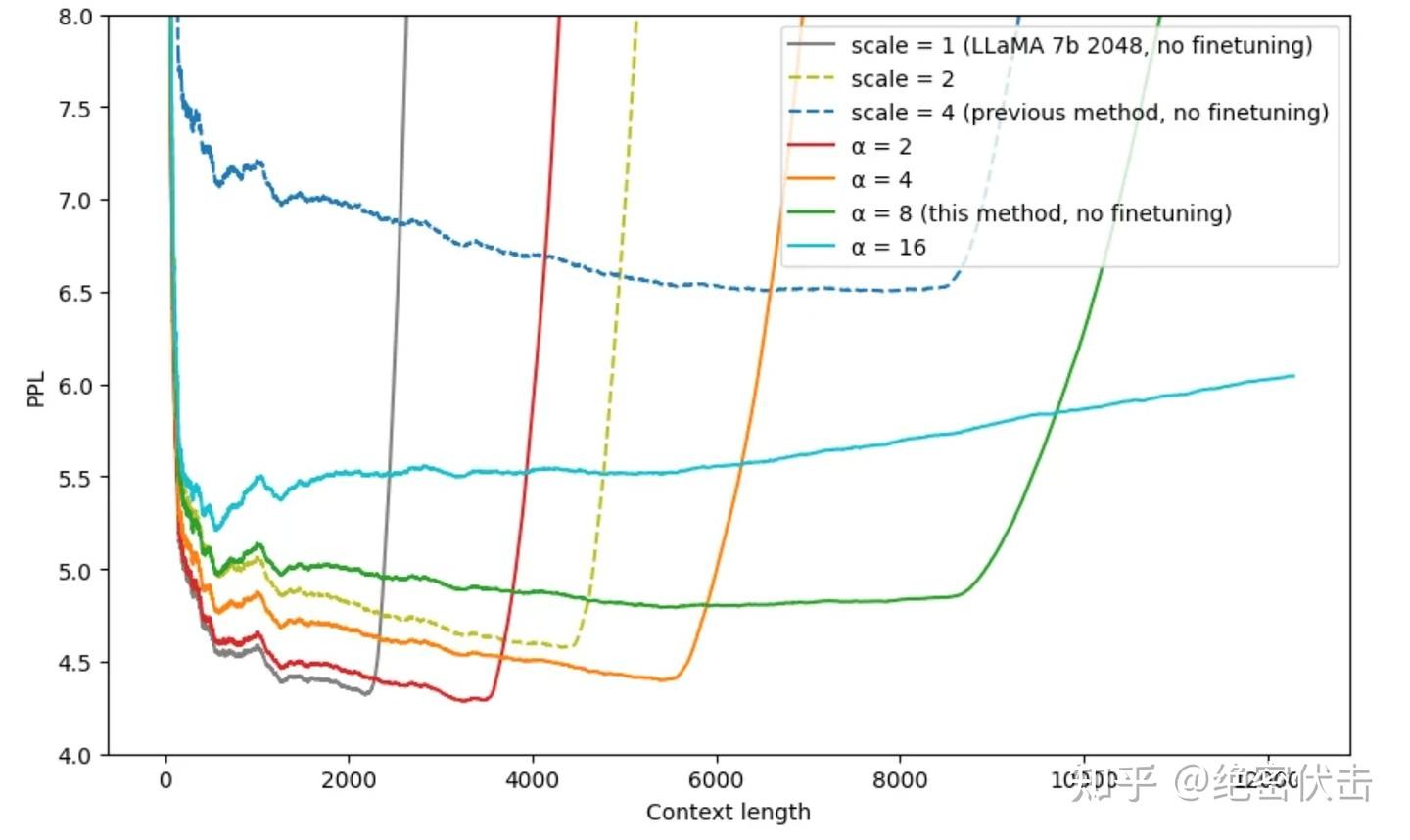
NTK-aware Scaled RoPE 在 LLaMA-7B(训练 context = 2048)上的实验中表明:
- 在完全不对 4096 上下文进行微调的前提下,通过合理的 [\alpha] 选取,可以把 PPL 降到很低;
- 实际表现远好于直接外推与“未调参的 PI”。
对 RoPE 做进制化理解后,三种方案的关系可以总结为:
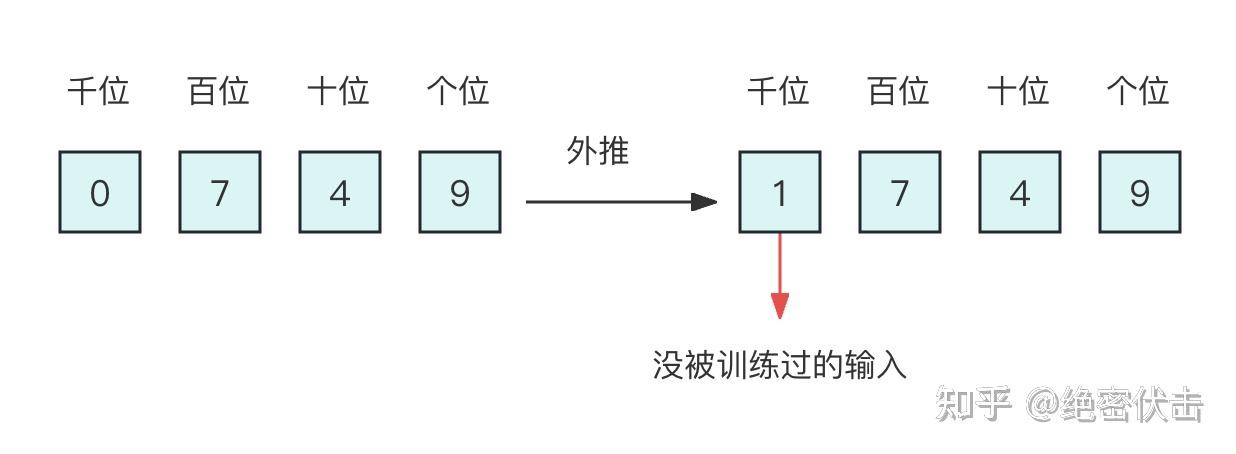
图4-4 直接外推
位置线性内插
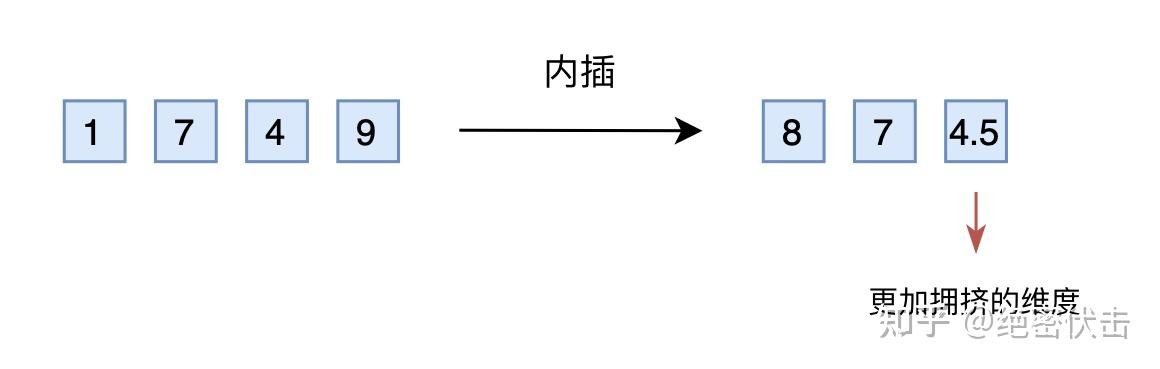
图4-5 进制转换
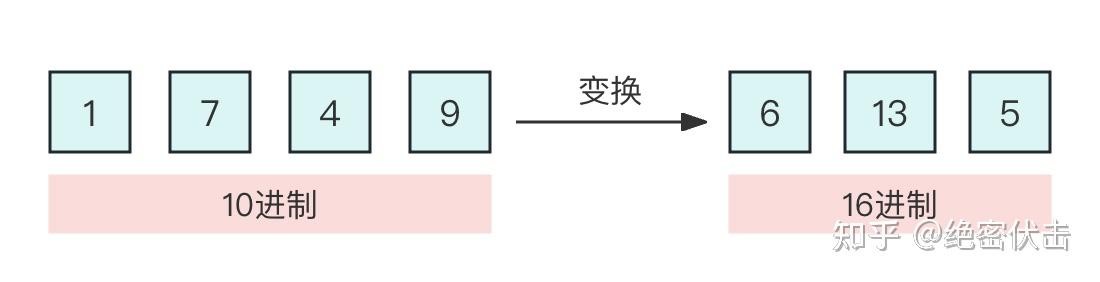
图4-6 不同插值方法的效果(这里的scale是指位置插值中扩大的倍数k,alpha是指NTK中的lambda参数或者是公式 ...
- 直接外推:不改任何参数,外推压力集中在“高位”,训练期未充分学习这些部分;
- 位置线性内插(PI):从“输入位置 m”侧压缩,使“低位”信息更稠密,需要微调以适应不同维度之间的分布变化;
- NTK-aware Scaled RoPE:从“进制 / base”侧扩展,让表示空间整体从 [\beta] 进制平滑扩展为 [\beta(\sqrt[d/2]{k})] 进制,在序信息比较规则保持一致的前提下,把外推压力均匀摊在所有“位”上,因此可做到几乎不需微调就能外推。
五、对比:外推、线性内插与 NTK 扩展
以训练长度 512、测试长度 4096(k=8)为例(准确率):
| 测试长度 |
512(训练) |
4096(外推) |
| Baseline 直接外推 |
49.91% |
23.16% |
| PI-RoPE(位置线性内插,未微调) |
49.91% |
13.54% |
| NTK-RoPE(不微调) |
49.41% |
39.27% |
可以看到:
- 直接外推:长 context 下准确率大幅下降;
- 线性内插 + 不微调:长 context 下更差,这是因为仅修改位置索引但未让模型适应新的“拥挤映射”;
- NTK-RoPE + 不微调:在长 context 下准确率显著优于前两者,说明“进制扩展”对模型的破坏最小。
如果再配合少量长文本微调(例如 1000 条样本),PI-RoPE 和 NTK-RoPE 都可以进一步提升,上下文窗口可以扩展到 8k 甚至更长。
六、小结
围绕“大模型位置编码与外推性”,本文梳理了以下关键点:
- 绝对位置编码不具备外推性,最大长度在设计时就被硬编码。
- Sinusoidal 编码在数学上具备相对位置表达、对称性、远程衰减等漂亮性质,但经过可学习投影矩阵后,这些性质往往不能完全保留下来。
- RoPE 通过对 q/k 做位置相关的二维旋转,使 attention 打分显式依赖于相对距离 m−n,从机制上逼近“理想相对位置编码”。
- 实验表明,单纯依赖 RoPE 仍然存在“训练长度→推理长度”的外推崩坏问题。
- 位置线性内插(PI)通过缩放位置索引,把长序列“压”回训练长度范围,在很少的长文本微调下就能很好扩展上下文窗口,但不微调时表现较差。
- NTK-Aware Scaled RoPE 从“进制 / base”角度修改 RoPE,将 [10000] 扩展为 [10000\cdot \alpha],在不改变序信息比较规则的前提下扩展可表示长度,实践中可以在不微调或极少微调下获得优秀的长上下文效果。
- 在“RoPE = [\beta] 进制编码”的视角下:
- 直接外推 ≈ 使用原进制在更大范围硬撑;
- 位置内插 ≈ 用同一进制表示更大范围,但低位更拥挤;
- NTK 扩展 ≈ 提升进制基数,让范围和分辨率同步扩展,更符合大模型依赖“相对距离与序”的特性。
随着 GPT-4 Turbo、Baichuan2 等大模型不断提升上下文长度,如何不显著增加预训练成本,又能稳定扩展上下文窗口,将会在相当长一段时间内继续是 LLM 研究和工程实践的核心问题之一,而位置编码与外推性正是其中最关键的基础模块之一。
转自 知乎专栏 作者 绝密伏击