联合分布与边缘分布的核心解析：从概念、性质到机器学习应用

在多维不确定性的分析中，人们往往试图寻找一种方式，使随机变量的关系能够被严谨地描述。在经典概率框架内，单一随机变量的概率表现并不能充分揭示多变量体系的全貌。随着统计学、机器学习、计量模型和实验科学的深入发展，研究者愈发关注多个变量之间的相互影响机制，而不仅仅是个体层面的概率特征。在这种背景下，联合分布与边缘分布成为理解多变量结构的关键概念。

当我们探讨复杂系统时，无论是高维数据集中的变量互动、量化模型中的收益结构，还是实验测量中的多维数据点，都不可避免地涉及多个随机变量的同时表现。此时，若仅观察单个变量的概率分布，所得信息是有限的；而若能描述多个变量的联合行为，则能够触及更深层的规律。从某种意义上说，联合分布为多维结构提供了整体框架，而边缘分布则描述了局部特征，并由此构成多变量概率分析的两个核心维度。

在深入讨论之前，有必要强调，联合分布与边缘分布之间的关系并非简单的“部分”与“整体”对照，而是构成理解多维不确定结构的一个逻辑体系。联合分布提供总体概率结构，而边缘分布通过求和或积分从高维结构中抽取低维信息。二者之间的相互联系构成了许多重要理论结果的基础，包括条件概率、相关结构、独立性判定、高维建模策略，以及现代生成模型中的分解方案。

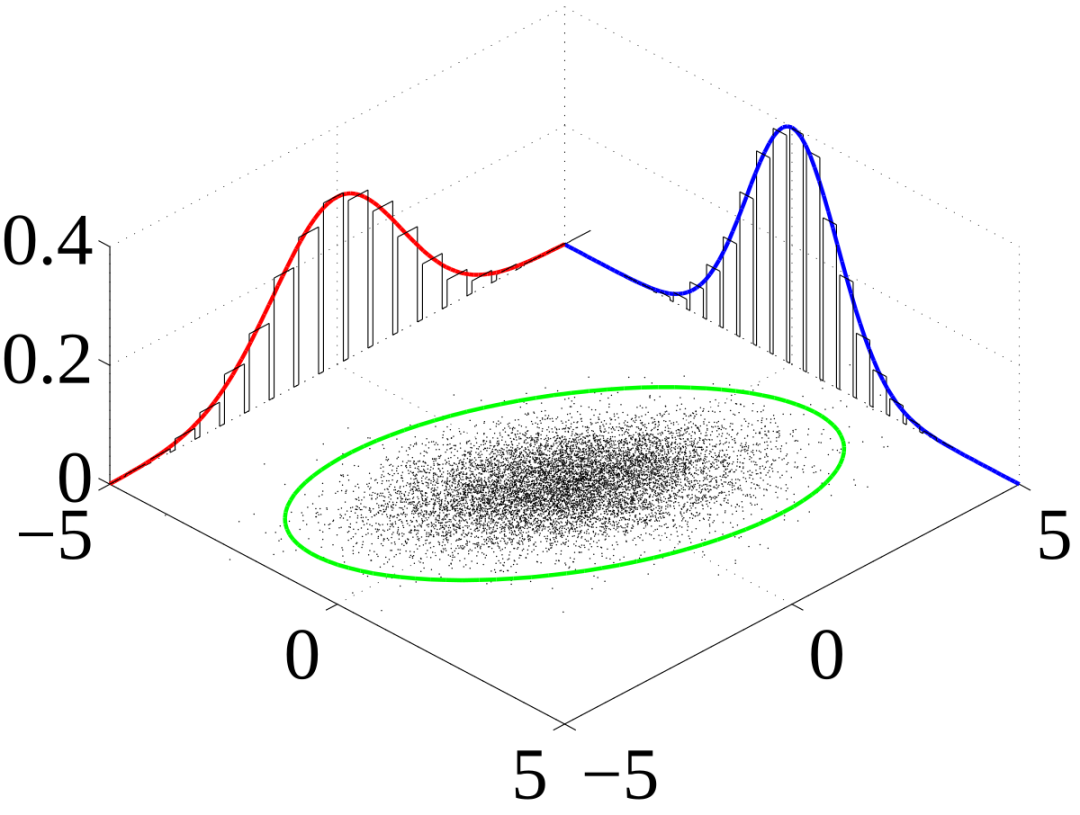
1 联合分布的概念与数学表述

联合分布不仅描述多个随机变量在某一概率空间上的联合行为，更揭示变量之间的依赖结构、相关关系乃至更一般的耦合形式。在多维概率模型中，没有联合分布就无法研究条件概率、独立性、相关性、协方差矩阵、Copula 结构、更一般的高维统计推断。因此，深入理解联合分布的定义、数学形式、性质与物理含义，是进入高维概率论与统计推断的必备前提。

1.1 联合分布的定义

（1）离散型随机变量的联合分布

设两个随机变量 X 与 Y 定义在同一个概率空间上，且分别取值于可数集合 S_X、S_Y。它们的联合分布函数（或联合概率质量函数）定义为：

p_{X,Y}(x, y) = P(X = x, Y = y)

这个函数为我们提供了这样一个问题的答案：

“X 和 Y 在同一次随机试验中分别取到某具体值 x 与 y 的概率是多少？”

例如，当 X 表示一个骰子的点数，Y 表示另一个骰子的点数时，联合分布给出了两次掷骰子后的点数组合的完整概率结构。

（2）连续型随机变量的联合分布密度

若 X 和 Y 为连续随机变量，我们通常不再直接讨论“取某精确值”的概率（因为在连续情形下该概率为零），而是讨论它们的联合概率密度函数（PDF）：

f_{X,Y}(x, y)

其含义是：

在小面积元素 dx dy 上，事件“X 落在 x 附近、Y 落在 y 附近”的概率近似为 f_{X,Y}(x, y) dx dy。

这体现了密度的本质：密度本身不是概率，但密度在小区域上的积分可以给出概率。

（3）联合分布函数（Joint CDF）

除了使用 PMF 或 PDF，联合分布还可由联合累积分布函数（CDF）来表达，其定义为：

F_{X,Y}(x, y) = P(X <= x, Y <= y)

CDF 不要求随机变量必须连续，可以覆盖离散、连续或混合型随机变量，是更一般的描述方式。

其性质包括：

• F_{X,Y}(x, y) >= 0
• 随 x、y 单调不减
• 边界极限：lim_{x->-∞} F_{X,Y}(x, y) = 0, lim_{x->+∞, y->+∞} F_{X,Y}(x, y) = 1

（4）多维扩展：n维联合分布

联合分布可自然扩展至 n 维随机向量 (X1, X2, ..., Xn)：

其联合 CDF 为：
F_{X}(x1, x2, ..., xn) = P(X1 <= x1, X2 <= x2, ..., Xn <= xn)

若有联合密度（并非总是有），则定义联合 PDF：
f_{X}(x1, x2, ..., xn)

这类 n 维联合密度不仅用于理论研究，也用于现代机器学习模型（如变分自编码器、分布模型）中构建高维数据分布，是人工智能领域的重要基础。

1.2 联合分布的性质

联合分布具有一系列基本且关键的数学性质，使其能够成为高维概率分析的核心工具。

（1）非负性

对于密度函数：f_{X,Y}(x, y) >= 0
对于离散分布：p_{X,Y}(x, y) >= 0

这是概率论的基本要求：概率不能为负，密度也必须保持非负，否则无法解释为积累概率的速率。

（2）归一化（Normalization）

联合分布必须满足“总概率为 1”，因此：

• 离散型：∑_{x∈S_X} ∑_{y∈S_Y} p_{X,Y}(x, y) = 1
• 连续型：∫_{-∞}^{∞} ∫_{-∞}^{∞} f_{X,Y}(x, y) dx dy = 1

在多维情况下，这对应 n 重积分：
∫ ... ∫ f_{X}(x1, ..., xn) dx1 ... dxn = 1

归一化保证了联合分布是规范的概率模型。

（3）导出边缘分布

联合分布是更高维的结构，它可以“投影”到任一维度得到边缘分布。

连续型：f_X(x) = ∫_{-∞}^{∞} f_{X,Y}(x, y) dy
离散型：p_X(x) = ∑_{y∈S_Y} p_{X,Y}(x, y)

这里的“积分”或“求和”本质上是将另一个变量“消去”。因此边缘分布包含较少信息，是联合分布的一种降维。

（4）由联合分布导出条件分布

联合分布是条件分布的基础。例如：
f_{Y|X}(y|x) = f_{X,Y}(x, y) / f_X(x)，若 f_X(x) > 0。

若 f_X(x)=0，则条件分布在该点无意义。条件分布不仅用于贝叶斯推断，还用于马尔可夫过程、信息论、方差分解等关键领域。

（5）变量独立性的判定依据

若两个变量独立，则联合分布可被分解为边缘分布的乘积：
f_{X,Y}(x, y) = f_X(x) f_Y(y)（连续型）
p_{X,Y}(x, y) = p_X(x) p_Y(y)（离散型）

这提供了判断独立性的充分必要条件。

1.3 联合分布的实际意义

联合分布不仅是数学概念，更是建模现实问题的关键工具。

（1）描述变量之间的依赖关系

现实世界中绝大多数随机变量都不是独立的，例如：

• 金融中股价、利率、波动率之间高度耦合；
• 物理测量中温度、压力、粒子能量往往相互依赖；
• 机器学习中多个特征同时影响预测结果。

联合分布描述的就是这种“多变量共变模式”。

（2）构建条件概率、协方差与相关性

协方差可以由联合密度得出：
Cov(X, Y) = ∫∫ (x - μ_X)(y - μ_Y) f_{X,Y}(x, y) dx dy

又如相关系数：
ρ_{XY} = Cov(X, Y) / (σ_X σ_Y)

这些量在统计学、物理学、机器学习中都是理解系统结构的关键指标。

（3）用于复杂概率模型的基础

若没有联合分布，就无法进行：

• 贝叶斯网络（Bayesian Networks）
• 马尔可夫随机场（MRF）
• 隐马尔可夫模型（HMM）
• 高斯混合模型（GMM）
• Copula模型（金融风险建模核心工具）
• 深度生成模型（VAE、Flow-based models）

联合分布提供了所有这些模型的共同底层结构。

（4）在真实系统中的意义

例如，金融中两个资产收益 X 与 Y 的联合分布可以衡量：

• 两资产是否呈尾部相关性？
• 投资组合风险是否被低估？

物理中多个测量量的联合分布可以揭示：

• 是否有隐含变量？
• 测量量之间的耦合关系是否强烈？
• 系统是否需要高维模型而非单变量模型？

因此，联合分布是分析复杂系统的最完整描述工具。

2 边缘分布的概念与数学表述

边缘分布是从联合分布中“投影”出的单变量概率结构。它描述单个随机变量自身的概率行为，不关心其他变量具体取什么值。边缘分布在统计学中用来研究单变量属性，是方差、期望、分布形状、分位数、峰度、偏度等常见统计量的基础。

2.1 边缘分布的定义

若 X 和 Y 拥有联合分布，则 X 的边缘分布定义为：
f_X(x) = ∫_{-∞}^{∞} f_{X,Y}(x, y) dy（连续）
p_X(x) = ∑_{y} p_{X,Y}(x, y)（离散）

（1）离散型边缘分布

这是在所有可能的 y 上求和，意味着我们“不关心 Y，只关心 X”。

例如，若 X、Y 表示两个设备的状态（故障/正常），则 p_X(故障) 表示设备 X 的故障概率，而不管另一台设备发生了什么。

（2）连续型边缘分布

这从几何上可直观解释为：
若 f_{X,Y}(x, y) 是 x-y 二维平面上的“概率密度地形图”， f_X(x) 则是将该地形对 y 方向进行“压缩”后的投影。

因此边缘分布反映的是变量自身的总体概率权重。

（3）高维情况的边缘分布

例如随机向量 (X1, X2, X3) 中 X1 的边缘分布：
f_{X1}(x1) = ∫_{-∞}^{∞} ∫_{-∞}^{∞} f_{X1,X2,X3}(x1, x2, x3) dx2 dx3

这个定义被广泛应用于生成模型、深度概率模型、贝叶斯推断。

2.2 边缘分布的性质

（1）非负性
f_X(x) >= 0，p_X(x) >= 0。
这是概率密度的基本特性。

（2）归一化
离散型：∑_{x} p_X(x) = 1
连续型：∫_{-∞}^{∞} f_X(x) dx = 1
边缘分布既然描述“单变量的全部概率”，当然必须归一化为 1。

（3）由联合分布导出（而反之不成立）

边缘分布总能由联合分布导出，但反之不成立。也就是说：
两个随机变量可能具有完全相同的边缘分布，但联合分布完全不同。

例如：

• 两变量独立时：f_{X,Y}(x, y) = f_X(x) f_Y(y)
• 两变量完美正相关时：即使 f_X 和 f_Y 是同样的分布，它们的联合分布是集中在 y=x 直线上。

因此边缘分布无法重建依赖信息。

2.3 边缘分布的应用

虽然边缘分布信息量少于联合分布，但它在很多实际应用中必不可少。

（1）用于描述单变量的统计特性

边缘分布用于计算：

• 均值 E[X]
• 方差 Var(X)
• 分位数
• 偏度、峰度
• 是否符合正态分布（例如构建 Q-Q 图时）

这些是最基础的统计量，广泛用于数据分析、统计推断、机器学习特征工程。

（2）用于机器学习模型中的特征建模

例如朴素贝叶斯分类器：

• 假设特征条件独立
• 则需要使用各特征的边缘分布或条件分布

在概率图模型中，经常需要对边缘分布进行推断（Marginal Inference），例如：

• 求 P(X1)
• 求 P(X1 | X3)

这些都是现代 AI 模型中的核心任务，深入的人工智能模型研究离不开对边缘概率的精确计算。

（3）用于风险管理与统计模拟

金融中常需要：

• 单一资产的收益分布
• 单一风险因子的波动结构
• 分位数（如 Value-at-Risk）

这些均由边缘分布给出。

（4）用于高维模型的降维与特征选择

在探索性数据分析（EDA）中，人们通常首先观察每个变量的边缘分布来判断变量是否：

• 偏态或对数正态
• 有重尾
• 是否需要对变量进行变换（如 Box-Cox、对数变换）
• 是否包含离群值

边缘分布是最直观的特征检查工具。

3 联合分布与边缘分布的本质差异

3.1 信息量与依赖关系

联合分布提供多变量的完整信息，包括变量间的依赖关系；而边缘分布只描述单变量的概率特性，失去了变量之间的依赖信息。

• 联合分布：包含 X 和 Y 的联合行为信息
• 边缘分布：仅包含 X 的整体概率信息

从信息理论的角度看，边缘分布是联合分布的降维表示，其信息量小于或等于联合分布。

3.2 条件概率与联合分布的关系

联合分布与条件分布密切相关：
f_{X,Y}(x, y) = f_{X|Y}(x|y) f_Y(y) = f_{Y|X}(y|x) f_X(x)

其中 f_X(x) 和 f_Y(y) 是边缘分布。联合分布可以分解为边缘分布与条件分布的乘积，但边缘分布无法单独重建联合分布的完整信息，除非假设变量独立。

3.3 变量独立性的判定

边缘分布在判断变量独立性中发挥重要作用：若 X 与 Y 独立，则
f_{X,Y}(x, y) = f_X(x) f_Y(y)

这一性质直接体现了联合分布与边缘分布之间的关系。联合分布能够揭示变量间的依赖模式，而边缘分布仅提供单变量概率，不足以判断变量间是否独立。

4 联合分布与边缘分布的计算方法

4.1 离散型变量的计算示例

假设有两个离散随机变量 X 和 Y，取值集合分别为 {0， 1}，联合概率分布如下表：

X\Y	0	1
0	0.1	0.4
1	0.2	0.3

边缘分布为：

• X 的边缘分布：p_X(0)=0.1+0.4=0.5， p_X(1)=0.2+0.3=0.5
• Y 的边缘分布：p_Y(0)=0.1+0.2=0.3， p_Y(1)=0.4+0.3=0.7

条件分布示例：
p_{X|Y}(0|0) = p_{X,Y}(0,0) / p_Y(0) = 0.1 / 0.3 ≈ 0.333

4.2 连续型变量的计算示例

设联合概率密度函数为
f_{X,Y}(x, y) = x + y， 0<=x<=1， 0<=y<=1
其他区域为 0。

边缘密度函数为：
f_X(x) = ∫_{0}^{1} (x+y) dy = x + 1/2， 0<=x<=1
f_Y(y) = ∫_{0}^{1} (x+y) dx = y + 1/2， 0<=y<=1

条件密度函数为：
f_{X|Y}(x|y) = f_{X,Y}(x, y) / f_Y(y) = (x+y) / (y + 1/2)， 0<=x<=1

通过这些示例可以清晰看到联合分布如何提供全面信息，边缘分布则为单变量概率提供简化表示。

5 联合分布与边缘分布在应用中的价值

5.1 数据分析与特征选择

在大数据分析中，联合分布用于识别变量间的复杂依赖模式，边缘分布则帮助快速了解单变量统计特性。通过联合分布与边缘分布的联合使用，可以在高维数据中高效进行特征选择、变量降维和关系分析。

5.2 风险管理与金融建模

联合分布在金融风险管理中用于模拟多资产组合的联合风险，而边缘分布则用于单资产的风险度量。通过联合分布计算条件风险指标，如条件尾部风险（Conditional Value-at-Risk， CVaR），能够获得更精确的风险评估。

5.3 物理系统与实验设计

在实验物理中，联合分布描述多个测量量在同一次实验中可能的值组合，边缘分布则帮助分析单个测量量的分布特性。联合分布在系统建模中是不可或缺的基础工具，边缘分布则便于数据可视化和初步统计分析。

5.4 机器学习与统计建模

在机器学习中，联合分布与边缘分布用于特征建模、概率图模型构建和生成模型设计。联合分布提供全局依赖信息，边缘分布可用于独立假设模型或特征单独评估。对于贝叶斯网络和马尔科夫随机场，联合分布是核心，而边缘分布则用于局部推断和边际概率计算。理解这些概念是进行有效数据分析和模型构建的前提。

6 总结

联合分布与边缘分布是概率论中多变量分析的核心概念。联合分布提供全面的多变量概率信息，揭示变量间依赖关系，并可导出条件分布和边缘分布。边缘分布通过积分或求和从联合分布获得单变量的概率分布，反映单变量整体特性，但失去变量间依赖信息。理解两者的区别和联系，对于数据分析、统计建模、风险评估、机器学习和实验设计都具有深远意义。联合分布是多变量分析的全景视图，而边缘分布是关注单变量行为的简化表达。两者结合使用，能够在复杂随机系统中提供精确的概率描述与分析手段。