差速底盘MPC轨迹跟踪：基于Simulink的横纵向联合控制仿真实现

两轮差速移动机器人（WMR）的轨迹跟踪控制是一个经典问题，需要同时兼顾纵向速度跟踪与横向路径跟踪。传统PID控制方法在应对这种多目标耦合任务时，往往难以协调。本文将探讨如何利用模型预测控制（MPC）这一先进控制算法，在Matlab/Simulink环境中实现对差速底盘横纵向轨迹的联合跟踪控制，并通过五种典型轨迹进行仿真验证。

本文项目采用Simulink搭建被控对象模型，使用Matlab代码编写MPC控制器，实现了无需第三方软件联合仿真的完整仿真流程。

!DAMO开发者矩阵

一、差速底盘运动学建模

控制算法的设计始于精确的模型。对于两轮差速底盘，其核心原理是通过左右轮的转速差实现转向。将车体坐标系下的运动转换至世界坐标系，可建立如下状态方程：

% 状态量：x位置、y位置、航向角θ、线速度v
% 控制量：左右轮转速差Δω
function dx = kinematicModel(~, x, u)
    L = 0.5; % 轮距
    v = x(4);
    theta = x(3);
    dx = [v * cos(theta);
          v * sin(theta);
          (u(1) - u(2)) / L; % 航向角变化率
          (u(1) + u(2)) / 2]; % 线速度变化率
end

该模型是MPC预测未来N步系统状态的基础，即根据当前的速度与方向，递推预测未来一段时间内的机器人轨迹。

!机器人运动学模型状态变量示意图

二、MPC控制器设计：增量式优化

为了确保控制量输出平滑，避免突变，本设计采用了控制增量作为优化变量，而非直接优化控制量本身。这种增量式MPC通过在目标函数中惩罚控制量的变化，使输出更平稳。

% MPC目标函数核心代码段（简化示意）
cost = 0;
for k = 1:N
    % 惩罚状态误差（跟踪精度）
    cost = cost + (X(k，：) - refTraj(k，：)) * Q * (X(k，：) - refTraj(k，：))';
    if k < N
        % 惩罚控制增量（输出平滑度）
        cost = cost + deltaU(k，：) * R * deltaU(k，：)';
    end
end

其中，Q和R分别为状态误差和控制增量的权重矩阵。调整R矩阵的权重可以有效调节系统的“激进”程度：权重越大，控制动作越温和，但响应速度可能下降；反之，跟踪可能更迅速，但控制输出波动更大。这涉及到经典的算法优化与权衡问题。

三、仿真验证：五种轨迹生成

为全面验证控制器性能，项目预设了五种参考轨迹进行测试，包括不同车速的圆形轨迹、直线轨迹以及双移线轨迹。

% 示例：双移线轨迹（Double Lane Change）生成函数
function ref = generateDoubleLane(v)
    t = 0:0.1:20;
    ref = [v * t';
           3.5 * sin(0.4 * t)';
           zeros(length(t), 1); % 航向角参考（简化）
           v * ones(length(t), 1)]; % 速度参考
end

• 圆形轨迹：主要考验控制器的横向路径跟踪能力，通过改变半径和车速组合测试不同工况。
• 直线轨迹：看似简单，但在高速下维持精确航向，需要MPC对左右轮速差进行极其精细的协调。
• 双移线轨迹：模拟“蛇形”绕桩，对控制器的动态响应和超调抑制能力提出较高要求。

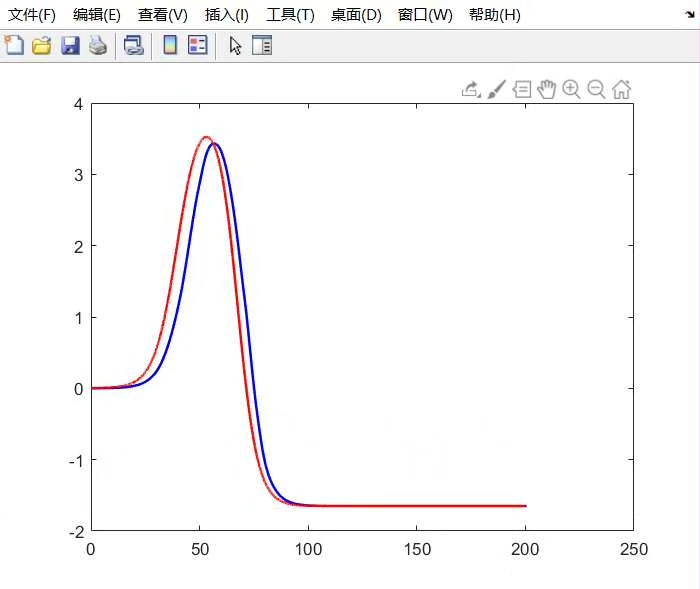
四、Simulink模型搭建要点

!Simulink模型中的MPC控制器S函数模块

在Simulink中，MPC控制器通常通过S-Function模块集成。一个关键配置是采样时间与预测步长的匹配。在本仿真中，采样周期设置为100ms，预测步长为10步，这意味着控制器每次都在优化未来1秒内的系统行为。经验表明，预测时域过长（如超过1.5秒）可能因模型误差累积而导致优化问题发散。

五、仿真结果与可视化分析

通过运行仿真，可以获取实际轨迹与参考轨迹的数据。项目内置了数据对比与绘图脚本，可一键生成分析图表。

% 轨迹对比可视化代码
figure('Position', [200 200 800 600])
hold on;
plot(actualX, actualY, 'LineWidth', 2);
plot(refX, refY, '--r', 'LineWidth', 1.5);
legend('实际轨迹', '参考轨迹', 'Location', 'best');
xlabel('X位置 (m)'); ylabel('Y位置 (m)');
title('双移线轨迹跟踪效果对比');
grid on;
exportgraphics(gcf, 'result.png', 'Resolution', 300); % 导出高清图片

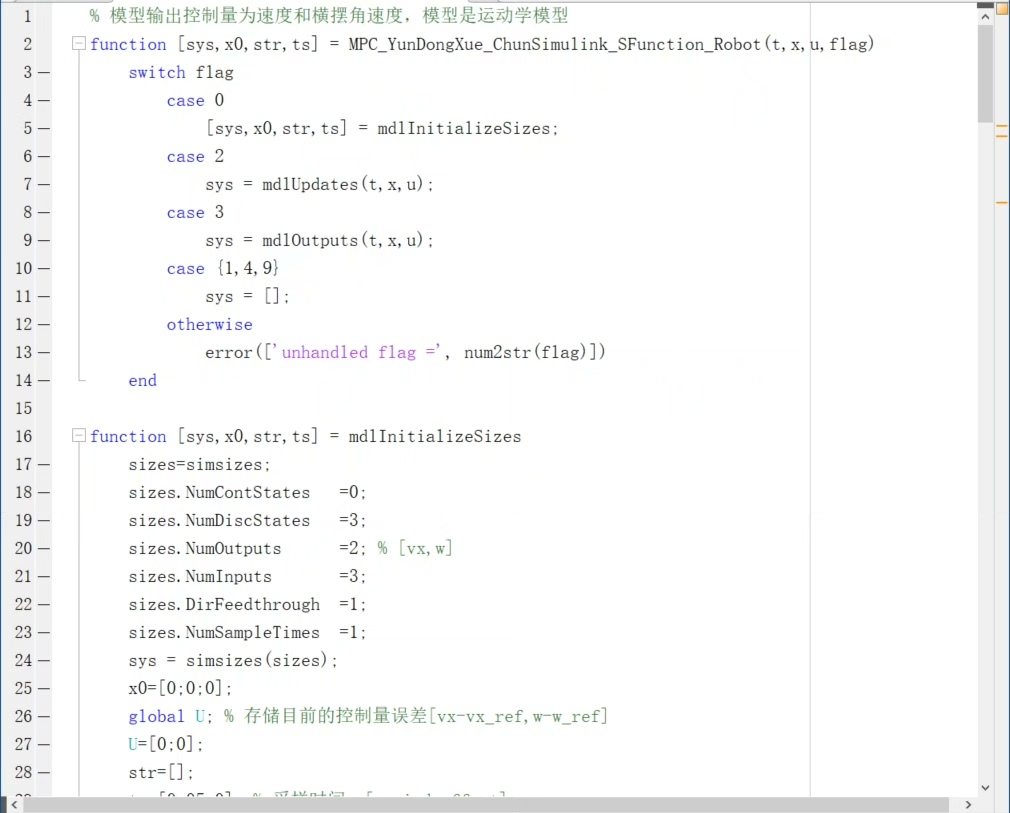
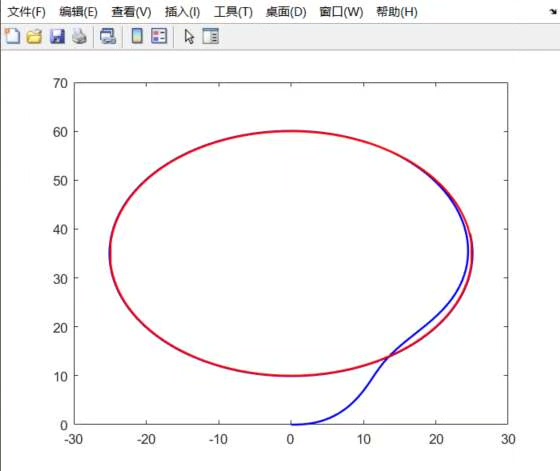
!轨迹跟踪效果对比图

!速度跟踪效果曲线图

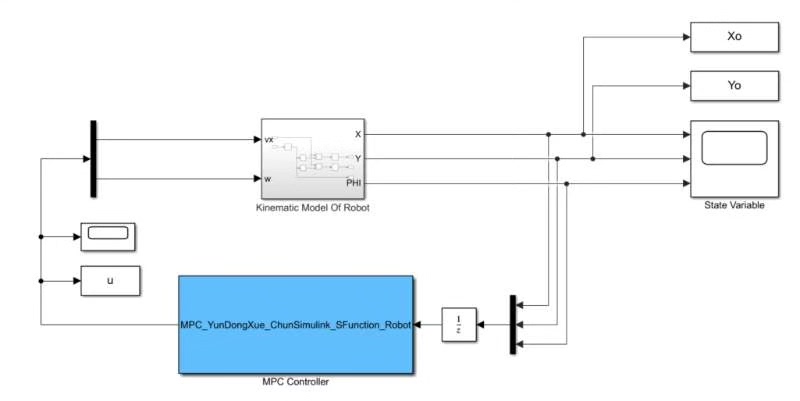
仿真结果表明：

1. 圆形轨迹跟踪：横向位置误差可稳定在0.1米以内。
2. 双移线轨迹跟踪：在轨迹曲率突变点（转向点）会出现瞬时最大约0.2米的误差，但控制器能快速收敛修正。
3. 速度跟踪：全程速度跟踪误差保持在±0.05 m/s的范围内，体现了良好的纵向控制性能。

!更多仿真结果可视化图表

六、关键配置与调优建议

1. 雅可比矩阵计算：在构建MPC预测模型时，推荐使用数值差分法实时计算雅可比矩阵。使用符号计算虽然精确，但会大幅增加计算负担，影响实时性。
2. 控制量约束：设置电机转速或转矩约束时，建议留有约10%的余量。这能为优化求解器提供缓冲空间，避免因在约束边界来回震荡而导致求解失败。
3. 初始状态：若机器人的初始位姿与参考轨迹的起点偏差过大，MPC可能无法有效收敛。在实际应用中，可考虑结合“预瞄”或初始对准策略来改善。
4. 权重调整：Q和R矩阵的调参是核心。可遵循从单一轨迹（如直线）开始，初步调整使系统稳定，再在复杂轨迹（如双移线）上微调以平衡响应速度与平滑性的步骤。这个过程本身是人工智能与控制领域的一个实践结合点。

本文提供的完整仿真模型代码结构规范，关键部分均有详细注释，并附有相关参考文献，可供进一步研究与开发。