C++递归编程深度解析：从阶乘、斐波那契到循环展开优化

递归（Recursion）是一种强大的编程范式，指函数或模板在其定义中直接或间接地调用自身。其核心思想是将一个复杂的原问题，分解为多个结构相同但规模更小的子问题，直至分解到可直接求解的基本情况。

递归的核心特征

• 自引用性：函数或模板的定义中包含对自身的调用。
• 问题分解：将大规模问题拆解为同类型的子问题。
• 终止条件：必须存在明确的、可使递归停止的边界条件。
• 收敛性：每一次递归调用都必须使问题规模向终止条件靠近。

递归的数学基础

递归在数学中对应递归定义，例如：

• 阶乘：n! = n × (n-1)!，其中 0! = 1
• 斐波那契数列：F(n) = F(n-1) + F(n-2)，其中 F(0) = 0, F(1) = 1

其基本语法形式如下：

返回类型 函数名(参数列表) {
    // 终止条件（边界条件）
    if (终止条件) {
        return 终止值;
    }
    // 递归调用：函数名(修改后的参数)
    return 函数名(修改后的参数);
}

示例代码详解

示例1：计算阶乘（经典递归）

// 计算 n! = n × (n-1) × (n-2) × ... × 1
int factorial(int n) {
    // 终止条件：0! = 1, 1! = 1
    if (n == 0 || n == 1) {
        return 1;
    }
    // 递归关系：n! = n × (n-1)!
    return n * factorial(n - 1);
}

// 调用示例：factorial(5)
// factorial(5) = 5 × factorial(4)
//              = 5 × (4 × factorial(3))
//              = 5 × (4 × (3 × factorial(2)))
//              = 5 × (4 × (3 × (2 × factorial(1))))
//              = 5 × (4 × (3 × (2 × 1)))
//              = 120

执行过程可视化：

factorial(5)
  └─> 5 * factorial(4)
        └─> 4 * factorial(3)
              └─> 3 * factorial(2)
                    └─> 2 * factorial(1)
                          └─> 1  (终止条件)

示例2：编译期模板递归（循环展开）

template<int N>
struct LoopUnroll {
    template<typename F>
    static void run(F func) {
        LoopUnroll<N - 1>::run(func); // 递归处理前N-1次
        func(N - 1); // 执行第N次（索引N-1）
    }
};

// 终止条件：N=0时停止递归
template<>
struct LoopUnroll<0> {
    template<typename F>
    static void run(F func) {
        // 空实现，结束递归
    }
};

当调用 LoopUnroll<4>::run(func) 时，展开过程如下：

LoopUnroll<4>::run(func)
  └─> LoopUnroll<3>::run(func)  // 递归调用
        └─> LoopUnroll<2>::run(func)  // 递归调用
              └─> LoopUnroll<1>::run(func)  // 递归调用
                    └─> LoopUnroll<0>::run(func)  // 终止条件，什么都不做
                    └─> func(0)  // 执行
              └─> func(1)  // 执行
        └─> func(2)  // 执行
  └─> func(3)  // 执行

此技巧常用于编译期元编程，实现循环展开以提升运行时性能。

示例3：斐波那契数列

// 斐波那契数列：F(0)=0, F(1)=1, F(n)=F(n-1)+F(n-2)
int fibonacci(int n) {
    // 终止条件
    if (n == 0) return 0;
    if (n == 1) return 1;
    // 递归关系：F(n) = F(n-1) + F(n-2)
    return fibonacci(n - 1) + fibonacci(n - 2);
}
// fibonacci(5) 的计算过程：
// F(5) = F(4) + F(3)
//      = (F(3) + F(2)) + (F(2) + F(1))
//      = ((F(2) + F(1)) + (F(1) + F(0))) + ((F(1) + F(0)) + 1)
//      = ... 最终得到 5

注意：此朴素递归实现存在大量的重复计算问题。在实际应用中，常使用带备忘录的递归或迭代法进行优化，这也是动态规划算法的基本思想之一。

递归与循环的对比与选择

递归和循环（迭代）在逻辑上可以相互转换。

1. 相互转换示例

// 用循环计算阶乘
int factorial_loop(int n) {
    int result = 1;
    for (int i = 1; i <= n; i++) {
        result *= i;
    }
    return result;
}

// 用递归计算阶乘
int factorial_recursive(int n) {
    if (n <= 1) return 1;
    return n * factorial_recursive(n - 1);
}

2. 递归的优缺点分析

优点：

• 代码简洁：对于树形结构、分治算法等问题，递归代码更贴近问题本身的数学定义，逻辑清晰。
• 易于理解：对于符合递归定义的问题（如文件树遍历），递归思维更直观。

缺点：

• 栈空间开销：每次递归调用都会在调用栈上增加一层，深度递归可能导致栈溢出。
• 可能的性能问题：存在重复计算的递归（如朴素斐波那契）效率低下。
• 调试难度：递归调用链较长时，跟踪执行状态比循环更复杂。

3. 如何选择：递归还是循环？

选择的关键在于问题的本质和上下文。

• 优先选择递归的场景：问题的定义本身就是递归的（如树/图的遍历、回溯、分治），或者使用递归能使代码极其清晰易懂。
• 优先选择循环的场景：性能要求苛刻，需要避免函数调用开销和栈溢出风险；问题本身更适合用线性步骤描述。

为了更直观地展示选择逻辑，可以参考以下决策图：

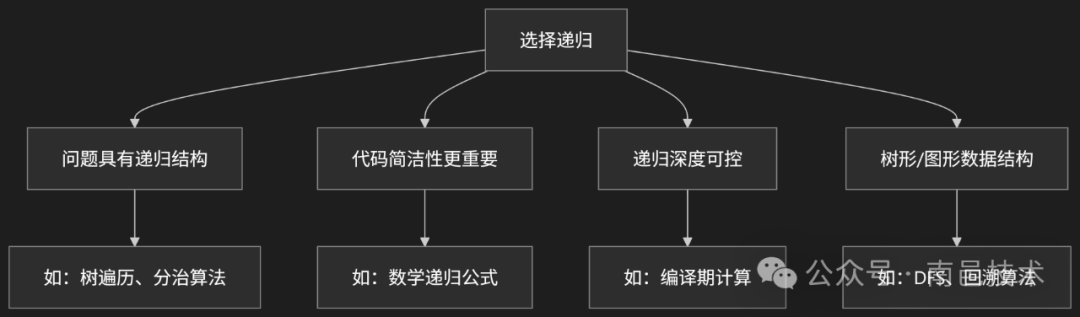
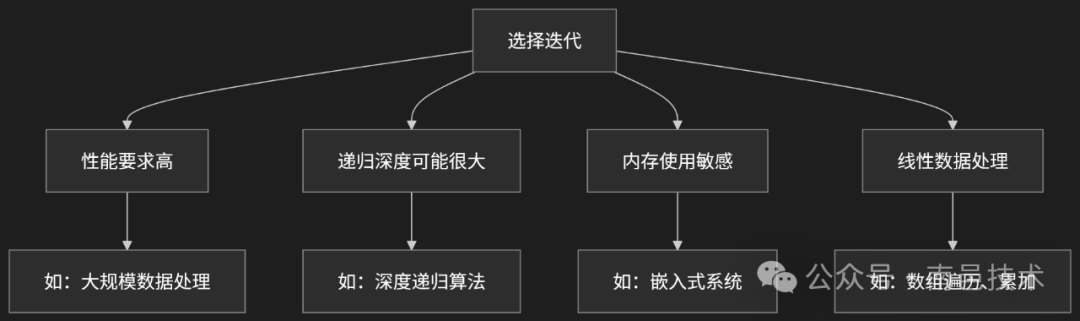
总结

递归是一种通过自我调用来分解问题的核心编程技术。它不仅有着坚实的数学基础，在C++等语言中还能优雅地应用于编译期计算与优化（如模板元编程实现循环展开）。深入理解递归的执行机制、优缺点及适用场景，是掌握高级算法设计与编写高效、清晰代码的关键一步。在实际开发中，应灵活权衡递归与迭代，根据具体问题选择最合适的工具。