2025年12月,南京发生大规模卫星导航信号异常,主流地图软件集体失灵,定位出现严重漂移。技术分析报告指出,其核心原因是GNSS卫星信号(含北斗、GPS)受到临时干扰压制。这一事件揭示了我们日常依赖的导航系统背后,隐藏着一套精密复杂的数学模型。
本文将从该事件切入,深入探讨卫星导航系统中的数学建模原理,解析“定位”这一功能背后蕴含的数学智慧。
定位问题的本质:空间几何与方程求解
三边测量法的基本原理
卫星导航定位的核心思想源于三边测量法(Trilateration)。其基本原理是:在二维平面中,若已知三个点的坐标以及待测点到这三点的距离,便可唯一确定待测点的位置。
设三个已知点(锚节点)的坐标为 ((x_1, y_1)), ((x_2, y_2)), ((x_3, y_3)),待测点坐标为 ((x, y)),到三个锚节点的距离分别为 (d_1), (d_2), (d_3)。根据勾股定理,可建立方程组:
[
\begin{cases}
(x - x_1)^2 + (y - y_1)^2 = d_1^2 \
(x - x_2)^2 + (y - y_2)^2 = d_2^2 \
(x - x_3)^2 + (y - y_3)^2 = d_3^2
\end{cases}
]
从几何角度看,每个方程代表以锚节点为圆心、对应距离为半径的圆,三个圆的交点即为待测点位置。理解这一基础几何原理,是掌握更复杂算法与数据结构应用的前提。
从二维到三维:卫星定位的空间模型
将上述原理推广至三维空间,卫星导航系统以高空卫星作为“锚节点”。每颗卫星向地面广播其精确的空间坐标 ((X_i, Y_i, Z_i)),接收机通过测量信号传播时间来计算距离 (d_i)。
设接收机位置坐标为 ((X, Y, Z)),则有:
[
(X - X_i)^2 + (Y - Y_i)^2 + (Z - Z_i)^2 = d_i^2
]
理论上,三颗卫星可确定三维空间中的一个点。然而,实际工程远比理论复杂,这也正是导航数学建模的精妙之处。
伪距测量:时间与距离的转换
伪距的定义
卫星导航采用时间测距法:卫星发射信号时附带精确时间戳 (t{sv}),接收机记录接收时间 (t{rx}),通过时间差乘以光速 (c) 计算距离。
[
\rho = c \cdot (t{rx} - t{sv})
]
其中,光速 (c \approx 3 \times 10^8 m/s)。
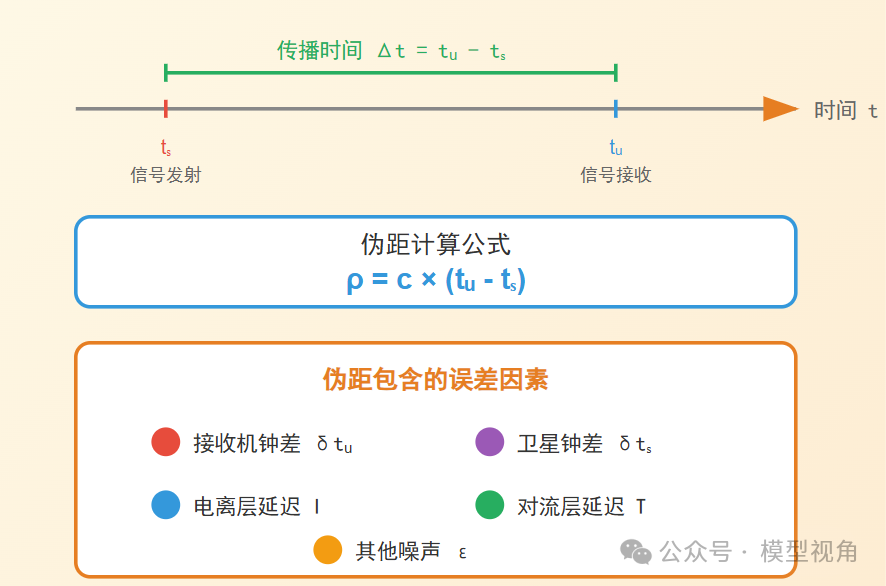
然而,这样计算出的距离并非真实几何距离。由于卫星时钟、接收机时钟均存在钟差,且信号穿过大气层会产生延迟,因此测得的距离包含多种误差,被称为伪距。
伪距观测方程
完整的伪距观测方程需综合考虑各项误差:
[
\rho = \rho_{geo} + c \cdot (\delta t_r - \delta t_s) + I + T + \epsilon
]
其中:
- (\rho_{geo}):真实几何距离
- (\delta t_r):接收机钟差
- (\delta t_s):卫星钟差
- (I):电离层延迟
- (T):对流层延迟
- (\epsilon):其他测量噪声
为什么需要四颗卫星?
这是卫星导航中最常见的问题之一,答案隐藏在未知数的数量中。
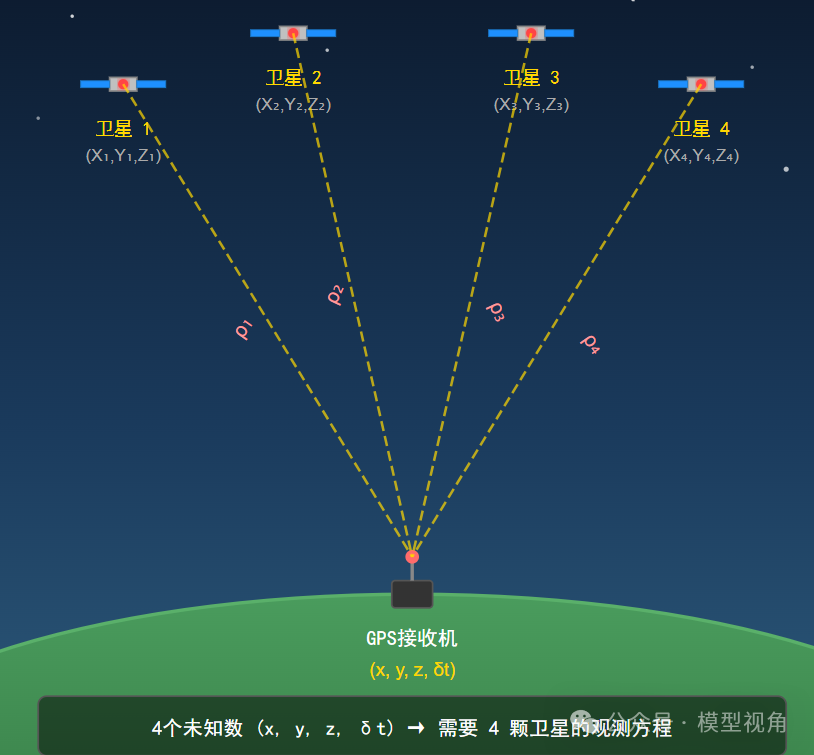
待求解的未知量包括:
- 接收机三维坐标 (X, Y, Z)(3个未知数)
- 接收机钟差 (\delta t_r)(1个未知数)
共计4个未知数。根据线性代数原理,求解4个未知数至少需要4个独立方程,因此至少需要观测4颗卫星。
设第 (i) 颗卫星坐标为 ((X_i, Y_i, Z_i)),伪距观测值为 (\rho_i),则可建立方程组:
[
\rho_i = \sqrt{(X - X_i)^2 + (Y - Y_i)^2 + (Z - Z_i)^2} + c \cdot \delta t_r + \epsilon_i, \quad i=1,2,3,4
]
非线性方程的线性化
观察上述伪距方程,因其包含平方根运算,属于非线性方程组,无法直接求解。工程实践中,通常采用泰勒级数展开进行线性化。
线性化过程
假设接收机的概略位置为 ((X_0, Y_0, Z_0)),真实位置为 ((X, Y, Z)),定义位置改正量 ((\delta X, \delta Y, \delta Z)):
[
X = X_0 + \delta X, \quad Y = Y_0 + \delta Y, \quad Z = Z_0 + \delta Z
]
将伪距方程在概略位置处进行一阶泰勒展开:
[
\rhoi \approx \rho{i0} + \frac{X_0 - Xi}{\rho{i0}} \delta X + \frac{Y_0 - Yi}{\rho{i0}} \delta Y + \frac{Z_0 - Zi}{\rho{i0}} \delta Z + c \cdot \delta t_r
]
其中,(\rho_{i0}) 为根据概略位置计算的理论距离。
矩阵形式与最小二乘解
将线性化方程组写成矩阵形式:
[
\mathbf{y} = \mathbf{A} \mathbf{x} + \mathbf{v}
]
其中:
- (\mathbf{y}):观测值与计算值之差组成的向量
- (\mathbf{A}):设计矩阵(由偏导数组成)
- (\mathbf{x} = [\delta X, \delta Y, \delta Z, c \cdot \delta t_r]^T):待求参数向量
- (\mathbf{v}):残差向量
当观测卫星数 (n > 4) 时,方程组为超定方程组,采用最小二乘法求解:
[
\hat{\mathbf{x}} = (\mathbf{A}^T \mathbf{A})^{-1} \mathbf{A}^T \mathbf{y}
]
通过迭代计算,不断更新概略位置,直至位置改正量小于设定阈值,即得到最终定位结果。
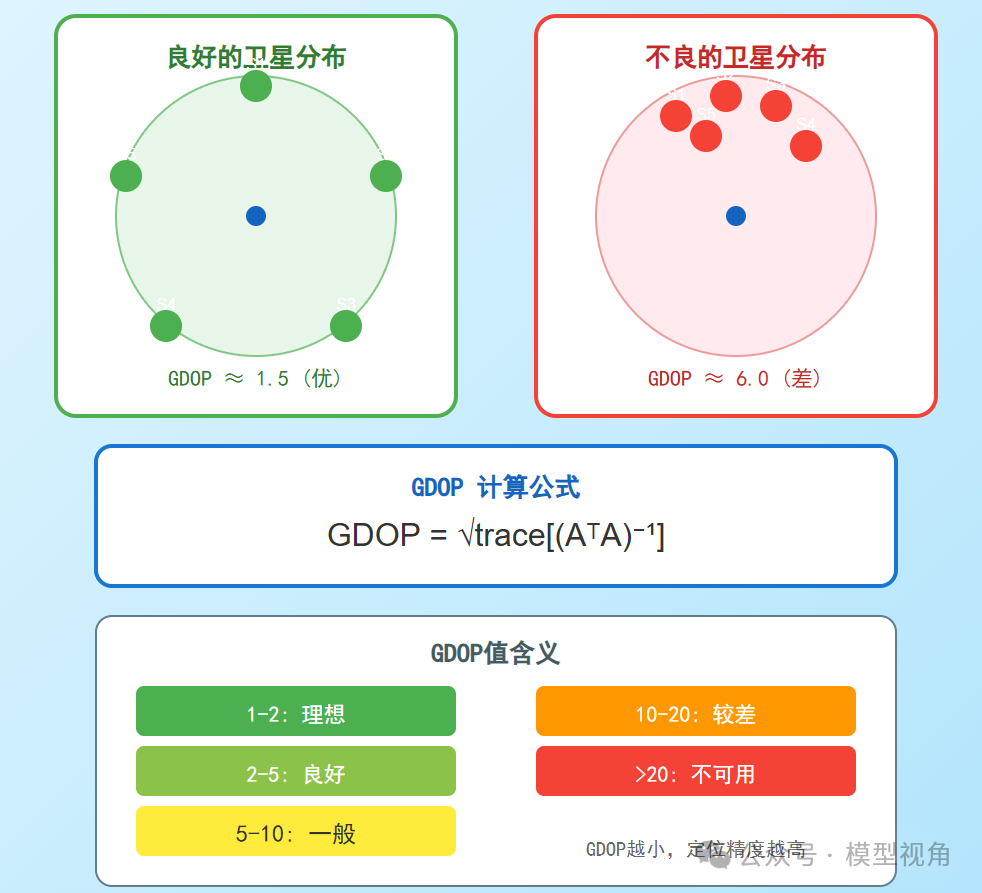
误差分析与精度因子
几何精度因子(GDOP)
即使方程求解正确,定位精度仍受卫星几何分布的影响。几何精度因子(Geometric Dilution of Precision, GDOP) 用于量化这种影响:
[
GDOP = \sqrt{\text{tr}((\mathbf{A}^T \mathbf{A})^{-1})}
]
GDOP值越小,表明卫星在空间分布越均匀、几何构型越好,定位精度越高。反之,若卫星集中在天空某一区域,GDOP值增大,定位精度将显著下降。
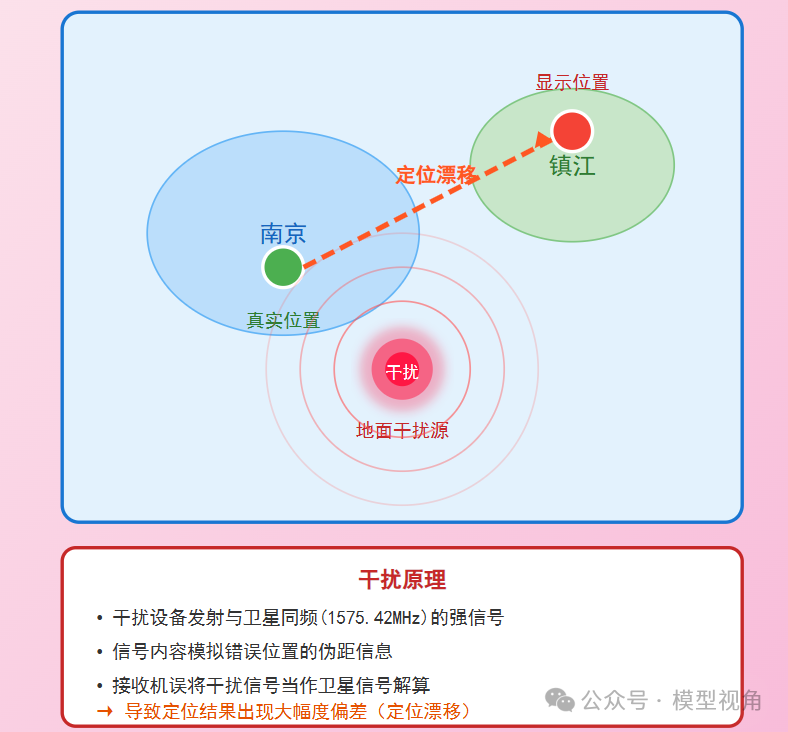
信号干扰的数学本质
回到南京导航信号异常事件。当地面发射与卫星信号同频的强干扰信号时,接收机会接收到错误的伪距信息。假设干扰源模拟镇江附近的坐标,则伪距观测方程变为:
[
\rho{干扰} \approx \rho{geo_镇江} + \cdots
]
接收机误将干扰信号当作真实卫星信号,代入错误的伪距值进行解算,自然得出错误的定位结果。这正是南京市民定位“漂移”至镇江等地的数学原因,也深刻揭示了网络安全与信号防护在关键基础设施中的重要性。
载波相位测量:追求毫米级精度
伪距测量精度受限于测距码的码元宽度。以GPS的C/A码为例,其码元宽度约300米,即使精确到1%,定位精度也只能达到米级。
为实现更高精度定位,需利用载波信号进行测距。GPS的L1载波波长仅约19厘米,若能分辨1%的相位差,理论精度可达毫米级。
载波相位观测方程为:
[
\Phi = \frac{\rho}{\lambda} + N + \epsilon_{\Phi}
]
其中,(\lambda) 为载波波长,(N) 为整周模糊度——这是载波相位测量的核心难题。由于接收机只能测量不足一个周期的相位差,信号传播的整周数需通过特定算法确定。
南京导航信号异常事件提醒我们,卫星导航虽已成熟应用,但其本质仍是对微弱电磁信号的精密测量与数学解算。正如南京卫星应用行业协会所指出,北斗与GPS民用频段的兼容设计具有战略意义,而军用频段采用的“全数字抗干扰技术”和“自适应智能滤波算法”,则是融合了更高阶数学理论与工程实践的结晶,其背后的安全防护机制值得深入研究。