最小二乘法平差原理：从测量误差处理到现代数据分析的数学核心

在测量学与地理信息科学中，一个常见的基础问题是：当观测值的数量多于未知参数时，如何从这些不可避免地带有误差的数据中，获取最可靠、最合理的解？最小二乘法平差 正是解决这一核心问题的数学利器。

一、什么是平差？

简单来说，平差就是处理各观测值之间矛盾、消除测量误差，从而求解未知量的最佳估值，并评估结果精度的理论与方法。

我们可以通过一个简单的例子来理解：测量一个三角形的三个内角。理论上，其内角和应为180度。但在实际测量中，由于仪器、环境等因素，三个角的测量值之和可能是180.5度或179.8度。平差的目的，就是通过数学方法，合理地调整各个观测值（即分配“改正数”），以消除这个“和不等于180度”的矛盾。

二、最小二乘法的基本原理

最小二乘法的核心思想非常直观且强大：使所有观测值的改正数（或称残差）的平方和达到最小。

其数学目标可以表述为：

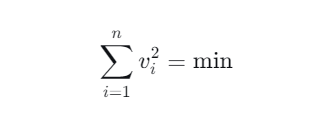
其中，( v_i ) 代表第 ( i ) 个观测值的改正数。这一准则由法国数学家勒让德于1806年明确发表，而高斯声称更早使用了该方法。因其在数学上的严谨性与实践中的卓越效果，最小二乘原理成为了测量平差乃至许多其他数据处理领域的基石。

三、最小二乘平差的主要方法

根据建立数学模型方式的不同，传统的最小二乘平差主要分为两类。

3.1 间接平差（参数平差）

间接平差选择一组与观测值有函数关系的独立未知量作为参数，通过建立观测值与这些参数之间的函数模型，并依据最小二乘准则来求解参数的最佳估值。

其函数模型的一般形式为：

L = BX + d

式中，L 是观测值向量，X 是待求的未知参数向量，B 是系数矩阵，d 是常数向量。

3.2 条件平差

条件平差不直接求解未知参数，而是以所有观测值的改正数本身作为未知量。这些改正数必须满足由观测值之间几何或物理关系构成的条件方程，并在满足所有条件的前提下，使改正数的平方和最小。

其函数模型的一般形式为：

AV + W = 0

式中，A 是条件方程的系数矩阵，V 是观测值的改正数向量，W 是闭合差向量。

四、现代最小二乘平差的应用

随着计算技术的发展，最小二乘法已从传统的测量学扩展到众多科学与工程领域，成为数据分析与参数估计的通用框架。

• 卫星定位（如GPS）：解算接收机位置、速度及钟差等关键参数的核心算法。
• 摄影测量与三维重建：从多张二维影像中高精度恢复物体三维结构。
• 工程变形监测：用于分析大坝、桥梁、高层建筑等结构的微小形变。
• 工业精密测量：在机械加工、航空航天等领域进行质量控制与校准。
• 机器学习与数据拟合：作为线性回归、曲线拟合等算法的理论基础，用于从数据中学习模型。

总结

最小二乘法平差不仅是一套解决具体测量问题的成熟方法论，更体现了通过优化从噪声数据中逼近真理的科学思想。从基础的三角形角度平差到复杂的全球卫星导航系统解算，其原理始终发挥着关键作用。在大数据与人工智能时代，这种寻求“最优解”的数学艺术，继续在更广阔的数据科学、机器学习等领域展现着持久的生命力。