随机森林分类算法详解：从原理到实战，如何处理非线性与不平衡数据？

在机器学习的分类任务中，我们给定一个训练样本集，其中每个样本由特征向量和对应的类别标签组成。我们的目标，是在未见过的样本上给出尽可能准确的类别预测，同时提供可靠的类别概率估计。

随机森林正是解决这类问题的有力工具。它是一种基于 Bagging 自助采样集成 的决策树集成分类器。其核心策略可概括为“样本重采样 + 特征子抽样 + 全生长决策树”。通过这种方式，它能在不显著增加模型偏差的同时，大幅降低方差，从而有效提升模型的泛化性能与鲁棒性。

核心原理

决策树（分类树CART）与分裂准则

决策树通过递归地划分特征空间来构建模型，其目标是让每个叶节点内的样本尽可能“纯净”。这个“不纯度”通常使用以下指标来衡量：

• 基尼系数
• 熵
• 误分类率

其中， 表示当前节点， 为该节点中类别 的相对频率。

在实际应用中，分类树大多使用基尼系数或熵。以二分类问题为例，假设正类的样本比例为 ，则基尼系数可以表示为 。当 时，基尼系数达到最大值0.5，这意味着此时节点内样本的类别分布最为混乱，不纯度最高。

模型在寻找最优分裂点时，会在所有候选划分上，计算不纯度的下降量，并选择使下降量最大的划分：

ΔI(s, t) = I(t) - (N_left/N_t) * I(t_left) - (N_right/N_t) * I(t_right)

其中， 为父节点的不纯度， 为父节点的样本数， 和 分别为左右子节点的样本数， 和 为左右子节点。

这等价于最小化左右子节点的加权不纯度：

(N_left/N_t) * I(t_left) + (N_right/N_t) * I(t_right)

• 对于连续型特征，常用的分裂方式是选择一个阈值，例如 特征 <= 阈值 与 特征 > 阈值。
• 树的生长终止条件通常包括：达到预设的最大深度、叶节点包含的最小样本数不足、或者继续分裂无法带来足够的不纯度下降等。

完成训练后，分类树的预测方式非常简单：对于一个新的样本，将其送入树中，最终落入哪个叶节点，就以该叶节点中占比最多的类别作为预测结果，或者用叶节点内各类别的频率来估计类别概率。

Bagging：降低方差的核心策略

如果单个基学习器（例如一棵充分生长的决策树）本身具有较高的方差，那么它的预测可能很不稳定。Bagging 通过引入 样本随机性 来解决这个问题。

具体做法是：对原始训练集进行多次 Bootstrap 重采样（即有放回抽样），每次采样后得到一个子数据集，并在其上独立训练一个基模型。最终，通过集成所有基模型的预测结果（分类问题采用投票，回归问题采用平均）来得到最终预测。

假设我们有 棵树，每棵树的预测为 ，那么 Bagging 分类器的投票结果可以表示为：

C_bag(x) = argmax_{c} Σ_{b=1}^{B} I(C_b(x) = c)

其输出的概率估计（针对多分类）可以写为：

P_bag(y=c|x) = (1/B) Σ_{b=1}^{B} P_b(y=c|x)

其中， 是第 棵树在样本 最终落入的叶节点内，类别 的相对频率。

Bagging 的核心作用在于降低方差。假设单个基学习器的预测方差为 ，且任意两个基学习器预测结果之间的相关系数为 。那么，当我们平均 个这样的学习器时，集成的方差可以近似为：

ρ * σ^2 + (1-ρ)/B * σ^2

• 当树的数量 趋近于无穷大时，方差会收敛到 ，这个下界由树间的相关性 决定。
• 因此，降低基学习器之间的相关性是提升集成效果的关键。

随机森林：双重随机性

随机森林在 Bagging 的基础上，引入了 特征层面的随机性。具体而言，在训练每棵决策树的每个节点进行分裂时，算法不再从全部特征中挑选最佳分裂点，而是从一个随机选取的特征子集（通常大小为 ， 为特征总数）中进行选择。

这一策略进一步降低了树与树之间的相关性 ，从而能够更大幅度地降低整体模型的方差，提升泛化能力。

• 常用设置：对于分类任务，sklearn 中默认的 值为 sqrt(n_features)。
• 每棵树通常会被允许完全生长（即设置较小的 min_samples_leaf），以保持较低的偏差。

Breiman 在 2001 年提出了随机森林的“边际函数”概念，用于理论分析其泛化性能。泛化误差的上界与两个关键因素有关：单棵树的“强度” 和树间的平均相关性 。理想的情况是，每棵树都尽可能“强”（预测准确），同时树与树之间尽可能“独立”（相关性低）。随机特征子抽样正是通过降低 来优化这个上界的。

OOB估计：内置的验证工具

由于随机森林采用 Bootstrap 采样，在构建每棵树时，平均约有 37% 的原始训练样本不会被抽到。这部分未被抽到的样本，就称为该树的“袋外样本”。

对于一个训练样本 ，我们可以收集所有那些 在训练时未使用到 的树的预测，并用这些树的投票结果来预测 的类别。这样，我们就为每个训练样本都得到了一个“袋外预测”，进而可以计算出模型的袋外误差。

OOB 估计 是一种非常实用的工程技巧，它能在不额外划分验证集的情况下，对模型的泛化误差做出相当可靠的估计，其结果通常与留出法或交叉验证的结果相近。

特征重要性：MDI 与置换重要性

理解哪些特征对模型预测贡献最大，对于模型解释至关重要。随机森林提供了两种主要的特征重要性评估方法：

1. MDI：基于不纯度下降的重要性。
   特征 的重要性，等于在所有树的所有节点上，当 被选为分裂特征时所带来的不纯度下降的总和，并按节点样本数加权平均。
   其优点是计算高效；局限性在于可能对取值类别多的高基数特征，或存在强相关性的特征群产生偏差。

2. 置换重要性：这是一种模型无关的方法。
   具体操作是：在验证集或测试集上，随机打乱特征 的取值顺序，然后观察模型性能指标（如准确率、F1分数）的下降幅度。下降越多，说明该特征越重要。
   其优点是与最终的评价指标直接挂钩，解释性更强；缺点是计算成本较高，且对于强相关的特征，其重要性可能会被“分摊”或产生“替代”效应。

概率输出与校准

随机森林可以直接输出类别概率。对于样本 ，第 棵树会将其划分到某个叶节点 ，该叶节点中类别 的频率即为 。那么，随机森林对类别 的最终概率估计，就是所有树的叶节点类频率的平均值：

P_RF(y=c|x) = (1/B) Σ_{b=1}^{B} p_{t_b(x)}(y=c)

由于这个概率估计来源于叶节点内有限样本的统计，其结果可能比较离散。在对概率质量要求极高的任务中（如风控、医疗诊断），可以进一步使用 Platt Scaling 或 Isotonic Regression 等校准方法对输出概率进行后处理。

计算复杂度与可扩展性

• 训练复杂度：单棵决策树的训练复杂度期望约为 。随机森林包含 棵树，且树与树之间的训练可以完全并行，因此总复杂度约为 。
• 预测复杂度：对于单个样本，需要遍历 棵树，因此预测复杂度为 。

得益于其高度的可并行性，随机森林能够有效利用多核CPU或分布式计算资源，处理大规模数据集。

完整案例

接下来，我们通过一个完整的代码案例，来展示随机森林如何应对一个具有挑战性的场景：一个带有非线性结构、类别不平衡且包含冗余特征的三分类数据集。

我们将使用 sklearn 库来生成数据、构建模型并进行全面的评估和可视化。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.decomposition import PCA
from sklearn.metrics import (
    accuracy_score, f1_score, roc_auc_score, average_precision_score,
    roc_curve, precision_recall_curve, classification_report, confusion_matrix
)
from sklearn.preprocessing import label_binarize
from sklearn.inspection import permutation_importance
import warnings

RANDOM_STATE = 42
np.random.seed(RANDOM_STATE)

# 1) 构造数据集（多分类，非线性+冗余+噪声+不平衡）
n_samples = 3800
n_features_base = 8
X, y = make_classification(
    n_samples=n_samples, n_features=n_features_base,
    n_informative=4, n_redundant=2, n_repeated=0,
    n_classes=3, n_clusters_per_class=2,
    class_sep=1.2, flip_y=0.03,
    weights=[0.50, 0.35, 0.15],
    random_state=RANDOM_STATE
)

# 增加非线性派生特征（提升边界复杂度）
x_sin = np.sin(X[:, 0] * X[:, 1])
x_quad = X[:, 2]**2 - X[:, 3]
X = np.hstack([X, x_sin[:, None], x_quad[:, None]])  # 共10维

feature_names = [f"f{i}" for i in range(X.shape[1])]

# 划分训练集/测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.30, stratify=y, random_state=RANDOM_STATE
)

# 2) 训练主随机森林模型
rf = RandomForestClassifier(
    n_estimators=300,
    max_depth=None,
    max_features='sqrt',
    min_samples_split=2,
    min_samples_leaf=1,
    bootstrap=True,
    oob_score=True,
    n_jobs=-1,
    class_weight='balanced_subsample',
    random_state=RANDOM_STATE
)
with warnings.catch_warnings():
    warnings.simplefilter("ignore")  # 忽略部分版本下oob的提示
    rf.fit(X_train, y_train)

y_pred_test = rf.predict(X_test)
y_proba_test = rf.predict_proba(X_test)

# 计算评估指标
acc_test = accuracy_score(y_test, y_pred_test)
f1m_test = f1_score(y_test, y_pred_test, average='macro')
# 需要one-hot以支持多分类ROC/PR
classes = np.unique(y)
y_test_onehot = label_binarize(y_test, classes=classes)
# macro AUC
auc_macro = roc_auc_score(y_test_onehot, y_proba_test, average='macro', multi_class='ovr')
ap_macro = average_precision_score(y_test_onehot, y_proba_test, average='macro')

print("=== 主模型（全特征）评估 ===")
print(f"Test Accuracy: {acc_test:.4f}")
print(f"Test F1-macro: {f1m_test:.4f}")
print(f"Test ROC-AUC (macro-ovr): {auc_macro:.4f}")
print(f"Test Average Precision (macro): {ap_macro:.4f}")
print(f"OOB Score (RF内估计): {rf.oob_score_:.4f}")
print("\nClassification Report (Test):\n", classification_report(y_test, y_pred_test))
print("Confusion Matrix (Test):\n", confusion_matrix(y_test, y_pred_test))

# 3) 计算Permutation Importance（基于F1-macro）
perm = permutation_importance(
    rf, X_test, y_test, n_repeats=10, random_state=RANDOM_STATE, scoring='f1_macro', n_jobs=-1
)
mdi_importance = rf.feature_importances_
perm_importance = perm.importances_mean
# 排序（以MDI为主）
order = np.argsort(mdi_importance)[::-1]
topk = min(10, X.shape[1])
order_topk = order[:topk]
mdi_top = mdi_importance[order_topk]
perm_top = perm_importance[order_topk]
feat_top = [feature_names[i] for i in order_topk]

# 4) 为二维可视化，构造PCA投影并训练单独的2D-RF用于绘制决策边界
pca = PCA(n_components=2, random_state=RANDOM_STATE)
X_train_2d = pca.fit_transform(X_train)
X_test_2d = pca.transform(X_test)

rf2d = RandomForestClassifier(
    n_estimators=200,
    max_depth=None,
    max_features='sqrt',
    bootstrap=True,
    random_state=RANDOM_STATE
).fit(X_train_2d, y_train)

# 生成网格用于绘制决策边界
x_min, x_max = X_train_2d[:, 0].min() - 1.0, X_train_2d[:, 0].max() + 1.0
y_min, y_max = X_train_2d[:, 1].min() - 1.0, X_train_2d[:, 1].max() + 1.0
xx, yy = np.meshgrid(
    np.linspace(x_min, x_max, 400),
    np.linspace(y_min, y_max, 400)
)
grid_2d = np.c_[xx.ravel(), yy.ravel()]
proba_grid = rf2d.predict_proba(grid_2d)
label_grid = np.argmax(proba_grid, axis=1).reshape(xx.shape)
uncert_grid = 1.0 - np.max(proba_grid, axis=1).reshape(xx.shape)  # 不确定性：1-最大类概率

# 5) 计算ROC与PR曲线（micro）
y_score = y_proba_test
fpr_micro, tpr_micro, _ = roc_curve(y_test_onehot.ravel(), y_score.ravel())
prec_micro, rec_micro, _ = precision_recall_curve(y_test_onehot.ravel(), y_score.ravel())
auc_micro = roc_auc_score(y_test_onehot, y_score, average='micro', multi_class='ovr')
ap_micro = average_precision_score(y_test_onehot, y_score, average='micro')

# 6) 观察OOB与测试集准确率随树数变化的收敛趋势
n_list = [10, 30, 60, 120, 200, 400, 800]
oob_scores = []
test_accs = []
for n_est in n_list:
    rft = RandomForestClassifier(
        n_estimators=n_est,
        max_depth=None,
        max_features='sqrt',
        bootstrap=True,
        oob_score=True,
        n_jobs=-1,
        random_state=RANDOM_STATE,
        class_weight='balanced_subsample'
    )
    with warnings.catch_warnings():
        warnings.simplefilter("ignore")
        rft.fit(X_train, y_train)
    oob_scores.append(rft.oob_score_)
    y_pred_tt = rft.predict(X_test)
    test_accs.append(accuracy_score(y_test, y_pred_tt))

# 7) 绘制综合可视化分析图
plt.rcParams["figure.facecolor"] = "white"
plt.rcParams["axes.facecolor"] = "white"

fig = plt.figure(figsize=(16, 13))
gs = fig.add_gridspec(2, 2, wspace=0.25, hspace=0.25)

# 子图1：PCA-2D 决策边界 + 训练/测试点 + 不确定性等高线
ax1 = fig.add_subplot(gs[0, 0])
n_classes = len(classes)
cmap_label = sns.color_palette("bright", n_classes)
from matplotlib.colors import ListedColormap
cmap_bg = ListedColormap(sns.color_palette("bright", n_classes).as_hex())

ax1.contourf(xx, yy, label_grid, alpha=0.25, cmap=cmap_bg, levels=np.arange(n_classes+1)-0.5)
# 不确定性等高线
cs = ax1.contour(xx, yy, uncert_grid, levels=6, cmap="Greys", alpha=0.9, linewidths=1)
ax1.clabel(cs, inline=True, fontsize=8, fmt=lambda v: f"u={v:.2f}")

# 绘制训练/测试点
for k, col in zip(classes, cmap_label):
    ax1.scatter(X_train_2d[y_train==k, 0], X_train_2d[y_train==k, 1],
                c=[col], s=16, marker='o', edgecolor='k', linewidth=0.3, alpha=0.9, label=f"Train c{k}")
    ax1.scatter(X_test_2d[y_test==k, 0], X_test_2d[y_test==k, 1],
                c=[col], s=60, marker='^', edgecolor='k', linewidth=0.5, alpha=0.9, label=f"Test c{k}")
ax1.set_title("PCA-2D 决策边界与不确定性分布")
ax1.set_xlabel("PC1")
ax1.set_ylabel("PC2")
ax1.legend(ncol=3, fontsize=8, frameon=True)

# 子图2：ROC与PR曲线（micro曲线为主，宏平均AUC/AP给出数值）
ax2 = fig.add_subplot(gs[0, 1])
ax2.plot(fpr_micro, tpr_micro, color="#d62728", lw=2.0, label=f"ROC micro (AUC={auc_micro:.3f})")
# 为区分，PR放在同一坐标轴上但用虚线（注意刻度不同，仅作趋势参考）
ax2.plot(rec_micro, prec_micro, color="#1f77b4", lw=2.0, linestyle="--",
         label=f"PR micro (AP={ap_micro:.3f})")
# 加入基准线
ax2.plot([0, 1], [0, 1], color="gray", lw=1, alpha=0.5, label="ROC随机基线")
ax2.hlines(y=y_test_onehot.mean(), xmin=0, xmax=1, colors="gray", linestyles=":", lw=1,
           label="PR随机基线（正类比例）")
ax2.set_xlim(0, 1)
ax2.set_ylim(0, 1)
ax2.set_title("ROC与PR曲线对比（micro）")
ax2.set_xlabel("FPR / Recall")
ax2.set_ylabel("TPR / Precision")
ax2.legend(loc="lower right", frameon=True)

# 子图3：特征重要性对比（MDI vs Permutation）
ax3 = fig.add_subplot(gs[1, 0])
y_pos = np.arange(topk)
bar_w = 0.35
# 侧向条形图以便展示长名字
ax3.barh(y_pos - bar_w/2, mdi_top, height=bar_w, color="#ff7f0e", edgecolor="k", label="MDI")
ax3.barh(y_pos + bar_w/2, perm_top, height=bar_w, color="#2ca02c", edgecolor="k", label="Permutation (F1-macro)")
ax3.set_yticks(y_pos, labels=feat_top)
ax3.invert_yaxis()
ax3.set_title("特征重要性对比（MDI vs 置换）")
ax3.set_xlabel("重要性分数")
ax3.legend(frameon=True)

# 子图4：OOB分数与测试准确率随树数变化（收敛趋势）
ax4 = fig.add_subplot(gs[1, 1])
ax4.plot(n_list, oob_scores, marker="o", color="#e377c2", lw=2.0, label="OOB Score")
ax4.plot(n_list, test_accs, marker="s", color="#17becf", lw=2.0, label="Test Accuracy")
ax4.set_xscale("log")
ax4.set_xticks(n_list)
ax4.get_xaxis().set_major_formatter(plt.ScalarFormatter())
ax4.set_ylim(0, 1)
ax4.set_title("OOB与Test准确率随树数变化趋势")
ax4.set_xlabel("n_estimators（树数规模）")
ax4.set_ylabel("分数")
ax4.legend(frameon=True)

plt.tight_layout()
plt.show()

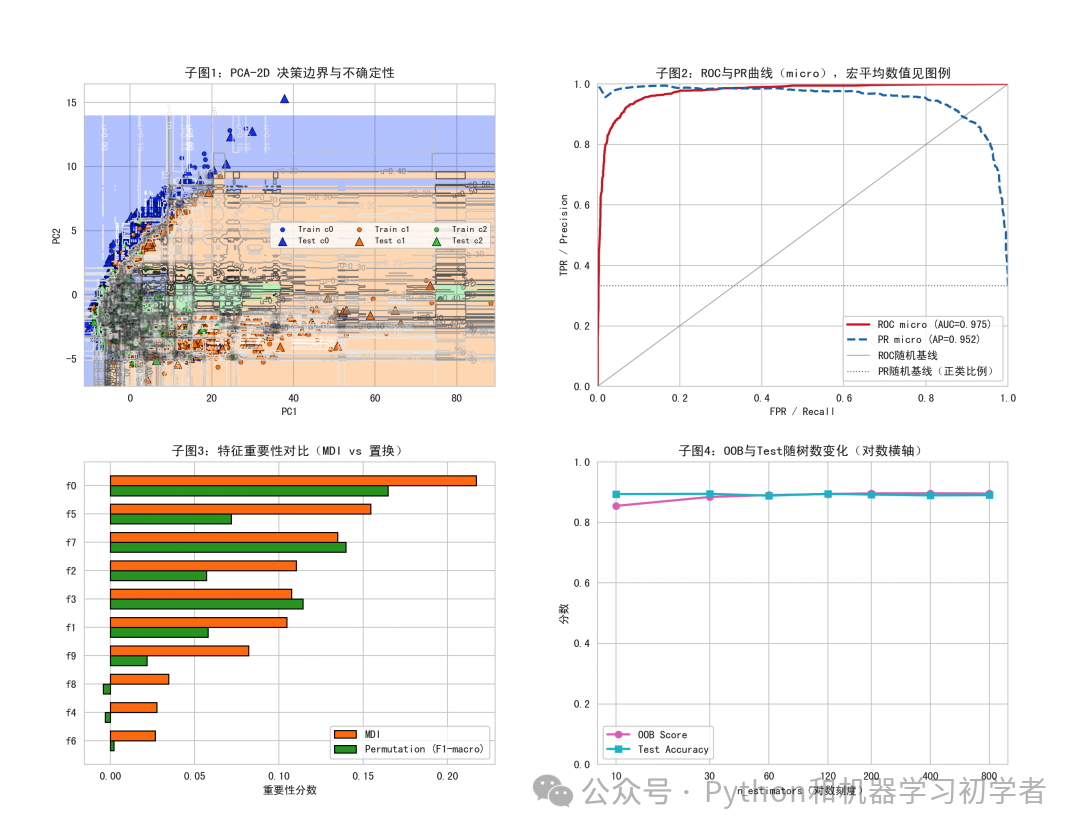
图1：PCA-2D决策边界与不确定性分布
为了直观展示随机森林学习到的复杂边界，我们将高维数据通过PCA降维至二维平面，并在此平面上重新训练一个随机森林（仅用于可视化）。背景色块代表模型的预测类别，而灰色的等高线则表示模型预测的不确定性（1 - 最大类概率）。可以看到，随机森林能够拟合出非线性的决策边界，并且在类别边界附近，模型的不确定性也相应更高。

图2：ROC与PR曲线对比
对于多分类问题，我们采用One-vs-Rest策略计算了micro平均的ROC曲线和PR曲线。图中红色实线为ROC曲线，蓝色虚线为PR曲线。ROC曲线下的面积和PR曲线下的平均精度都接近于1，表明模型在三分类不平衡任务上依然保持了优异的整体区分能力。

图3：特征重要性对比（MDI vs 置换）
该条形图对比了两种特征重要性评估方法的结果。MDI（基于不纯度下降）和置换重要性（基于F1-macro分数下降）的排序总体一致，但在具体数值上有所差异。例如，特征f0在两种方法中都最为重要，而一些非线性派生特征的重要性则有所不同。这种对比为我们理解特征贡献提供了更全面的视角，也是进行特征选择 的重要参考。

图4：OOB与Test准确率随树数变化趋势
该图展示了模型性能如何随着森林中决策树数量的增加而变化。可以看到，无论是内部的OOB估计分数还是外部的测试集准确率，都随着树的数量增加而快速提升并逐渐收敛。这证实了增加树的数量可以有效提升模型的稳定性和性能，但超过一定数量后，收益会递减。

总结

原理层面，随机森林通过 Bagging 和 特征随机子空间 的双重随机性，巧妙地降低了高方差基学习器（决策树）集成的方差，其理论边界由单棵树的“强度”和树间的“相关性”共同决定。

实践层面，它具有多重优势：

1. 出色的泛化能力：能有效处理非线性关系和高维数据，对过拟合有较强的抵抗力。
2. 内置评估工具：OOB估计提供了便捷且可靠的泛化误差评估，无需额外验证集。
3. 提供模型解释：通过MDI和置换重要性，我们可以洞察哪些特征对预测起关键作用。
4. 工程友好：训练过程高度可并行，预测速度快。

在本文的案例中，随机森林成功应对了一个构造的、包含非线性、类别不平衡和冗余噪声的三分类难题，各项评估指标均表现优异。可视化分析进一步揭示了其决策边界、不确定性分布、特征重要性以及随着模型规模扩大的收敛趋势。

总而言之，随机森林因其强大的性能、良好的鲁棒性、天然的可并行性以及一定的可解释性，至今仍然是解决分类和回归问题的首选实用算法之一，非常值得深入学习和掌握。如果你想了解更多关于集成学习 或其他机器学习算法的深度讨论，欢迎到云栈社区的技术板块交流探讨。