LeetCode算法题解：合并K个排序链表的三种高效实现（分治法/优先队列）

本文将详细讲解如何高效地合并 K 个已排序的链表。这是 LeetCode 上的一道经典题目，是基础两链表合并问题的进阶版。我们将探讨三种主流解法：直观的暴力法、高效的分治与迭代法，以及利用数据结构的优先队列法，并重点分析后两者的实现细节与代码。

题目描述

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例：

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

解题思路分析

解决此问题，主要有三个方向：

1. 暴力法：遍历所有链表节点，将值存入数组，对数组排序后，再重新构建链表。此方法思路简单，但时间复杂度和空间复杂度都较高，非最优解。
2. 分治法（推荐）：核心是归并分治思想。将 K 个链表的合并问题，递归地分解为两两合并的子问题，直至子问题可直接求解（单个链表），再逐层合并结果。这与归并排序的流程高度一致。此方法时间复杂度为 O(N log K)，空间复杂度为 O(1)（递归栈开销不计入额外空间）。
   • 迭代版本：一种更直观、易于理解的分治实现。它自底向上，逐轮两两合并链表，直到最终只剩下一个链表。
3. 优先队列/最小堆法：利用priority_queue（默认最小堆）动态维护当前 K 个链表头节点中的最小值。每次弹出最小值节点，并将其下一个节点加入队列，直到队列为空。此方法同样高效，是学习数据结构中堆应用的绝佳案例。

下面重点介绍分治法和优先队列法的具体实现。

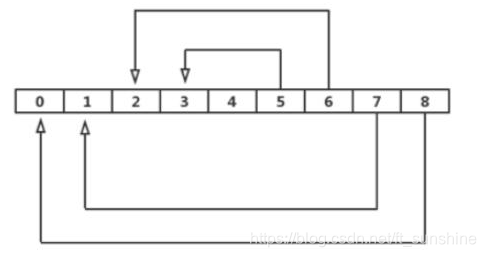
迭代法合并过程示意图（一轮）：将第 i 个与第 len-1-i 个链表合并。

迭代法（分治）流程简述：

1. 初始时，链表数组长度为 len。
2. 当 len > 1 时循环：
   • 将第 i 个链表与第 len-1-i 个链表两两合并（i 从 0 到 len/2），结果存回数组前部。
   • 更新 len = (len + 1) / 2，即新一轮待合并的链表数量。
3. 循环结束，数组第一个元素即为最终合并后的链表头节点。

参考代码实现

1. 分治法：递归版（二分+递归）

此版本清晰地体现了分治的递归思想。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int length = lists.size();
        if(length == 0) return nullptr;
        if(length == 1) return lists[0];

        // 进入二分递归合并流程
        return binaryMerge(lists, 0, length-1);
    }

    // 二分递归合并函数
    ListNode* binaryMerge(vector<ListNode*> &lists, int left, int right){
        // 递归出口：当区间内只有一个链表时
        if(left == right) return lists[left];

        int mid = (left + right) >> 1; // 取中点
        // 递归合并左半部分和右半部分
        ListNode* listOfLeft = binaryMerge(lists, left, mid);
        ListNode* listOfRight = binaryMerge(lists, mid+1, right);

        // 合并两个已排序链表（可递归可迭代）
        return mergeRecursively(listOfLeft, listOfRight);
    }

    // 递归合并两个链表的函数
    ListNode* mergeRecursively(ListNode* pHead1, ListNode* pHead2){
        if(pHead1 == nullptr) return pHead2;
        if(pHead2 == nullptr) return pHead1;

        if(pHead1->val <= pHead2->val){
            pHead1->next = mergeRecursively(pHead1->next, pHead2);
            return pHead1;
        }else{
            pHead2->next = mergeRecursively(pHead1, pHead2->next);
            return pHead2;
        }
    }

    // （备选）迭代合并两个链表的函数，更推荐使用
    ListNode* mergeIteratively2(ListNode* pHead1, ListNode* pHead2){
        ListNode* pNode = new ListNode(-1); // 哑节点
        ListNode* pDummyHead = pNode;
        while(pHead1 != nullptr && pHead2 != nullptr){
            if(pHead1->val < pHead2->val){
                pNode->next = pHead1;
                pHead1 = pHead1->next;
            }else{
                pNode->next = pHead2;
                pHead2 = pHead2->next;
            }
            pNode = pNode->next;
        }
        // 链接剩余部分
        pNode->next = pHead1 == nullptr? pHead2: pHead1;
        return pDummyHead->next;
    }
};

2. 分治法：迭代版（更简单，推荐）

此版本代码更简洁，无需递归，直接模拟归并排序的合并阶段。

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int len = lists.size();
        if(len == 0) return nullptr;
        if(len == 1) return lists[0];

        // 循环两两合并，直到只剩下一个链表
        while(len > 1){
            for(int i = 0; i < len/2; i++)
                // 合并第 i 个和第 len-1-i 个链表
                lists[i] = mergeIteratively(lists[i], lists[len-1-i]);
            len = (len + 1) / 2; // 更新待合并链表数量
        }
        return lists[0];
    }

    // 迭代合并两个链表
    ListNode* mergeIteratively(ListNode* pHead1, ListNode* pHead2){
        ListNode dummyHead(-1);
        ListNode* pNode = &dummyHead;
        while(pHead1 && pHead2){
            if(pHead1->val < pHead2->val){
                pNode->next = pHead1;
                pHead1 = pHead1->next;
            }else{
                pNode->next = pHead2;
                pHead2 = pHead2->next;
            }
            pNode = pNode->next;
        }
        pNode->next = pHead1 ? pHead1 : pHead2;
        return dummyHead.next;
    }
};

3. 优先队列/最小堆法

此方法利用了priority_queue这一数据结构，其核心在于自定义比较规则以构建最小堆。

// 方法一：通过结构体自定义比较函数
class Solution {
public:
    struct cmp{
        bool operator()(const ListNode* a , const ListNode* b){  
            return a->val > b->val; // 注意是 >，构建最小堆
        }
    };

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.empty()) return nullptr;

        priority_queue<ListNode*, vector<ListNode*>, cmp> minHeap;
        // 将所有链表的头节点加入最小堆
        for (auto& p: lists) {
            if (p) minHeap.push(p);
        }

        ListNode dummyHead(-1);
        auto pNode = &dummyHead;
        while (!minHeap.empty()) {
            auto cur = minHeap.top(); minHeap.pop(); // 取出当前最小值节点
            if (cur->next) minHeap.push(cur->next); // 将该节点的下一个加入堆
            pNode->next = cur;
            pNode = cur; // pNode = pNode->next;
        }
        return dummyHead.next;
    }
};

// 方法二：使用 lambda 表达式和 function 类型自定义比较（C++11及以上）
class Solution {
public:
    typedef function<bool(const ListNode*, const ListNode*)> Compare;

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.empty()) return nullptr;
        // 定义比较规则：值小的优先级高（最小堆）
        Compare cmp = [](const ListNode *a, const ListNode *b) {
            return a->val > b->val;
        };
        priority_queue<ListNode*, vector<ListNode*>, Compare> minHeap(cmp);

        for (auto& p: lists) {
            if (p) minHeap.push(p);
        }

        ListNode dummyHead(-1);
        auto pNode = &dummyHead;
        while (!minHeap.empty()) {
            auto cur = minHeap.top(); minHeap.pop();
            if (cur->next) minHeap.push(cur->next);
            pNode->next = cur;
            pNode = cur;
        }
        return dummyHead.next;
    }
};

总结

解决“合并K个排序链表”问题，分治迭代法和优先队列法都是时间复杂度为 O(N log K) 的优秀算法。分治法的思想与归并排序同源，有助于加深对分治策略的理解；而优先队列法则是对标准库数据结构的巧妙应用。在面试或实际编码中，可根据对代码简洁性或特定数据结构的要求进行选择。理解这两种方法的本质，对于提升解决复杂链表问题和数据结构应用能力大有裨益。