向量运算核心原理：从几何基础到机器学习与物理应用

向量是一个有方向的量，兼具大小（模长）与方向。这种特性使其成为描述物理世界中众多现象的理想工具，例如速度、风力或作用力。

坐标表示

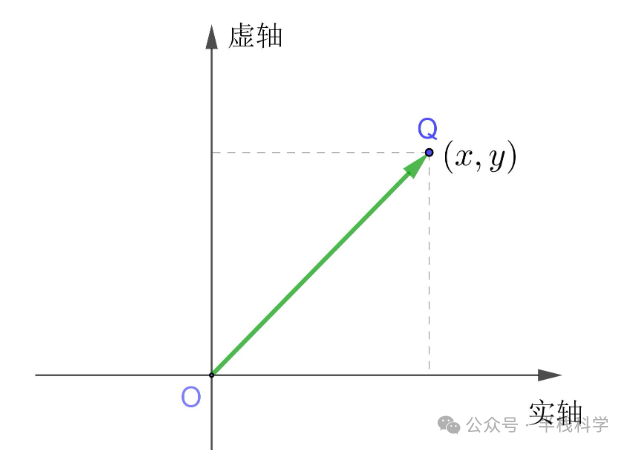
在数学中，向量常用坐标表示；在几何中，则用箭头直观展示，箭头长度代表大小，指向代表方向。

• 二维向量: →v = (x, y)，模长为 |→v| = √(x² + y²)。
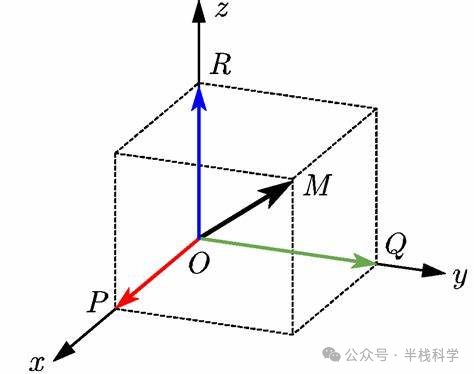
• 三维向量: →v = (x, y, z)，模长为 |→v| = √(x² + y² + z²)。
• N维向量: →v = (x₁, x₂, ..., xn)，模长为 |→v| = √(x₁² + x₂² + ... + xn²)。

二、向量的加减法

向量加法

给定向量 →a = (x₁, y₁), →b = (x₂, y₂)，其和为：
→a + →b = (x₁ + x₂, y₁ + y₂)

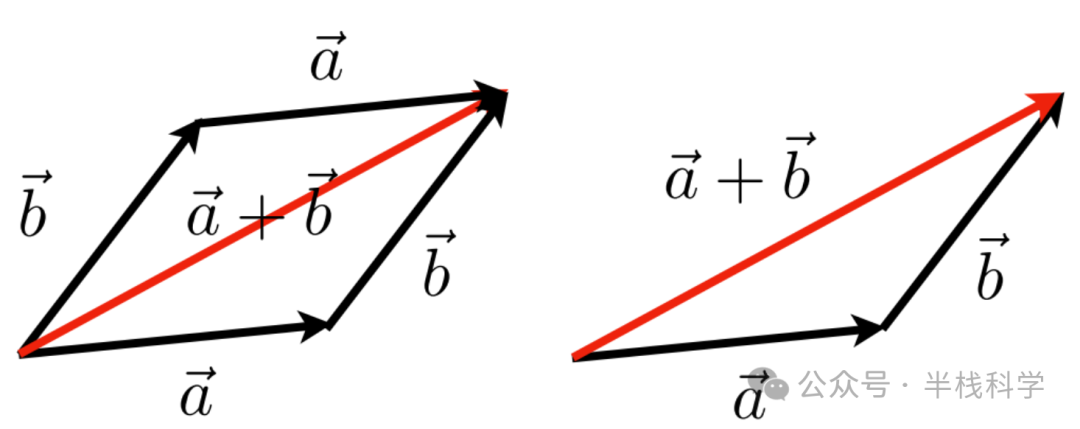
几何上，加法遵循三角形或平行四边形法则，可理解为先沿 →a 移动，再沿 →b 移动。

应用示例：力的合成
两股力 →F₁ = (3, 4), →F₂ = (1, 2)，其合力为：
→F = →F₁ + →F₂ = (4, 6)

向量减法

给定向量 →a = (x₁, y₁), →b = (x₂, y₂)，其差为：
→a - →b = (x₁ - x₂, y₁ - y₂)

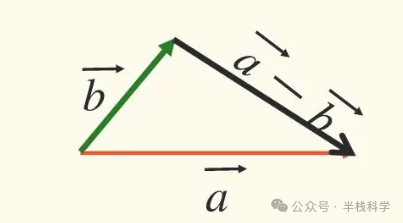
几何上，→a - →b 是从 →b 终点指向 →a 终点的向量。

应用示例：相对速度计算
船速 →v_船 = (8, 0)（东），水流速 →v_水 = (3, 1)（东偏北），则船相对于水的速度为：
→v_相对 = (8-3, 0-1) = (5, -1)（东偏南）

三、向量内积（点积）

向量的内积（Dot Product）是两个向量对应分量乘积之和，结果是一个标量。
给定 →a = (x₁, y₁), →b = (x₂, y₂)：
→a · →b = x₁x₂ + y₁y₂

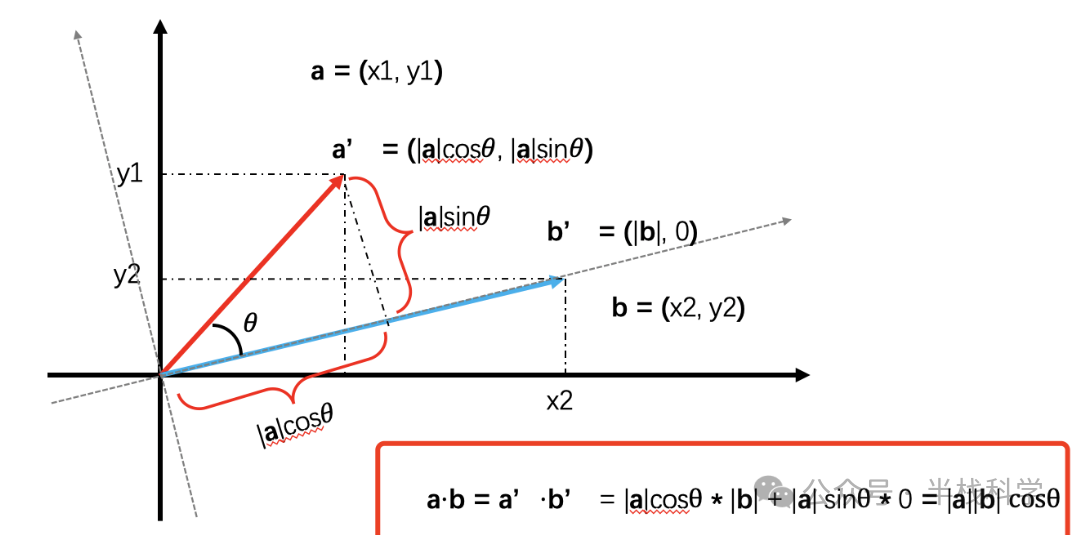
其几何意义为：
→a · →b = |→a| |→b| cosθ
其中 θ 为两向量夹角。由此可知：

• 夹角越小，内积越大。
• 向量垂直时，内积为0。
• 内积在坐标旋转下保持不变。

应用示例：商品推荐与余弦相似度
电商平台的“相似产品”推荐常基于余弦相似度实现，其核心是仅比较向量方向，忽略模长影响。实现步骤如下：

1. 特征向量化：将商品信息（类目、品牌、价格、文本描述、图片特征等）转化为特征向量 →g。
2. L2归一化：对向量进行归一化处理，使模长为1。对于分量 x_k，归一化值为 X_k = x_k / √(Σx_i²)。得到单位向量 →G。
3. 计算相似度：两个商品的相似度简化为其归一化向量的点积：similarity = →G₁ · →G₂。
   向量点积是评估特征方向相似性的重要工具，在推荐系统和机器学习中广泛应用。

四、向量外积（叉积）

向量的外积（Cross Product，仅适用于三维空间）的结果是一个垂直于原向量所在平面的新向量。
给定三维向量 →a, →b，其外积 →c = →a × →b：

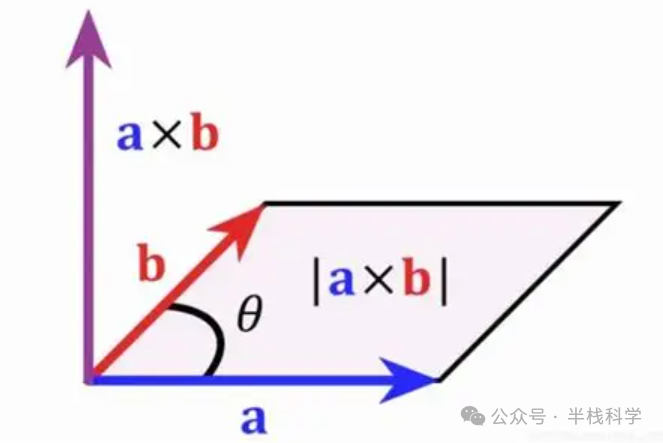
• 模长：|→c| = |→a| |→b| sinθ，几何上等于以两向量为边的平行四边形面积。
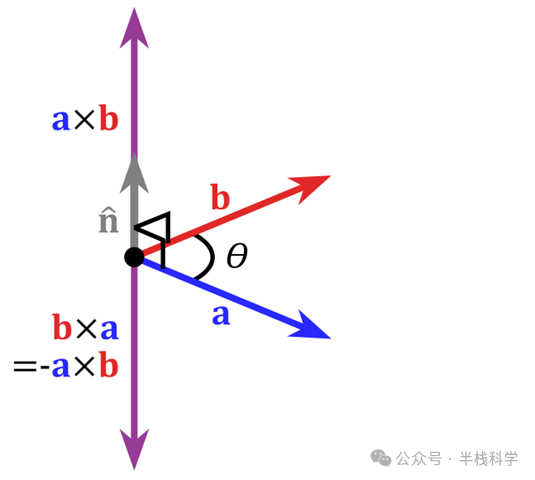
• 方向：垂直于 →a 与 →b 构成的平面，遵循右手螺旋定则（四指从 →a 转向 →b，拇指方向为 →c 方向）。因此 →a × →b = - (→b × →a)。

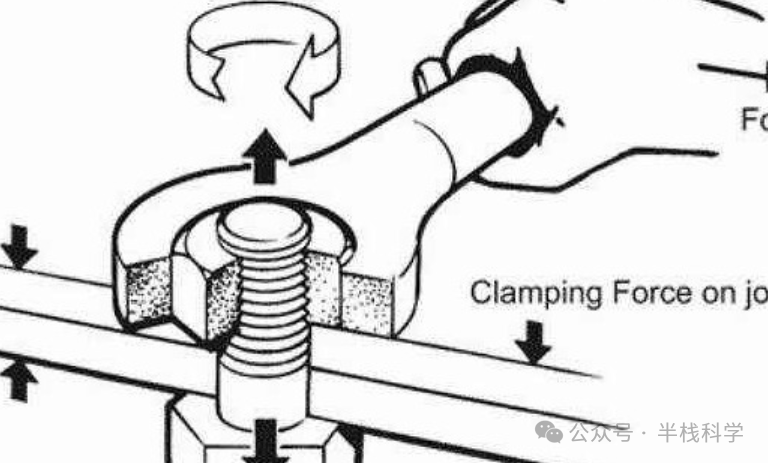
应用示例：力矩计算
力矩描述力使物体绕轴旋转的能力，公式为：
→τ = →r × →F
其中 →r 为从旋转中心到施力点的位矢，→F 为作用力。力矩大小等于 |→r| |→F| sinθ，方向由右手定则确定。

五、动手实践：使用 Python 实现

以下使用 Python 的 NumPy 库演示上述运算。

import numpy as np

# 定义两个三维向量
a = np.array([3, 4, 0])
b = np.array([4, 0, 3])

# 1️⃣ 向量加法
add = a + b
print("加法 a + b =", add)

# 2️⃣ 向量减法
sub = a - b
print("减法 a - b =", sub)

# 3️⃣ 向量内积（点积）
dot = np.dot(a, b)
print("内积 a · b =", dot)

# 4️⃣ L2归一化
a_norm = a / np.linalg.norm(a)
b_norm = b / np.linalg.norm(b)
print("归一化后的 a =", a_norm)
print("归一化后的 b =", b_norm)

# 5️⃣ 余弦相似度 (归一化后点积)
cos_sim = np.dot(a_norm, b_norm)
print("余弦相似度 =", cos_sim)

# 6️⃣ 向量外积（叉积，仅三维）
cross = np.cross(a, b)
print("外积 a × b =", cross)

执行输出：

加法 a + b = [7 4 3]
减法 a - b = [-1  4 -3]
内积 a · b = 12
归一化后的 a = [0.6 0.8 0. ]
归一化后的 b = [0.8 0.  0.6]
余弦相似度 = 0.48
外积 a × b = [ 12  -9 -16]

六、总结

向量是连接数学、物理学与计算机科学的桥梁。从基础的加减法描述相对运动，到内积支撑的推荐算法与机器学习模型，再到外积在力学与图形学中的关键作用，深入理解向量运算的原理，是掌握现代人工智能与工程仿真技术的重要基石。