内存访问与CPU缓存：C语言中二维数组行遍历为何优于列遍历

在程序性能优化中，理解内存的访问模式至关重要。本文将通过两个C语言代码示例，深入探讨为何在二维数组操作中，行优先遍历（Row-major）的性能通常远高于列优先遍历（Column-major），并分享几种行之有效的优化技巧。

示例一：内存分配策略的性能差异

我们先从一个更基础的例子入手，直观感受单次操作与多次操作的性能差距：在循环内反复分配小块内存，还是一次性分配一大块内存更快？

// 在循环内分配
for(int i = 0; i < n; i++) {
    char *buf = malloc(1024);
    // 使用buf
    free(buf);
}

// 一次性分配
char *buf = malloc(1024 * n);
for(int i = 0; i < n; i++) {
    // 使用buf偏移量进行访问
}
free(buf);

结论
毫无疑问，一次性分配（第二种方法）的速度显著更快。

代码验证（加入calloc对比）

为了量化这种差异，我们编写了以下基准测试代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

#define N 10000
#define BUF_SIZE 1024

// 方法1：循环内分配
void method1() {
    clock_t start = clock();
    for (int i = 0; i < N; i++) {
        char *buf = malloc(BUF_SIZE);
        if (!buf) {
            printf("内存分配失败!\n");
            return;
        }
        free(buf);
    }
    clock_t end = clock();
    printf("循环内分配: %.6f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
}

// 方法2：一次性分配
void method2() {
    clock_t start = clock();
    // 一次性分配所有内存
    char *buf = malloc(BUF_SIZE * N);
    if (!buf) {
        printf("内存分配失败!\n");
        return;
    }
    free(buf);
    clock_t end = clock();
    printf("一次性分配: %.6f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
}

// 方法3：使用calloc
void method3() {
    clock_t start = clock();
    char *buf = calloc(N, BUF_SIZE);
    if (!buf) {
        printf("内存分配失败!\n");
        return;
    }
    free(buf);
    clock_t end = clock();
    printf("calloc分配: %.6f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
}

int main() {
    printf("测试 %d 次分配，每次 %d 字节\n\n", N, BUF_SIZE);
    method1();
    method2();
    method3();
    return 0;
}

验证结论

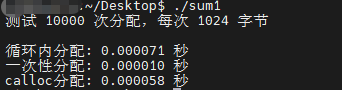
测试结果显示，循环分配与一次性分配的时间差达到了数倍，且这种差异会随着申请内存块的大小线性增长。

性能分析

• 循环分配：每次调用malloc都需要系统遍历内存空闲链表来寻找合适空间，开销巨大。多次分配得到的内存地址通常是分散、不连续的，导致内存碎片率高。后续访问这些碎片化内存会产生更多的随机内存访问，对CPU缓存极不友好。
• 一次性分配：单次系统调用完成大块连续内存的分配，极大减少了内存碎片。连续的内存布局使得程序的访问模式更具可预测性，能更好地利用CPU缓存，从而获得更快的访问速度。

示例二：二维数组求和，行遍历与列遍历的终极对决

现在我们将核心问题具体化：对于一个充满随机数（小于100）的大型二维数组，求所有元素之和，是行遍历求和快还是列遍历求和快？

初步结论：行求和明显更快。

为了验证这一点，我们设计了严谨的测试代码：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

#define ROWS 5000
#define COLS 5000

// 初始化数组
void init_array(int arr[ROWS][COLS]) {
    srand(42);
    for (int i = 0; i < ROWS; i++) {
        for (int j = 0; j < COLS; j++) {
            arr[i][j] = rand() % 100; // 生成0-99的随机数
        }
    }
}

// 行求和（基础版）
long long sum_by_rows(int arr[ROWS][COLS]) {
    long long total = 0;
    for (int i = 0; i < ROWS; i++) {
        for (int j = 0; j < COLS; j++) {
            total += arr[i][j];
        }
    }
    return total;
}

// 列求和（基础版）
long long sum_by_cols(int arr[ROWS][COLS]) {
    long long total = 0;
    for (int j = 0; j < COLS; j++) {
        for (int i = 0; i < ROWS; i++) {
            total += arr[i][j];
        }
    }
    return total;
}

// 验证所有方法结果是否一致
int verify_results(long long results[], int count, const char* names[]) {
    for (int i = 1; i < count; i++) {
        if (results[i] != results[0]) {
            printf("错误: %s 的结果不一致!\n", names[i]);
            printf("  %s: %lld\n", names[0], results[0]);
            printf("  %s: %lld\n", names[i], results[i]);
            return 0;
        }
    }
    return 1;
}

// 性能测试函数
void benchmark(const char* name, long long (*func)(int[ROWS][COLS]), int arr[ROWS][COLS], long long *result) {
    clock_t start, end;
    double cpu_time_used;
    start = clock();
    *result = func(arr);
    end = clock();
    cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;
    printf("%-10s 耗时: %.4f 秒, 结果: %lld\n", name, cpu_time_used, *result);
}

int main() {
    // 动态分配大数组，避免栈溢出
    printf("分配 %d x %d 数组 (约 %.2f MB)...\n", ROWS, COLS, (double)ROWS * COLS * sizeof(int) / (1024 * 1024));
    int (*arr)[COLS] = malloc(ROWS * sizeof(*arr));
    if (!arr) {
        printf("内存分配失败!\n");
        return 1;
    }

    printf("初始化数组...\n");
    init_array(arr);

    printf("\n开始性能测试:\n");
    printf("=============================================\n");

    // 存储各种方法的结果
    long long results[2];
    const char* method_names[2] = {
        "行求和(基础)",
        "列求和(基础)",
    };

    // 执行基准测试
    benchmark(method_names[0], sum_by_rows, arr, &results[0]);
    benchmark(method_names[1], sum_by_cols, arr, &results[1]);

    // 验证结果一致性
    printf("\n验证结果一致性...\n");
    if (verify_results(results, 2, method_names)) {
        printf("✓ 所有方法结果一致\n");
    }
    printf("=============================================\n");

    // 释放内存
    free(arr);
    printf("\n测试完成!\n");
    return 0;
}

测试结果

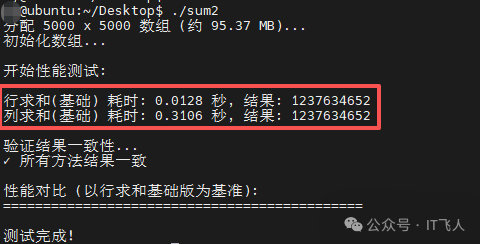
测试数据清晰地表明，行求和的速度远远超过列求和。

核心原理
这背后的核心原因，依然是内存的访问速度，更具体地说，是CPU缓存的利用效率。在C语言中，二维数组在内存中是按行连续存储的（行优先顺序）。行遍历时，访问的是连续的内存地址，CPU可以高效地将一整块数据预取到高速缓存中。而列遍历需要跨行访问，每次访问的地址都相隔甚远，导致缓存命中率极低，大量时间耗费在从主存读取数据上。

进阶优化：让行遍历更快

既然行遍历已经占优，我们能否让它更进一步？以下是三种常见的优化手段：

1. 优化版本1：在行循环内使用局部变量累加，减少对全局累加器的访问。
2. 优化版本2：应用循环展开（Loop Unrolling）技术，减少循环控制开销。
3. 优化版本3：采用分块（Blocking）策略，使工作集更适配CPU缓存大小。

综合验证代码

// ... 初始化、基础行求和、基础列求和函数与上文相同，此处省略 ...

// 优化版本1：行求和，使用局部变量减少内存访问
long long sum_by_rows_optimized(int arr[ROWS][COLS]) {
    long long total = 0;
    for (int i = 0; i < ROWS; i++) {
        long long row_sum = 0; // 使用局部变量
        for (int j = 0; j < COLS; j++) {
            row_sum += arr[i][j];
        }
        total += row_sum;
    }
    return total;
}

// 优化版本2：行求和，循环展开
long long sum_by_rows_unrolled(int arr[ROWS][COLS]) {
    long long total = 0;
    const int UNROLL = 4;
    for (int i = 0; i < ROWS; i++) {
        long long row_sum = 0;
        int j = 0;
        // 手动循环展开
        for (; j + UNROLL <= COLS; j += UNROLL) {
            row_sum += arr[i][j] + arr[i][j+1] + arr[i][j+2] + arr[i][j+3];
        }
        // 处理剩余元素
        for (; j < COLS; j++) {
            row_sum += arr[i][j];
        }
        total += row_sum;
    }
    return total;
}

// 优化版本3：分块求和（更好利用缓存）
long long sum_by_rows_blocked(int arr[ROWS][COLS]) {
    long long total = 0;
    const int BLOCK_SIZE = 256; // 选择适合缓存大小的块
    for (int bi = 0; bi < ROWS; bi += BLOCK_SIZE) {
        for (int i = bi; i < bi + BLOCK_SIZE && i < ROWS; i++) {
            long long row_sum = 0;
            for (int j = 0; j < COLS; j++) {
                row_sum += arr[i][j];
            }
            total += row_sum;
        }
    }
    return total;
}

// ... benchmark和main函数需要相应扩展以测试这3个新函数 ...

优化结果对比

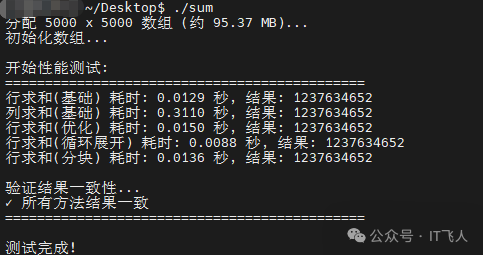
最终性能排序（由快到慢）：行求和(循环展开) > 行求和(基础) > 行求和(分块) > 行求和(局部变量优化) > 列求和(基础)。

总结与启示

1. 内存访问模式至上：在算法和数据结构的设计中，除了时间复杂度，必须考虑数据在内存中的布局和访问顺序。对于多维数组，坚持按存储顺序（在C/C++中是行优先）进行遍历是基本准则。
2. 理解CPU缓存：现代计算机系统的性能瓶颈常常在于内存访问。编写缓存友好的代码，往往比单纯减少算法步骤带来的收益更大。
3. 优化技巧的有效性：循环展开等优化技巧在特定场景下有效，但其效果受编译器优化等级、硬件架构等因素影响，最终应以实际性能测试为准。
4. 思维迁移：这一原理不仅适用于C语言，对于任何按行优先存储数据的语言或环境（如NumPy默认的C顺序）都同样重要。理解这些底层原理，是进行高性能编程和系统调优的关键，也是深入理解计算机系统和网络底层知识的重要一环。