夏普比率深度解析：量化投资中风险调整后收益的核心指标与应用

在量化投资领域，夏普比率（Sharpe Ratio）是评估投资策略绩效的基石。它不仅是衡量单一资产优劣的工具，其思想更贯穿于投资组合的构建、风险分散、相关性分析乃至杠杆运用等核心环节。对于希望建立系统化投资思维的人而言，深入理解夏普比率是至关重要的一步。

尽管其数学形式简洁，但夏普比率蕴含了深刻的金融逻辑：它将收益与风险统一考量，量化了“每承担一单位风险所能获得的超额回报”。这让我们得以穿透单纯收益率的表象，做出更为理性和稳健的决策。

一、为什么不能只看收益率？

仅凭总回报率做投资决策，往往会导致严重的判断偏差。我们可以通过一个简单案例来理解：

假设有两个投资标的，在一段时间后都实现了40%的总回报。

• 绿色标的：其价格走势平稳上升，波动极小。
• 黑色标的：虽然最终回报相同，但过程经历剧烈震荡，中途出现过大幅回撤。

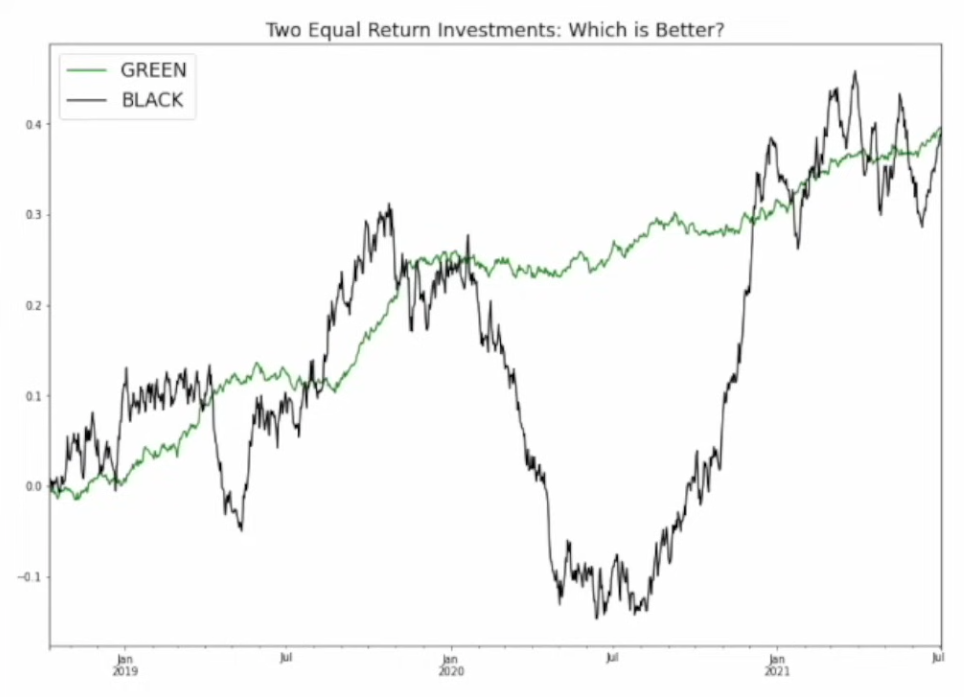
尽管结局相同，但直觉上我们会认为绿色标的更优，原因在于其承担的风险更低。这里的“风险”具体体现为：

1. 巨大的心理压力：黑色标的的深度回撤会显著增加持有者的焦虑。行为金融学指出，损失带来的痛苦感远超同等收益的愉悦感。
2. 对未来的信心不足：剧烈的波动会削弱投资者对其未来持续性的判断。相比之下，平稳增长的绿色标的更具可预测性。
3. 潜在的流动性风险：若在市场低点急需用钱，持有黑色标的可能被迫以亏损价格卖出，造成实际损失。

核心结论：在收益率相同的情况下，波动越大，真实的投资体验和潜在回报质量越差。因此，引入风险调整机制势在必行。

二、如何量化风险？理解波动率

为了科学评估风险，我们需要一个可测量的代理变量。最常用的就是波动率（Volatility），它被定义为收益率序列的标准差，通常用符号σ表示。

波动率的计算公式为：

[
\sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (r_i - \bar{r})^2}
]

其中：

• ( r_i )：第i期的收益率
• ( \bar{r} )：所有观测期的平均收益率
• ( N )：观测期总数

我们可以将其可视化理解：

• 图中的橙色线代表平均回报趋势（期望收益）。
• 蓝色曲线是实际的价格回报路径。
• 红色箭头则标示了每一期实际回报与平均回报之间的偏差。

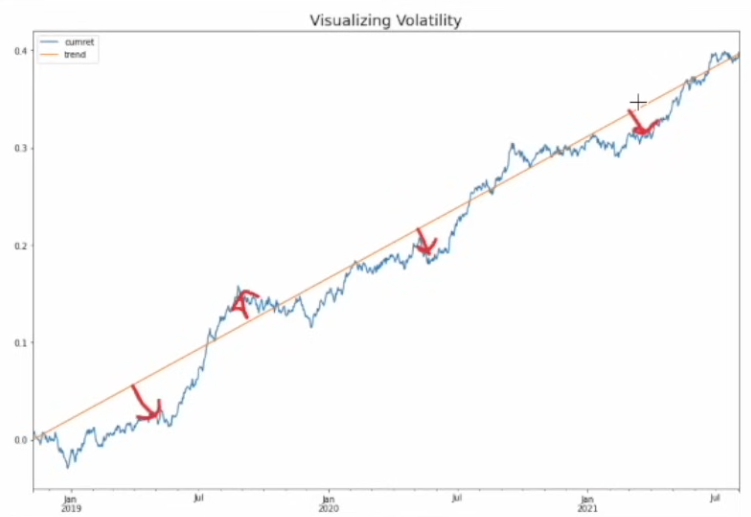
波动率正是对这些“偏差”或“波动幅度”的量化。波动越大，代表资产价格的不确定性越高，投资者承受的心理压力和潜在损失风险也越大。

三、夏普比率的定义与计算逻辑

基本公式

夏普比率最常用的简化公式为：
[
\text{夏普比率} = \frac{\text{平均收益率}}{\text{波动率}}
]

注：严格的定义应使用“超额收益率”（即资产收益率减去无风险利率），但在低利率环境下，常简化为上述形式。

核心逻辑

• 分子（收益）越高 → 比率值越高。
• 分母（风险/波动）越大 → 比率值越低。

这完美契合了投资者的根本追求：高收益、低风险。夏普比率越高，意味着承担每一单位风险所获得的补偿（收益）就越丰厚。

年度化处理

由于分析时使用的数据频率不同（如日度、月度），我们需要进行标准化调整以确保可比性：

• 基于日度数据计算时，通常乘以 (\sqrt{252})（约15.87），因为一年约有252个交易日。
• 基于月度数据计算时，则乘以 (\sqrt{12})（约3.46）。

四、实战应用：夏普比率如何揭示绩效差异？

让我们回到最初的案例。通过计算可得：

• 绿色标的的夏普比率：约为 2.0
• 黑色标的的夏普比率：约为 0.5

尽管总回报相同，但夏普比率清晰无误地显示：绿色标的的风险调整后表现远超黑色标的。这个数值结果与我们的直观感受完全一致，验证了该指标的有效性。

进一步，我们可以观察不同夏普比率所对应的理论回报路径：

• 夏普比率 = 2：路径较为稳定，波动较小。
• 夏普比率 = 5：波动极低，接近理想状态。
• 夏普比率 = 20：路径几乎呈直线，代表近乎无风险的套利机会（现实中极难持续存在）。

五、现实参照：怎样的夏普比率算优秀？

投资主体	长期夏普比率（参考）
标普500指数（SPY ETF）	≈ 0.45
沃伦·巴菲特的投资业绩	≈ 0.75
优秀的对冲基金	通常 > 2.0

一个现实可行的目标是：长期持续实现夏普比率在2.0以上，这足以让你超越市场上绝大多数投资者。

六、在投资组合构建中的核心作用

单一资产的局限性
假设有红色和蓝色两种资产：

• 两者的夏普比率均为 2.0。
• 预期收益和波动率也相同。

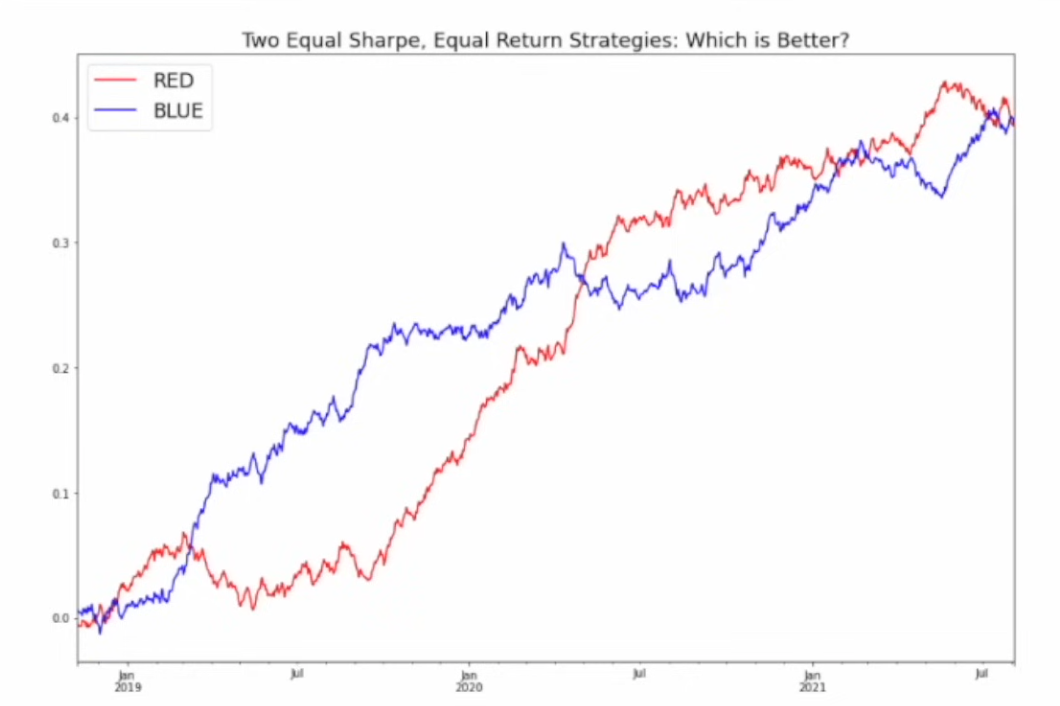
仅从单一指标看，二者无差异。但如果忽略它们之间的相关性，就会错失关键的优化机会。

关键洞察：负相关性的威力
假设红色与蓝色资产的价格运动方向经常相反（即呈现负相关性）：当红色上涨时，蓝色下跌，反之亦然。这种特性为风险对冲提供了天然基础。

组合优化效果
当我们构建一个50/50的等权重投资组合（图中紫色曲线），奇迹发生了：

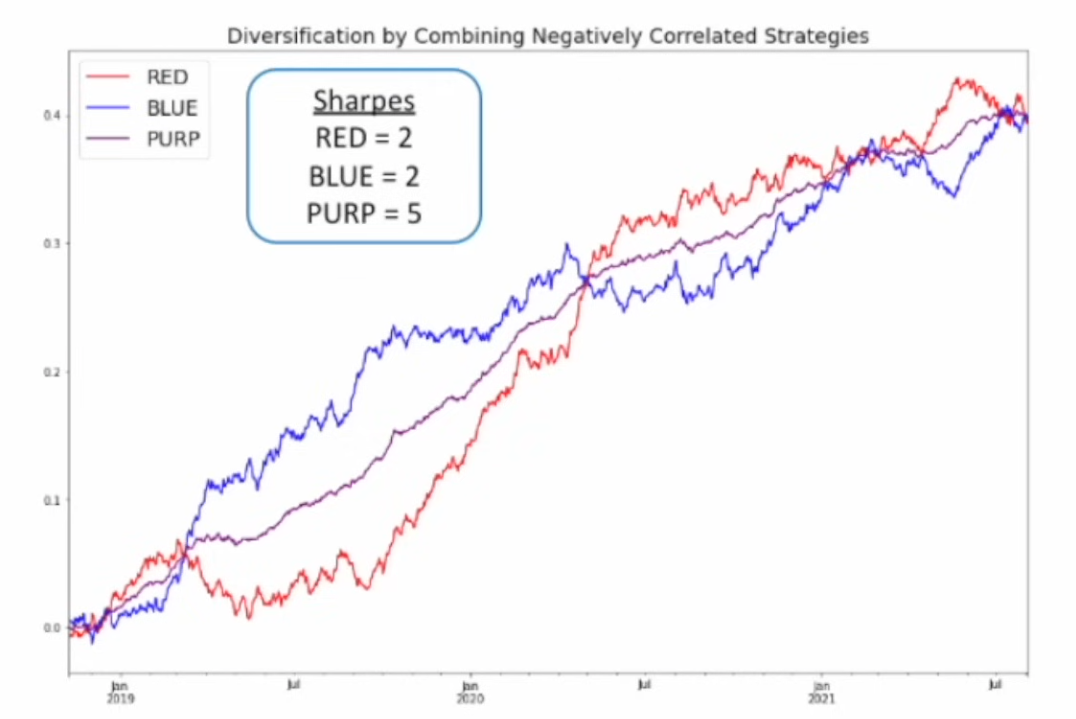
• 收益水平与持有单一资产时相近。
• 整体波动却被显著地降低了。
• 最终，该组合的夏普比率跃升至5.0。

结论：通过将具有互补性（低相关或负相关）的资产组合在一起，可以在不牺牲收益的前提下大幅降低整体风险，从而极大提升夏普比率。这是现代投资组合理论的核心。夏普比率正是衡量这种“1+1>2”协同效应的标尺，而单纯的收益率对此完全无能为力。

七、常见问题：高夏普比低收益，还有用吗？

一个常见的疑问是：如果一个策略夏普很高但绝对收益低，而另一个收益高但夏普低，是否意味着夏普比率不实用？毕竟我们最终想要的是“赚更多钱”。

这里的关键在于杠杆（Leverage）的调节作用。

杠杆的作用机制
杠杆是指借入资金来放大投资规模。例如，你用100美元本金，再借入100美元，总投资额变为200美元，这就是2倍杠杆。

• 若资产上涨1%，你的回报是2%（自有资金和借贷资金各赚1%）。
• 若资产下跌1%，你的亏损也是2%。

这里有个关键点：夏普比率在使用杠杆后保持不变。 因为收益和波动率会同比放大，它们的比值不变。

这意味着，你可以通过施加杠杆，将一个高夏普比率但低绝对收益的策略，放大为高绝对收益的策略，同时不损害其优异的单位风险回报特性。

优势总结：高夏普比率的策略具备“鱼与熊掌兼得”的潜力——既保持了低波动的稳健特性，又能通过合理的杠杆运用来满足你对高绝对收益的追求。当然，杠杆本身也带来额外的风险（如爆仓、借贷成本），需要严格管理。

八、理论基础：为什么夏普比率是合理的？

1. 统计学基础
研究证明，夏普比率与统计检验中的t统计量成正比。t统计量用于检验一个策略的平均收益是否显著大于零。因此，更高的夏普比率直接意味着更高的统计显著性，表明正收益更可能源于策略的有效性而非运气。

2. 金融学基础：现代投资组合理论（MPT）
在由哈里·马科维茨和威廉·夏普（夏普比率提出者）奠基的现代投资组合理论框架下：

• 理性投资者均追求“高收益、低风险”（以波动率衡量）。
• 理论推导出，所有投资者都应持有同一个最优风险资产组合——即切点组合（Tangency Portfolio）。
• 而这个切点组合，正是所有可能组合中夏普比率最高的那一个。

因此，最大化夏普比率不仅是经验之谈，更是理论上的最优解。

九、总结与启示

1. 收益与风险不可分割：夏普比率提供了将二者统一考量的客观标尺，避免陷入“唯收益率论”的陷阱。
2. 超越单资产比较：它是评估投资组合分散化与对冲效果的关键指标，能揭示资产间的协同效应。
3. 高夏普策略具备可扩展性：即使初始绝对收益不高，也可通过杠杆放大，同时在风险调整后收益维度保持领先。
4. 确立现实目标：长期持续实现夏普比率大于2.0，是穿越市场周期、稳健获利的卓越标志。