该论文主要探讨了如何利用 T-KAN 改进高频交易(HFT)中限价订单簿(LOB)的预测能力。
一、摘要
高频交易环境下的限价订单簿(LOB)数据具有极大的噪声和非线性。传统模型(如 DeepLOB)面临 Alpha衰减(Alpha Decay) 的挑战,即随着预测时间范围(k)的增加,预测能力迅速下降。本文提出了 T-KAN 模型,利用可学习的 B样条(B-spline)激活函数 替代标准 LSTM 中固定的线性权重。这使得模型能够学习市场信号的“形状”而非仅仅是幅度。
主要成果:
- 在 FI-2010 数据集上,预测范围
k=100 时,F1-Score 相对提升了 19.1%。
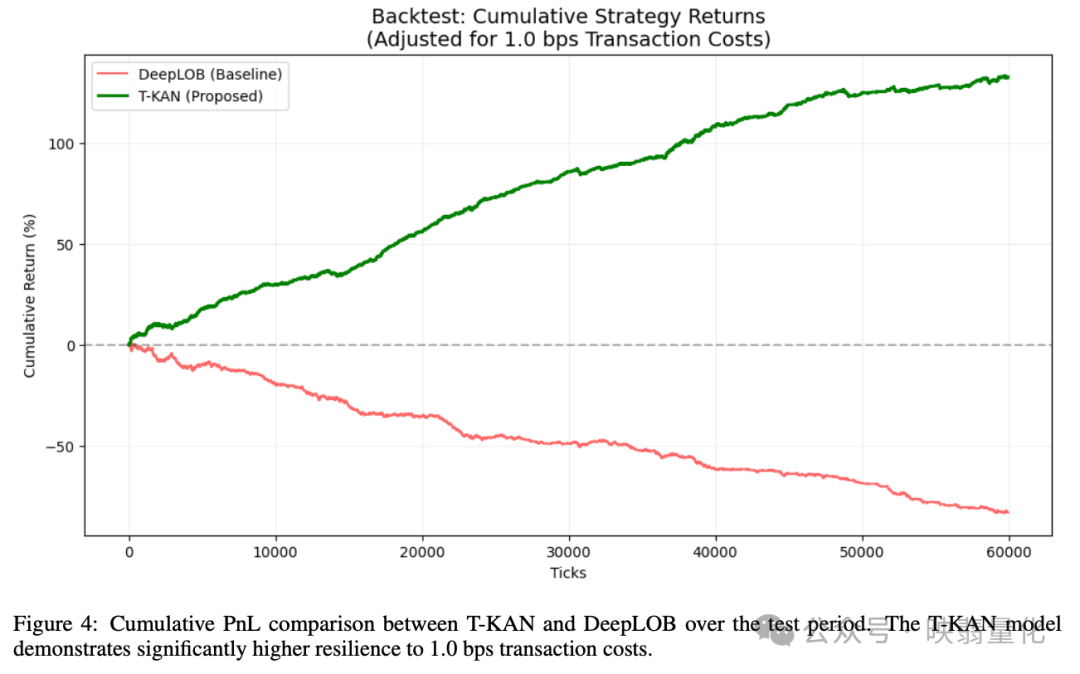
- 在考虑 1.0 bps 交易成本的模拟回测中,T-KAN 实现了 132.48% 的回报率,而 DeepLOB 则亏损 -82.76%。
该模型还具有良好的可解释性(能观察到样条函数中的“死区”以过滤噪声),且适合通过高层次综合(HLS)在 FPGA 上实现低延迟部署。
二、引言
- LOB 特性:LOB 是一个高维、离散事件的动态系统。研究聚焦于“竞价阶段(Auction Phase)”,该阶段价格发现剧烈,存在结构性流动性转移。
- 建模需求:模型需要能够捕捉复杂的、具有“路径依赖”特征的非线性关系。
- 传统方法的局限:标准 LSTM 依赖于固定的点状激活函数(如 Sigmoid/Tanh)和静态权重矩阵(
W),这种“通用逼近”方法在处理微观结构数据的局部震荡时参数效率低下。
- T-KAN 方案:通过用可学习的单变量样条函数替换静态矩阵,T-KAN 允许“在边缘上进行计算(computation on the edges)”,从而提供高分辨率的流形来捕捉激进的价格发现过程。
三、文献综述
3.1 市场微观结构中的深度学习:
- FI-2010 是基准数据集。
- 发展历程:从 CNN(提取空间特征)到 DeepLOB(CNN+LSTM 处理时空依赖)再到 TABL(注意力机制)。
- 问题:由于“维数灾难”,固定激活函数的网络在建模高频分量时受限。
3.2 Kolmogorov-Arnold Networks (KAN) 与样条理论:
- 基于 Kolmogorov-Arnold 表示定理,多元连续函数可以表示为单变量连续函数的和。
- KAN 将这些函数参数化为 B样条(B-splines)。通过可学习的样条,网络学习激活函数本身,从而更精细地拟合非线性 LOB 流形。
3.3 循环机制与 T-KAN 混合体:
- 缺陷:普通 KAN 缺乏内部记忆状态,不擅长捕捉时间序列的顺序依赖(即“时间缺口”)。
- 解决方案:T-KAN (KAN-LSTM) 混合架构。在 T-KAN 单元中,利用 KAN 层重新定义 LSTM 的门控逻辑(输入门、遗忘门、输出门)。
- 公式变化:将线性变换转变为基于样条的函数变换。
- 损失函数:为解决类别不平衡(中性类别占 65%),采用了 逆频率加权(Inverse Frequency Weighting) 的多类交叉熵损失函数。

四、方法论
4.1 数据框架:
- 使用 FI-2010 基准数据集 ,特征经过 Z-score 标准化。
- 滑动窗口单元:使用
T=10 的回溯视窗构建输入样本 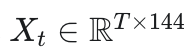 ,以捕捉订单流的动量。 ,以捕捉订单流的动量。
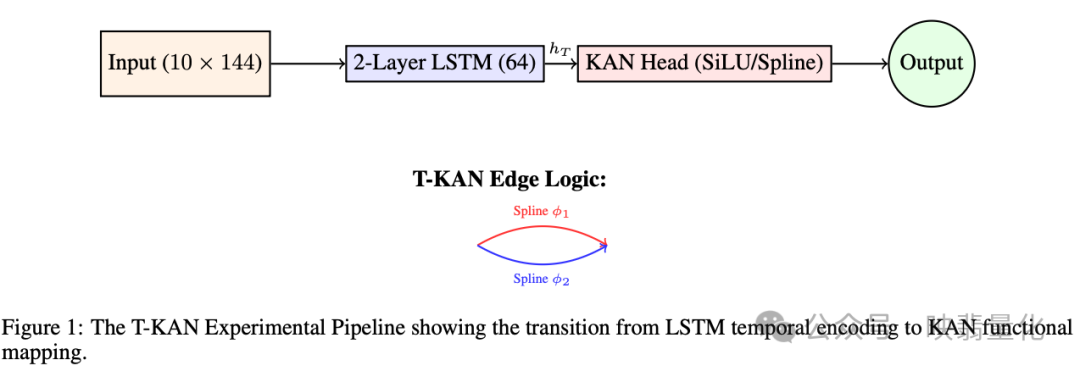
4.2 架构规范:
- DeepLOB 基线:CNN 提取特征 + LSTM 处理时序。
- T-KAN 配置:
- 使用双层 LSTM 编码器(64个隐藏单元)捕捉高频依赖。
- 最终隐藏状态输入到一个 KAN 优化分类头(KAN Head) 。
- 该结构能将潜在表示投影到高维流形上,有效划分波动的竞价阶段数据。
4.4 优化与权重:
- 逆频率加权损失 解决类别不平衡
- 使用 L1 稀疏惩罚
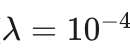 确保样条曲线的平滑性。 确保样条曲线的平滑性。
五、实验结果
测试条件:预测范围 k=100 ticks(测试对信息衰减的鲁棒性)。
5.1 性能对比指标:
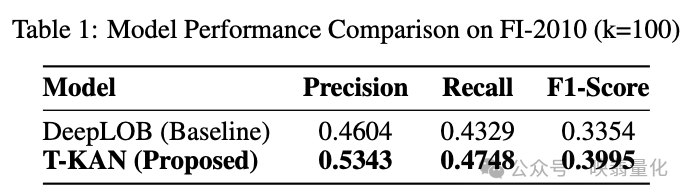
- T-KAN 在所有主要分类指标上均显著优于 DeepLOB。
- F1-Score:T-KAN (0.3995) vs DeepLOB (0.3354),提升 19.1%。
- Precision (精确率):T-KAN (0.5343) 更高,表明其在识别趋势反转和减少假阳性信号方面能力更强。
5.2 模型可解释性:
- T-KAN 学习到的激活函数呈现非线性的 S型曲线(S-curve)。
- 该曲线在零均值输入附近有效地创建了一个 “死区(dead-zone)” ,能够过滤微观结构的噪声,同时非线性地放大高置信度的信号。
5.3 经交易成本调整的回测:
- 设置 1.0 bps 的交易成本进行中间价交易模拟。
- DeepLOB:无法克服执行摩擦,最终回报 -82.76%。
- T-KAN:最终回报 132.48%。
结论:T-KAN 具有更高的“单位参数盈利密度”,证明了增加参数量(10.4万 vs 5.8万)的经济合理性。
六、结论
实验验证了使用 Kolmogorov-Arnold 层比标准线性变换更能从高频 LOB 数据中提取 Alpha。
6.1 经济可行性:T-KAN 不仅统计准确率高,更能识别出在扣除市场费用后依然盈利的高置信度流动性失衡。
6.2 对 Alpha 衰减的鲁棒性:随着预测视野 k 的增加,T-KAN 保持了比 CNN 基线更高的“Alpha 持久性”(信息系数 IC 下降较慢)。
6.3 行业展望与 FPGA 实现:
- 可解释性:能够自动过滤“买卖价差跳动(bid-ask bounce)”噪音。
- 硬件加速:KAN 层依赖于局部的 B样条评估,而非密集的矩阵乘法,非常适合 FPGA 的 高层次综合(HLS) ,有望实现亚微秒级的推理速度,满足顶级做市商和 HFT 的需求。
论文与资源:
本文探讨的T-KAN模型,结合了深度学习中的循环网络与可解释的样条函数,为使用Python处理高频金融数据预测提供了新思路,其核心的B样条优化与自定义损失函数设计值得深入分析。对量化交易与算法模型感兴趣的朋友,欢迎在云栈社区交流探讨。 |