趋势跟踪作为一种经典的系统化交易策略,在历史上于多个资产类别中均表现优异,尤其是在市场出现极端行情的年份。
然而,传统的趋势跟踪策略在构建投资组合时,往往采用“波动率倒数”加权,这种方法被称为波动率平价(Volatility Parity)。它隐含地假设资产间相关性为零。当资产间的相关性结构变得复杂时,这种朴素的风险配置方法就会失效,导致组合的实际风险暴露与预期严重偏离。
本文将探讨如何将风险平价(Risk Parity)——特别是扩展到多空框架下的扩展风险平价——引入趋势跟踪策略,以系统性地解决相关性结构变化带来的风险集中问题。
数学定义
设 t 时刻投资组合中包含 N 个风险资产。
- 收益率向量:R_t = (R_1,t, …, R_N,t)^T
- 协方差矩阵:Σ_t
- 权重向量:w_t = (w_1,t, …, w_N,t)^T
- 组合波动率:σ_p,t = √(w_t^T Σ_t w_t)
定义 1: 资产 i 的边际风险贡献定义为组合波动率对该资产权重的偏导数:
MRC_i,t = ∂σ_p,t / ∂w_i,t = (Σ_t w_t)_i / σ_p,t
定义 2: 资产 i 对组合的总风险贡献定义为权重乘以边际风险贡献:
TRC_i,t = w_i,t · MRC_i,t = w_i,t (Σ_t w_t)_i / σ_p,t
根据欧拉定理关于齐次函数的性质,组合的总波动率等于各资产总风险贡献之和:
σp,t = ∑(i=1)^N TRC_i,t
经典趋势跟踪与波动率平价
传统的趋势跟踪策略通常包含两个核心步骤:信号生成与组合构建。
信号生成
假设回顾窗口为 M 个月,t 时刻资产 i 的趋势信号 s_i,t 通常定义为过去收益率的符号:
si,t = sign( ∑(k=1)^M R_i,t-k )
波动率平价加权
为了使不同波动率的资产在组合中具有可比的影响力,传统方法采用波动率倒数加权。我们称之为波动率平价。
在 t 时刻,资产 i 的权重 w_i,t 构建如下(忽略杠杆常数):
w_i,t^(VP) ∝ s_i,t / σ_i,t
这种构建方式的核心假设是:通过赋予高波动资产较低的权重,所有资产将为组合贡献相同的风险。这与动态规划等优化思想中的朴素加权有相似之处,都忽略了要素间的相互影响。
波动率平价的理论缺陷
虽然波动率平价试图通过倒数加权来均衡风险,但是在资产间存在相关性时,VP 实际上会导致风险配置的严重失衡。
定理 1:(波动率平价的风险贡献非均衡性)若资产间存在非零相关性,则各资产的实际总风险贡献 TRC_i,t 一般不相等,即波动率平价无法实现风险平价。
证明: 由定义可知,资产 i 的总风险贡献为:
TRC_i,t^(VP) = w_i,t^(VP) (Σ_t w_t^(VP))_i / σ_p,t
展开协方差项 (Σ_t w_t^(VP))_i 并代入波动率平价权重 w_j,t^(VP) = s_j,t / σ_j,t(其中 c 为归一化常数):
(Σ_t w_t^(VP))i = ∑(j=1)^N σ_i,t σ_j,t ρ_ij,t · (s_j,t / σ_j,t) = s_i,t σ_i,t + σi,t ∑(j≠i) s_j,t ρ_ij,t
化简中间项,σ_j,t 与 1/σ_j,t 被抵消:
TRC_i,t^(VP) ∝ (s_i,t / σ_i,t) · [ s_i,t σ_i,t + σi,t ∑(j≠i) s_j,t ρ_ij,t ] / σ_p,t
注意到 s_i,t^2 = 1 且 s_i,t s_j,t = sign(s_i,t s_j,t),我们将上式分解为自身方差贡献和相关性贡献:
TRCi,t^(VP) ∝ [1 + ∑(j≠i) sign(s_i,t s_j,t) ρ_ij,t ] / σ_p,t
风险平价要求 TRC_i,t^(VP) = TRC_j,t^(VP) 对所有 i, j 成立,这等价于要求
∑_(j≠i) sign(s_i,t s_j,t) ρ_ij,t = constant(对所有 i)
然而,这一条件仅在以下特殊情形下成立:
- 所有资产两两相关性为零,ρ_ij,t = 0
- 相关性结构恰好满足某种对称性(在实际市场中极为罕见)
根据上述推导结果 TRCi,t^(VP) ∝ 1 + ∑(j≠i) sign(s_i,t s_j,t) ρ_ij,t,所以 VP 策略下的风险贡献并非恒定,而是正比于该资产与投资组合的平均相关性。
当某一类资产内部高度同质化,或者宏观因子主导市场时,ρ_ij,t 趋向于 1。此时,VP 依然按照历史波动率分配权重,未对高相关性进行惩罚。组合在实际上大幅超配了那些“抱团”波动的资产,这完全背离了“平价”的初衷。
因此,在相关性不稳定的真实市场中,我们需要一种能够内生化相关性结构的配置方法——即真正的风险平价。
风险平价的优化视角
为了解决 VP 的缺陷,我们需要直接针对 TRC_i,t 进行优化。相关研究表明,风险平价问题可以转化为一个凸优化问题。
多头风险平价
定理 2:(多头风险平价的凸优化形式)考虑以下优化问题(假设仅做多,即 w_i ≥ 0):
maxw ∑(i=1)^N ln(w_i)
s.t. w^T Σ_t w = σ_target^2, w_i ≥ 0
该优化问题的最优解 w_t^(RP) 满足风险平价性质,即所有资产的风险贡献 TRC_i,t 相等。
证明:构建拉格朗日函数 L(w, λ) = ∑ ln(w_i) - λ (w^T Σ_t w - σ_target^2)。
对 w_i 求一阶最优性条件:
∂L/∂w_i = 1/w_i - 2λ (Σ_t w)_i = 0
即:
(Σ_t w)_i = 1/(2λ w_i)
这意味着所有资产的 (Σ_t w)_i 均与 1/w_i 成比例,因此所有 w_i (Σ_t w)_i(即 TRC_i)均等于同一个常数,实现了风险平价。
扩展风险平价
传统的风险平价仅讨论 w_i ≥ 0 的情况,因为 ln(w_i) 在负数域无定义。然而,趋势跟踪策略本质上是多空策略。当趋势信号 s_i,t 为负时,我们需要持有空头头寸。
为了将风险平价引入趋势跟踪,我们需要构建扩展风险平价框架。我们的目标是:
- 权重的符号 sign(w_i,t) 必须与趋势信号 s_i,t 一致。
- 在考虑相关性的前提下,每个资产的风险贡献 TRC_i,t 相等(或与某种“得分”成比例)。
定理 3:(多空信号的扩展风险平价) 设 s_t 为给定的趋势信号向量。定义扩展的优化问题如下:
maxw ∑(i=1)^N ln(|w_i|)
s.t. w^T Σ_t w = σ_target^2
sign(w_i) = sign(s_i,t)
该问题的最优解 w_t^(ERP) 满足 TRC_i,t = TRC_j,t,即实现了多空环境下的风险平价。
证明:进行变量代换,令 u_i = |w_i|,则 w_i = s_i,t u_i。 由于约束 sign(w_i) = sign(s_i,t),我们有 u_i ≥ 0。 此时,组合的方差可以表示为:
w^T Σ_t w = u^T (S_t Σ_t S_t) u = u^T \tilde{Σ}_t u
其中 S_t = diag(s_t),\tilde{Σ}_t 是调整符号后的协方差矩阵。 优化问题转化为关于 u 的标准形式:
max_u ∑ ln(u_i)
s.t. u^T \tilde{Σ}_t u = σ_target^2, u_i ≥ 0
构建拉格朗日函数并求导,过程同定理2,可得最优解满足 u_i (\tilde{Σ}_t u)_i = constant。
利用链式法则映射回原始空间,注意到
TRC_i = w_i (Σ_t w)_i = s_i,t u_i · (Σ_t S_t u)_i = u_i (S_t Σ_t S_t u)_i = u_i (\tilde{Σ}_t u)_i
代入得 TRC_i = constant,证毕。
对比小结
通过上述推导,我们可以深刻理解两种策略在数学结构上的本质区别。
-
波动率平价 的权重是显式解析解:
w_i^(VP) ∝ s_i,t / σ_i,t
它仅依赖于自身的波动率 σ_i,t,完全切断了与其他资产的联系。
-
风险平价 的权重是隐式解: 由 TRC_i = w_i (Σ_t w)_i = constant,可得:
w_i^(RP) ∝ 1 / (Σ_t w)_i
当资产 i 与其他资产高度正相关((Σ_t w)_i 很大)时,为了维持等式,RP 优化器自动降低 w_i。这种自动惩罚高相关性的机制是其核心优势,其背后的数学原理可以在基础科学板块找到更多基础支撑。
RP vs VP 实证分析
我们构建了一个纯商品期货的实证环境。 投资范围包含黑色、有色、能化、农产品、贵金属等板块的中国商品期货。
参数设置:
- 信号回顾窗口:M = 12 个月。
- 波动率/协方差估计窗口:L = 60 天。
- 目标波动率:σ_target = 15%。
实证结果表明,在长期维度上,RP:TF(风险平价趋势跟踪)显著跑赢了 VP:TF(波动率平价趋势跟踪)。
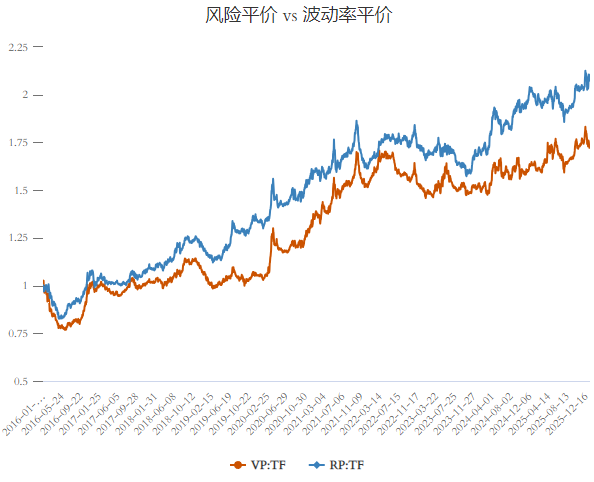
为了直观展示两种策略的本质区别,我们考察不同板块在组合中的风险贡献占比。
在 VP 策略中,权重仅由 1/σ_i,t 决定。当某一板块内部各品种相关性急剧上升时,虽然各品种的波动率可能变化不大,但组合在该板块的实际风险暴露会成倍增加。
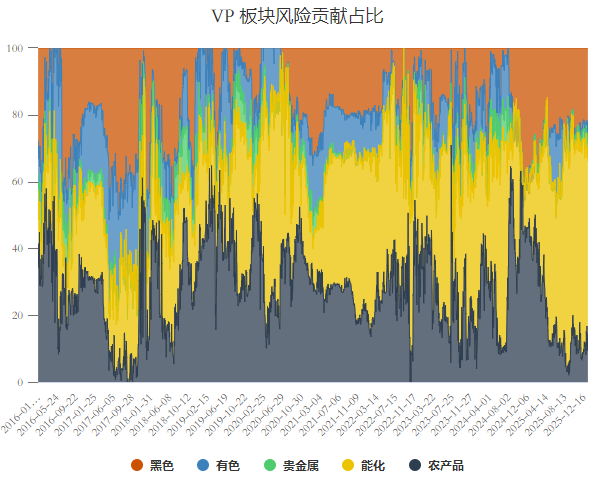
图中各颜色区域(代表不同板块)的宽度随时间剧烈波动,说明 VP 策略无法稳定控制各板块的风险暴露。
在 RP 策略中,优化目标强制约束了 TRC_i。 当板块内部相关性上升时,优化器为了保持 TRC_i 恒定,会自动削减该板块的名义权重。无论市场相关性如何变化,各板块对总组合的风险贡献始终保持相对稳定。
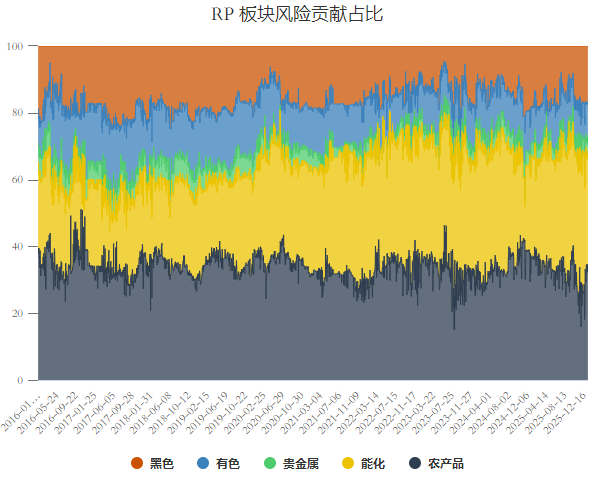
扩展风险平价与信号强度
在定理 3 中,我们展示了如何通过最大化对数效用函数来实现风险平价。然而,在实际的量化投资中,我们往往对不同资产的趋势信号有不同程度的“确信度”。
例如,一个平稳上涨的趋势可能比一个剧烈波动的趋势更值得分配风险预算。为此,我们引入广义扩展风险平价。
基于信号强度的风险分配
定理 4:(基于信号强度的风险预算) 设 b_i,t = α_i,t · s_i,t 为资产的信号强度,其中 α_i,t ≥ 0 代表我们希望分配给资产 i 的相对风险预算,s_i,t 代表持仓方向。考虑以下优化问题:
maxw ∑(i=1)^N α_i,t ln(|w_i|)
s.t. w^T Σ_t w = σ_target^2
sign(w_i) = sign(s_i,t)
该问题的最优解 w_t^ 满足:
TRC_i,t ∝ α_i,t
即:每个资产的风险贡献(TRC)与其信号强度的绝对值成正比。
证明:令 u_i = |w_i|,目标函数变为 ∑ α_i,t ln(u_i)。 构建拉格朗日函数:L = ∑ α_i,t ln(u_i) - λ (u^T \tilde{Σ}_t u - σ_target^2)。
一阶条件:
∂L/∂u_i = α_i,t / u_i - 2λ (\tilde{Σ}_t u)_i = 0
整理得:
u_i (\tilde{Σ}_t u)_i = α_i,t / (2λ)
映射回原始权重空间,注意到 TRC_i = u_i (\tilde{Σ}_t u)_i,因此:
TRC_i ∝ α_i,t,证毕。
趋势信号强度
我们这里定义几种基于趋势形态的信号强度 α_i,t。
- 基础风险平价:这是最基础的风险平价,假设所有趋势方向明确的资产应承担相同的风险。α_i,t = 1。
- 回归斜率:使用价格序列回归斜率的 t 统计量。 |t-stat| 值越大,趋势越显著且噪音越小,给予更高的风险预算。α_i,t ∝ |t-stat|。
- 夏普比率: 单位波动率带来的动量越强,配置的风险预算越高。α_i,t ∝ |Return/Vol|。
- 低波资产倾斜: 这是一个特殊的变体。它倾向于给低波动资产分配更多的风险预算。α_i,t ∝ 1/Vol。
不同的信号强度,代表了对趋势信号不同的利用方式。 我们回测结果如下:
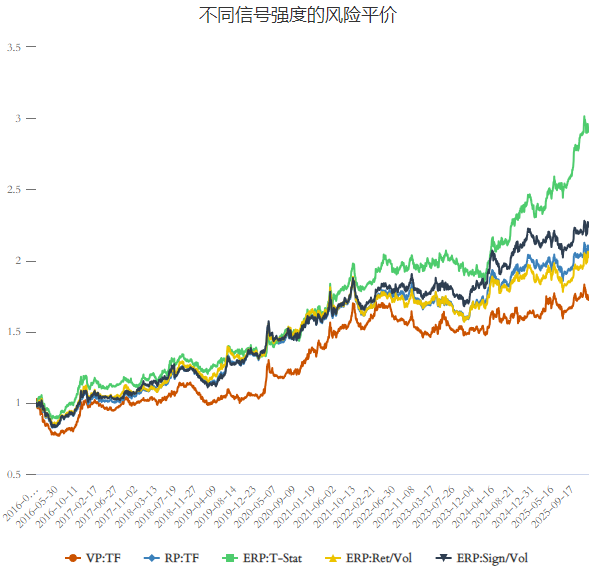
总结
本文通过理论推导与实证,详细阐述了将趋势跟踪策略的构建核心从“资产配置”转向“风险配置”的必要性。
- 我们证明了波动率平价是风险平价在零相关假设下的特例。在真实的高相关性市场环境中,VP 会导致风险向高相关资产组聚集。
- 通过引入对数效用函数的凸优化框架,我们不仅解决了多空环境下的风险平价求解问题,还实现了将信号强度与风险预算的结合。这类优化思想在量化策略的精细化调整中具有广泛应用。
- 基于中国商品期货市场的回测显示,RP 策略通过动态调整相关性结构变化带来的风险暴露,能够更稳定地控制组合风险,进而潜在地提升长期风险调整后收益。
希望这篇关于风险平价在趋势跟踪中应用的深入探讨,能为你在量化策略开发的路上带来新的启发。欢迎在云栈社区与我们继续交流更多量化交易与算法优化的心得。