Python实现Tensor视图：内存共享机制与数据依赖深度解析

本文将深入探讨在Python环境中实现的Tensor视图系统中的核心机制：内存共享与数据依赖分析。通过剖析Tensor、TensorView和Operation三个核心组件的设计与实现，我们将详细阐述视图间数据依赖产生的必要条件——共享底层存储与内存区域重叠。文章不仅提供了完整的代码实现，包括内存重叠检测算法与依赖分析逻辑，还引入了数学公式来描述视图映射关系，并通过多个具体示例展示不同场景下的数据依赖模式。

1. Tensor与TensorView的基本结构

1.1 Tensor类实现

Tensor类是基础的数据容器，负责管理实际的内存分配和数据存储。它包含数据形状、数据类型等元数据，以及实际的数据缓冲区。每个Tensor实例都拥有独立的内存管理能力，为后续的视图创建提供基础。Tensor本身不直接参与计算操作，而是作为数据的底层存储。

import numpy as np
from typing import Tuple, List, Optional, Dict, Any

class Tensor:
    def __init__(self, name: str, shape: Tuple[int, ...], dtype: str = "float32"):
        self.name = name
        self.shape = shape
        self.dtype = dtype
        self.data = np.zeros(shape, dtype=dtype)

    @property
    def size(self) -> int:
        return np.prod(self.shape)

    def get_storage_size(self) -> int:
        return self.data.size

成员	描述
name	张量名称标识
shape	张量维度形状
dtype	数据类型定义
data	实际数据存储
size	元素总数属性
get_storage_size	获取存储空间大小

1.2 TensorView类实现

TensorView是Tensor的轻量级视图，它通过引用共享Tensor的内存而不拥有实际存储。视图包含offset和stride参数，这两个参数共同定义了从视图索引到底层存储索引的映射关系。

这里有一个关键的设计原则：数据流依赖于TensorView而不是Tensor。这意味着计算操作通过TensorView间接访问Tensor的存储，而不是直接操作Tensor。这种设计实现了数据访问与计算逻辑的解耦，使得多个操作可以安全地并发访问同一Tensor的不同区域。TensorView提供了数据访问的抽象层，使得操作可以以不同的方式解释同一块内存，而Tensor则专注于存储管理。

class TensorView:
    def __init__(self, name: str, tensor: Tensor, offset: int = 0,
                 shape: Optional[Tuple[int, ...]] = None,
                 stride: Optional[Tuple[int, ...]] = None):
        self.name = name
        self.tensor = tensor
        self.offset = offset

        if shape is None:
            self.shape = tensor.shape
        else:
            self.shape = shape

        if stride is None:
            self.stride = self._compute_default_stride()
        else:
            self.stride = stride

    def _compute_default_stride(self) -> Tuple[int, ...]:
        strides = []
        stride_product = 1
        for dim in reversed(self.shape):
            strides.insert(0, stride_product)
            stride_product *= dim
        return tuple(strides)

    def get_physical_index(self, indices: Tuple[int, ...]) -> int:
        physical_idx = self.offset
        for i, idx in enumerate(indices):
            physical_idx += idx * self.stride[i]
        return physical_idx

重要方法原理说明：

1. _compute_default_stride方法：

   • 用途：计算默认的行优先步长。
   • 原理：从最后一个维度开始，步长乘积初始为1，然后向前累积每个维度的尺寸。
   • 数学表示：对于k维形状(s₀, s₁, ..., sₖ₋₁)，默认步长为(s₁×...×sₖ₋₁, ..., sₖ₋₁, 1)。
   • 示例：形状(3, 4, 5)的默认步长为(20, 5, 1)。

2. get_physical_index方法：

   • 用途：将视图索引转换为底层存储的物理索引。
   • 原理：使用公式 offset + Σ(stride[i] × index[i]) 计算。
   • 重要性：这是TensorView与底层存储之间的关键映射关系。

成员	描述
name	视图名称标识
tensor	底层张量引用
offset	视图起始偏移量
shape	视图形状定义
stride	视图步长参数
_compute_default_stride	计算默认步长方法
get_physical_index	获取物理索引方法

1.3 视图映射的数学描述

视图索引到物理存储索引的映射关系可以用数学公式精确表示。对于一个k维视图，其索引 (i₀, i₁, ..., iₖ₋₁) 映射到物理索引 p 的公式为：

p = offset + Σ_{j=0}^{k-1} stride[j] × i_j

其中：

• offset 是视图在底层存储中的起始位置。
• stride[j] 是第j维的步长。
• i_j 是第j维的索引，满足 0 ≤ i_j < shape[j]。

对于连续存储的默认步长，有：
stride[j] = Π_{m=j+1}^{k-1} shape[m]

2. 操作（Operation）的定义与执行

2.1 Operation基类

Operation基类抽象了计算操作的基本接口。每个操作都有输入视图列表和输出视图列表，这些视图可以指向相同或不同的Tensor。操作的输入和输出通过TensorView来指定，而不是直接操作Tensor。

一个重要概念：数据流可以通过两种方式形成

1. 显式数据流：一个操作的输出视图直接作为另一个操作的输入视图。
2. 隐式数据流：两个操作使用同一个Tensor的不同视图，且这些视图在内存上有重叠，通过内存重叠形成的数据依赖。

隐式数据流是TensorView系统的关键特性：一个操作的输出视图不必成为另一个操作的输入视图，数据流可以通过同一个Tensor上的内存重叠关系形成。当一个操作的输出视图与另一个操作的输入视图在内存上有重叠时，第二个操作实际上读取了第一个操作写入的部分内容，从而形成了数据依赖。

class Operation:
    def __init__(self, name: str):
        self.name = name
        self.input_views: List[TensorView] = []
        self.output_views: List[TensorView] = []

    def set_inputs(self, *views: TensorView) -> 'Operation':
        self.input_views.extend(views)
        return self

    def set_outputs(self, *views: TensorView) -> 'Operation':
        self.output_views.extend(views)
        return self

    def execute(self) -> None:
        raise NotImplementedError

重要方法原理说明：

1. set_inputs和set_outputs方法：
   • 用途：设置操作的输入输出视图。
   • 原理：使用链式调用模式，允许流畅的API设计。
   • 重要性：这些方法定义了操作的数据接口，是构建计算图的基础。

成员	描述
name	操作名称标识
input_views	输入视图列表
output_views	输出视图列表
set_inputs	设置输入视图方法
set_outputs	设置输出视图方法
execute	执行操作逻辑方法

2.2 具体操作实现

class FillOperation(Operation):
    def __init__(self, name: str, fill_value: float = 1.0):
        super().__init__(name)
        self.fill_value = fill_value

    def execute(self) -> None:
        pass

class TransformOperation(Operation):
    def __init__(self, name: str):
        super().__init__(name)

    def execute(self) -> None:
        pass

class ReduceOperation(Operation):
    def __init__(self, name: str, axis: int = -1):
        super().__init__(name)
        self.axis = axis

    def execute(self) -> None:
        pass

class BinaryOperation(Operation):
    def __init__(self, name: str):
        super().__init__(name)

    def execute(self) -> None:
        pass

重要方法原理说明：

1. FillOperation.execute方法：

   • 用途：填充输出视图的所有元素为指定值。
   • 原理：遍历输出视图的所有位置，设置对应物理存储位置的值。
   • 重要性：这是数据初始化的基础操作。

2. TransformOperation.execute方法：

   • 用途：对输入视图进行变换，结果写入输出视图。
   • 原理：从输入视图读取数据，应用变换函数，写入输出视图。
   • 重要性：支持各种数据变换操作。

操作类	描述
FillOperation	填充操作，将输出视图填充为指定值
TransformOperation	变换操作，对输入视图进行变换
ReduceOperation	规约操作，沿指定轴进行规约
BinaryOperation	二元操作，对两个输入视图进行计算

3. 简单示例：单操作多视图

3.1 示例结构与数据流

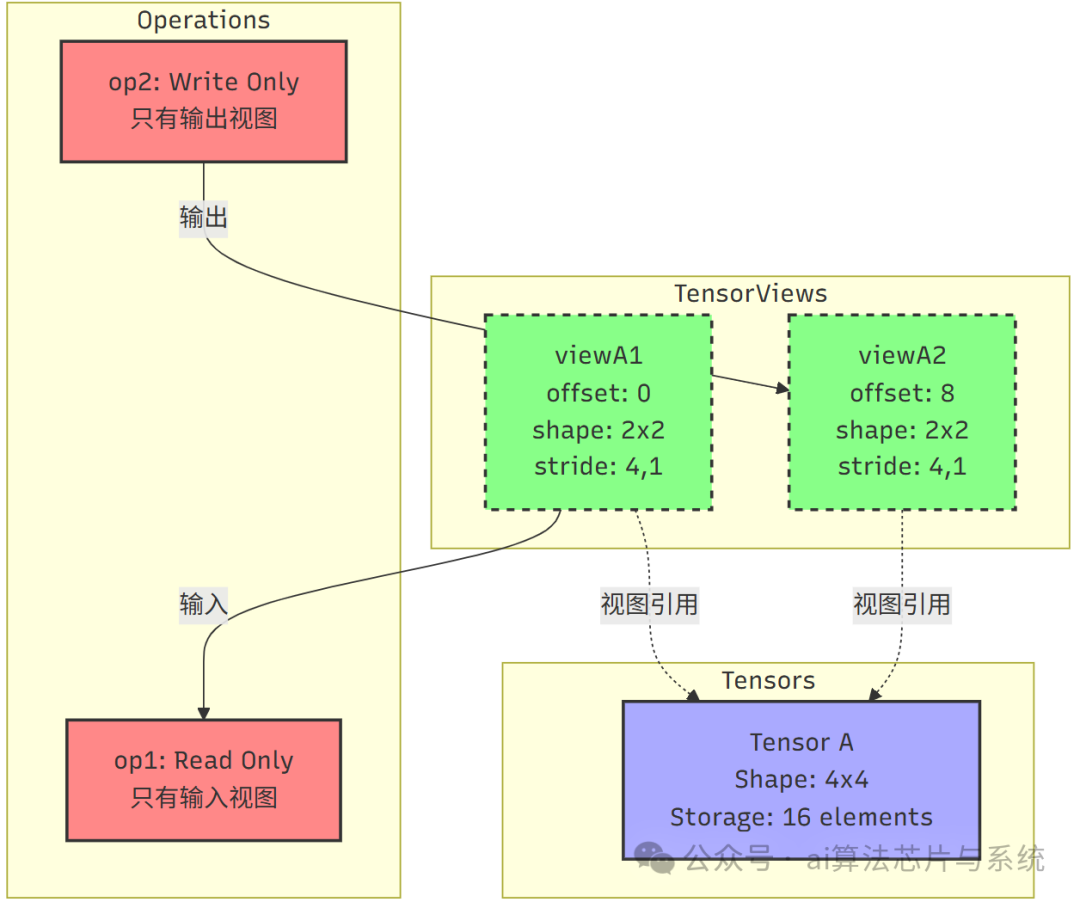
这个简单示例展示了一个Tensor被两个视图共享的情况，以及两个操作分别使用这些视图。该示例展示了以下关键特性：

1. 单一操作的输入视图：op1只使用输入视图viewA1，没有输出视图。
2. 单一操作的输出视图：op2只使用输出视图viewA2，没有输入视图。
3. 视图共享：两个视图都指向同一个Tensor A，但没有直接的数据流关系。
4. 没有数据依赖：由于两个操作使用的视图区域没有重叠，它们可以并行执行。

这个示例展示了TensorView系统的基本使用模式：操作通过视图访问数据，但操作之间不一定需要形成显式的数据流。

3.2 代码实现

下面的代码展示了TensorView的基本使用模式：操作可以只使用输入视图（如op1，纯读取），也可以只使用输出视图（如op2，纯写入）。这种灵活性允许我们构建各种类型的计算模式。

def create_simple_example() -> Dict[str, Any]:
    """创建简单示例：单一操作的多视图使用"""
    tensor_a = Tensor(name="Tensor_A", shape=(4, 4))

    # 创建两个不重叠的视图
    view_a1 = TensorView(
        name="viewA1",
        tensor=tensor_a,
        offset=0,
        shape=(2, 2),
        stride=(4, 1)
    )

    view_a2 = TensorView(
        name="viewA2",
        tensor=tensor_a,
        offset=8,  # 从第2行第0列开始 (2*4 + 0 = 8)
        shape=(2, 2),
        stride=(4, 1)
    )

    # 创建只使用输入视图的操作（读取操作）
    op1 = TransformOperation(name="read_op")
    op1.set_inputs(view_a1)  # 只有输入，没有输出

    # 创建只使用输出视图的操作（写入操作）
    op2 = FillOperation(name="write_op", fill_value=2.0)
    op2.set_outputs(view_a2)  # 只有输出，没有输入

    return {
        "tensor": tensor_a,
        "views": [view_a1, view_a2],
        "operations": [op1, op2]
    }

示例说明：

1. 视图布局：

   • viewA1覆盖元素：[0, 1, 4, 5]
   • viewA2覆盖元素：[8, 9, 12, 13]
   • 两个视图没有重叠区域。

2. 操作特性：

   • op1是纯读取操作，只使用输入视图viewA1。
   • op2是纯写入操作，只使用输出视图viewA2。
   • 两个操作可以并行执行，没有数据依赖。

3. 设计意义：

   • 展示了操作可以独立地使用Tensor的视图。
   • 说明了数据流不是必须的，操作可以独立执行。
   • 为理解更复杂的依赖关系提供了基础。

这个简单示例为理解更复杂的计算图提供了基础。它展示了TensorView系统的基本概念：操作通过视图访问数据，但操作之间不一定需要形成数据流。只有当操作之间有内存重叠时，才会产生数据依赖。

4. 复杂计算图示例

4.1 示例结构与数据流

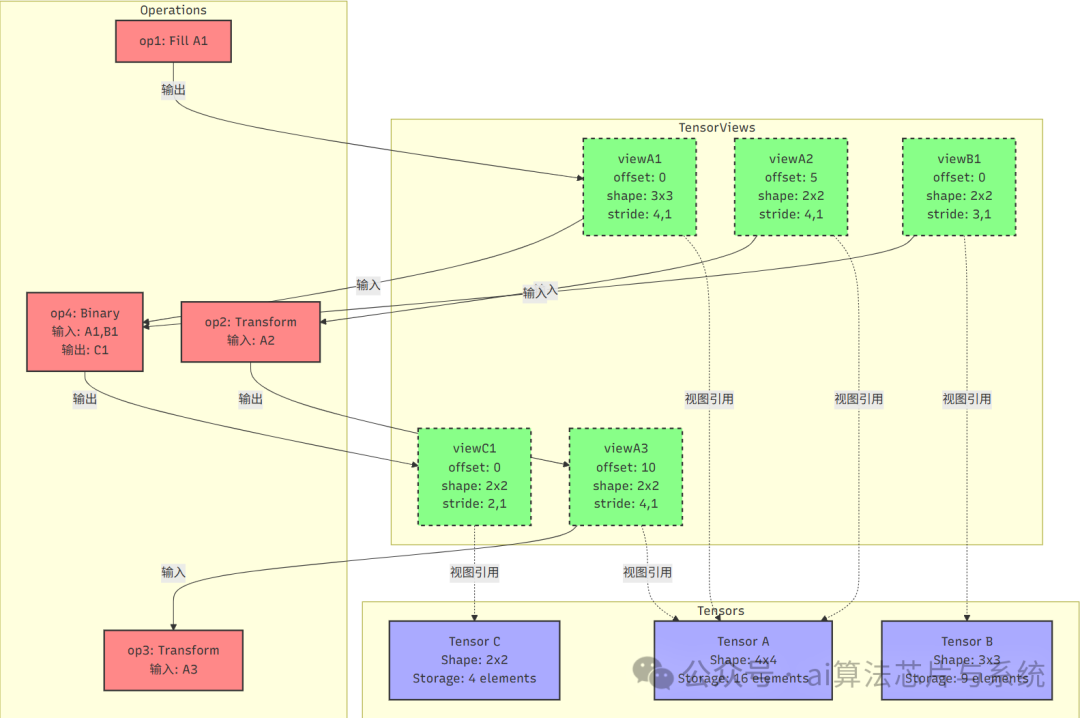
这个示例展示了更复杂的计算图结构，包含多个Tensor、多个TensorView和多个Operation。它展示了以下关键特性：

1. 隐式数据流：op1的输出viewA1和op2的输入viewA2在Tensor A的内存区域上有重叠，从而形成了隐式的数据依赖。
2. 显式数据流：op2的输出viewA3直接作为op3的输入，形成了显式的数据流。
3. 多输入操作的依赖：op4有两个输入：viewA1（来自Tensor A）和viewB1（来自Tensor B）。
4. 同一个Tensor的多个视图：Tensor A有三个不同的视图被不同操作使用。
5. 跨Tensor操作：op4的输出是viewC1，指向Tensor C。

特别强调：在这个示例中，op1的输出viewA1没有直接连接到任何操作的输入，但它与op2的输入viewA2在内存上有重叠，因此op2会读取到op1写入的内容，形成了隐式数据流。这种通过内存重叠形成的数据依赖是TensorView系统的重要特性。

4.2 代码实现

这个复杂示例展示了TensorView系统的高级特性，包括隐式和显式数据流的混合。

def create_complex_example() -> Dict[str, Any]:
    """创建复杂计算图示例，展示隐式和显式数据流"""
    tensor_a = Tensor(name="Tensor_A", shape=(4, 4))
    tensor_b = Tensor(name="Tensor_B", shape=(3, 3))
    tensor_c = Tensor(name="Tensor_C", shape=(2, 2))

    # Tensor A的视图 - 设计重叠区域
    # viewA1: 从(0,0)开始，3x3的子矩阵
    view_a1 = TensorView(
        name="viewA1",
        tensor=tensor_a,
        offset=0,
        shape=(3, 3),
        stride=(4, 1)  # 行步长4，列步长1
    )

    # viewA2: 从(1,1)开始，2x2的子矩阵，与viewA1在右下角重叠
    view_a2 = TensorView(
        name="viewA2",
        tensor=tensor_a,
        offset=5,  # 第1行第1列 (1*4 + 1 = 5)
        shape=(2, 2),
        stride=(4, 1)
    )

    # viewA3: 从(2,2)开始，2x2的子矩阵
    view_a3 = TensorView(
        name="viewA3",
        tensor=tensor_a,
        offset=10,  # 第2行第2列 (2*4 + 2 = 10)
        shape=(2, 2),
        stride=(4, 1)
    )

    # Tensor B的视图
    view_b1 = TensorView(
        name="viewB1",
        tensor=tensor_b,
        offset=0,
        shape=(2, 2),
        stride=(3, 1)
    )

    # Tensor C的视图
    view_c1 = TensorView(
        name="viewC1",
        tensor=tensor_c,
        offset=0,
        shape=(2, 2),
        stride=(2, 1)
    )

    # 创建操作
    op1 = FillOperation(name="fill_op_a", fill_value=1.0)
    op1.set_outputs(view_a1)  # 填充viewA1

    op2 = TransformOperation(name="transform_op_a")
    op2.set_inputs(view_a2).set_outputs(view_a3)  # 输入是viewA2，输出是viewA3

    op3 = TransformOperation(name="transform2_op_a")
    op3.set_inputs(view_a3)  # 输入是viewA3，没有输出（仅读取）

    op4 = BinaryOperation(name="add_op_ab")
    op4.set_inputs(view_a1, view_b1).set_outputs(view_c1)  # 两个输入，一个输出

    return {
        "tensors": [tensor_a, tensor_b, tensor_c],
        "views": [view_a1, view_a2, view_a3, view_b1, view_c1],
        "operations": [op1, op2, op3, op4]
    }

重要方法原理说明：

1. create_complex_example函数：
   • 用途：构建包含隐式和显式数据流的复杂计算图。
   • 原理：精心设计视图的offset和stride，使它们部分重叠但不完全相同。
   • 重要性：展示了TensorView系统的核心特性——通过内存重叠形成隐式数据流。

4.3 数据依赖分析

在这个复杂示例中，存在多种类型的数据依赖关系，理解这些关系需要扎实的算法与数据结构基础：

1. 隐式数据流（通过内存重叠）：

   • viewA1覆盖元素：[0,1,2,4,5,6,8,9,10]
   • viewA2覆盖元素：[5,6,9,10]
   • 重叠区域：[5,6,9,10]
   • op1写入viewA1，op2读取viewA2，由于内存重叠，op2会读取到op1写入的部分内容。
   • 这是典型的隐式数据流：一个操作的输出视图不必成为另一个操作的输入视图，通过内存重叠即可形成数据依赖。

2. 显式数据流：

   • op2的输出viewA3直接作为op3的输入。
   • 这是典型的显式数据流：一个操作的输出视图直接作为另一个操作的输入视图。

3. 多输入操作的依赖：

   • op4有两个输入：viewA1（来自Tensor A）和viewB1（来自Tensor B）。
   • op4的输出是viewC1，指向Tensor C。
   • op4依赖于op1（因为读取viewA1）和任何可能写入viewB1的操作。

4. 计算图的结构：

   • op1必须在op2之前执行（隐式依赖，通过内存重叠）。
   • op2必须在op3之前执行（显式依赖）。
   • op1必须在op4之前执行（显式依赖，因为op4直接读取viewA1）。
   • 最终形成部分有序的执行顺序：op1 -> (op2, op4) -> op3（其中op2和op4在满足各自输入依赖后可并行）。

数据依赖关系可以用依赖图表示：G = {(op1, op2), (op1, op4), (op2, op3)}。其中(op1, op2)是隐式依赖（通过内存重叠），(op1, op4)和(op2, op3)是显式依赖。

关键洞察：这种通过内存重叠形成的数据依赖允许更灵活的计算图构建。操作不需要显式地连接在一起，只要它们操作的视图在内存上有重叠，就会形成数据依赖。这使得系统可以支持更复杂的内存共享模式，但也增加了依赖分析的复杂性。

5. 内存重叠检测算法

5.1 内存覆盖范围计算

对于给定的TensorView，其在物理存储中的覆盖范围可以形式化地定义为：
Footprint(view) = {offset + Σ stride[i] × idx[i] | 0 ≤ idx[i] < shape[i]}

两个视图view1和view2的内存重叠条件为：
Footprint(view1) ∩ Footprint(view2) ≠ ∅

对于一维连续视图，覆盖范围可以简化为区间：
[offset, offset + Σ stride[i] × (shape[i]-1)]

下面的代码实现了内存重叠检测与依赖分析的核心算法：

def compute_view_footprint(view: TensorView) -> List[int]:
    """计算视图在物理存储中覆盖的所有索引"""
    footprint = set()

    def recursive_traverse(dim: int, current_idx: int):
        if dim == len(view.shape):
            footprint.add(current_idx)
            return

        for i in range(view.shape[dim]):
            recursive_traverse(dim + 1, current_idx + i * view.stride[dim])

    recursive_traverse(0, view.offset)
    return sorted(list(footprint))

def check_memory_overlap(view1: TensorView, view2: TensorView) -> bool:
    """检查两个视图是否有内存重叠"""
    if view1.tensor != view2.tensor:
        return False

    footprint1 = set(compute_view_footprint(view1))
    footprint2 = set(compute_view_footprint(view2))

    return len(footprint1.intersection(footprint2)) > 0

def analyze_dependencies(operations: List[Operation]) -> Dict[str, List[str]]:
    """分析操作间的数据依赖关系，包括隐式依赖（通过内存重叠）"""
    dependencies = {}

    for i, op in enumerate(operations):
        deps = []

        # 检查所有之前的操作
        for prev_op in operations[:i]:
            # 检查当前操作的输入是否依赖前驱操作的输出
            for input_view in op.input_views:
                for output_view in prev_op.output_views:
                    # 检查内存重叠
                    if check_memory_overlap(input_view, output_view):
                        deps.append(prev_op.name)
                        break

        dependencies[op.name] = deps

    return dependencies

重要方法原理说明：

1. compute_view_footprint函数：

   • 用途：递归计算视图覆盖的所有物理存储索引。
   • 原理：使用深度优先搜索遍历所有可能的索引组合。
   • 复杂性：时间复杂度为O(∏shape[i])，对于高维视图可能很高。
   • 优化方向：对于特殊步长模式（如连续存储）可以使用更高效的区间算法。

2. check_memory_overlap函数：

   • 用途：检查两个视图是否有内存重叠。
   • 原理：首先检查是否指向同一个Tensor，然后计算并检查足迹集合的交集。
   • 重要性：这是检测隐式数据依赖的关键。

3. analyze_dependencies函数：

   • 用途：分析操作序列间的数据依赖关系。
   • 原理：对于每个操作，检查其输入视图是否与之前任何操作的输出视图有内存重叠。
   • 重要性：这是构建正确执行顺序、避免数据竞争的基础。

函数	描述
compute_view_footprint	计算视图覆盖的物理索引
check_memory_overlap	检查两个视图是否有内存重叠
analyze_dependencies	分析操作间的数据依赖关系，包括隐式依赖

6. 总结

本文详细分析了在Python中实现的Tensor视图系统中的内存共享机制和数据依赖关系。通过数学公式形式化描述了视图映射关系，并通过复杂度递增的示例展示了不同场景下的数据依赖模式。

关键结论：

1. 数据流的两种形成方式：

   • 显式数据流：一个操作的输出视图直接作为另一个操作的输入视图。
   • 隐式数据流：两个操作使用同一个Tensor的不同视图，且这些视图在内存上有重叠，通过内存重叠形成数据依赖。

2. 隐式数据流的重要性：

   • 一个操作的输出视图不必成为另一个操作的输入视图。
   • 数据流可以通过同一个Tensor上的内存重叠关系静默形成。
   • 这种设计允许更灵活的计算图构建和高效的内存共享模式，是许多高性能计算框架（如NumPy的视图操作）的基石。

3. 数据依赖的产生条件：

   • 同一Tensor内的隐式依赖：通过内存重叠产生，即 Footprint(view_out) ∩ Footprint(view_in) ≠ ∅。
   • 显式依赖：通过操作的输入输出直接连接。

4. 视图映射的数学描述：

   • 物理索引计算：p = offset + Σ stride[j] × i_j。
   • 默认步长：stride[j] = Π_{m=j+1}^{k-1} shape[m]。

5. 系统的层次结构：

   • Tensor：负责底层存储管理。
   • TensorView：提供灵活的数据访问视图，支持内存共享。
   • Operation：实现计算逻辑，通过TensorView访问数据。

6. 复杂依赖模式：

   • 隐式依赖链：通过内存重叠形成的依赖关系。
   • 显式依赖链：通过操作直接连接形成的依赖关系。
   • 混合依赖：计算图中同时包含隐式和显式依赖。

Tensor视图机制通过灵活的offset和stride参数实现了高效的内存复用和复杂的数据访问模式。隐式数据流的支持使得系统可以构建更灵活的计算图，允许多个操作共享同一块内存区域而不需要显式连接。这种设计在深度学习框架和科学计算中特别有用，可以支持原地操作、视图操作等高级特性，同时保持高效的内存使用。

组件	角色	关键特性
Tensor	数据存储	管理实际内存分配
TensorView	数据视图	提供灵活访问方式，支持内存共享和隐式数据流
Operation	计算操作	通过视图访问数据，支持显式和隐式依赖

这种三层架构实现了存储、访问和计算的分离，提供了高度的灵活性和运行效率。隐式数据流的支持是TensorView系统的核心优势之一，它使得内存共享和数据依赖的管理更加精细和高效。希望本文的探讨能帮助你更深入地理解Python生态中张量操作背后的内存管理哲学。如果你想了解更多类似的Python底层原理或与其他开发者交流，欢迎访问云栈社区进行探讨。