PyTorch Autograd机制深度剖析：从计算图到C++实现原理解析

PyTorch的自动梯度求解(Autograd)功能是该框架受欢迎的一个重要因素。开发者只需构建好前向计算图，调用backward()函数即可自动完成梯度的反向传播。然而，其官方实现源码超过千行，对初学者而言理解成本较高。因此，本文将从其最核心的基础——一维梯度运算开始，抽丝剥茧地分析其运作机制。主要内容包括：

1. 梯度计算的核心概念。
2. 如何利用计算图进行逐步梯度求解。
3. 用C++从零实现一个简易的Autograd系统。

核心概念引导

本文的“一维”特指一个仅包含维度0的向量，可视为标量（scalar）。 “梯度运算”在机器学习中频繁出现，其数学本质是利用链式法则求微分。 首先回顾两个基础问题，用以重温“前向计算”、“反向传播”与“链式求导”：

1. y = z；已知 z=1，grad_y=1，求 y 与 grad_z 的值。
2. y = 2*z；z = x^2；已知 x=2，grad_y=1，求 z， y， grad_z， grad_x 的值。

答案： 问题1：y = 1， grad_z = 1。 问题2：z = 4， y = 8， grad_z = 2， grad_x = 8（验证代码见文末附1）。 问题1与2的计算虽简单，却涵盖了完整的梯度求解流程。复杂的自动梯度计算正是这些基本单元的叠加。

一个PyTorch程序示例

import torch
x = torch.tensor([-2], dtype=torch.float32, requires_grad=True)   
z = 2 * x
y1 = z + 5
y2 = (z * z).relu() + x + 3
loss = y1 - y2 + y2 * x
loss.backward()
print(x.grad.item())                # 打印x的梯度值

该程序包含了Autograd的典型操作。请先思考：

• 若手动计算 x.grad，过程如何？结果与程序输出是否一致？
• 程序内部的梯度是如何算出的？若让你编码实现此过程，该如何入手？

一、数学求解过程

首先，明确数学求解过程。提取程序中的运算，得到如下公式：

1. z = 2 * x
2. y1 = z + 5
3. s = z * z
4. y2 = relu(s) + x + 3 (其中 relu(x) = x if x >= 0 else 0)
5. loss = y1 - y2 + y2 * x

自动微分计算原理

基本概念

假设每个值由两个部分组成 (value, grad)：

• value 表示 forward 的数值
• grad 是反向运算得到的梯度值

单步梯度计算

对于单步的梯度计算满足公式：

∇x_new = ∇x_old + (∂y/∂x) * ∇y  ...(6)

其中：

• ∇x_new - 待求参数的梯度值
• ∇x_old - 当前梯度值
• ∂y/∂x - 是正向函数 y=f(x) 的求导函数
• ∇y - 是反向传递过来的梯度值

复合函数求导

对于 f = f1 + f2 + ... + fk 的求导公式为：

∂f/∂x_i = ∂f1/∂x_i + ∂f2/∂x_i + ... + ∂fk/∂x_i  ...(7)

通过公式 7 可知，对于复杂的求导可拆成多个子式进行线性叠加。

计算流程

结合公式 6 和 7，当需要计算 x 梯度时：

1. 先找到与 x 相关的所有正向计算
2. 然后构建每个正向计算的反向公式并计算梯度分量
3. 将梯度分量进行叠加得到最终结果

运算可以依次迭代运行，也可以并发执行。

计算示例

如下图所示，当计算 x_0 的梯度时，需要按照公式 6，依次用 y_0、y_1 和 y_2 的更新梯度 x_0.grad。

计算图结构

    x_0  ──f_0(x)──> y_0
    │                 │
   grad             grad
    │                 
    ├──f_1(x)──> y_1
    │   (dy1/dx0)     │
    │               grad
    │
    x_1 ──f_2(x)──> y_2
    │                 │
   grad             grad

具体计算过程

假设条件：

y_1 = 2 * x_0 - x_1
y = (1, 3)
x = (1, 2)
∂y/∂x = 2
∇y = 3

代入公式 6 计算：

∇x_0_new = ∇x_0_old + (∂y/∂x) * ∇y
∇x_0_new = 2 + 2 * 3
∇x_0_new = 8

伪代码实现

# 前向传播
def forward(x_0, x_1):
    y_0 = f_0(x_0)
    y_1 = f_1(x_0)  # y_1 = 2 * x_0 - x_1
    y_2 = f_2(x_1)
    return y_0, y_1, y_2

# 反向传播
def backward(x_0, grad_y_0, grad_y_1, grad_y_2):
    # 初始化梯度
    grad_x_0 = 0

    # 累加来自 y_0 的梯度贡献
    grad_x_0 += (dy_0/dx_0) * grad_y_0

    # 累加来自 y_1 的梯度贡献
    grad_x_0 += (dy_1/dx_0) * grad_y_1  # dy_1/dx_0 = 2

    # y_2 不依赖 x_0，无需累加

    return grad_x_0

关键优势

求解中可以发现，计算 x_0 的梯度并不需要分析 x_1 与 y_0/y_1/y_2 之间梯度求解的关系，这样就可以将运算解耦开来。

这种解耦特性使得：

✅ 计算可以并行化 - 不同参数的梯度可以独立计算

✅ 梯度计算更加高效 - 避免了不必要的依赖分析

✅ 便于分布式训练实现 - 各节点可以独立计算各自参数的梯度

实际应用场景

在深度学习框架（如 PyTorch、TensorFlow）中的应用：

# PyTorch 示例
import torch

x_0 = torch.tensor(1.0, requires_grad=True)
x_1 = torch.tensor(2.0, requires_grad=True)

# 前向传播
y_1 = 2 * x_0 - x_1

# 反向传播
y_1.backward(torch.tensor(3.0))  # 传入 ∇y = 3

# 查看梯度
print(f"x_0.grad = {x_0.grad}")  # 输出: x_0.grad = 6.0

总结

自动微分的核心思想：

1. 前向传播 - 计算函数值
2. 反向传播 - 利用链式法则计算梯度
3. 梯度累加 - 多个路径的梯度贡献线性叠加
4. 计算解耦 - 每个参数的梯度计算相互独立

二、基于计算图的梯度更新

将公式（1）~（5）构建为计算图，如下图所示。节点包含 val（值）和 grad（梯度）。计算过程分为两步：先进行前向传播（Forward）计算所有 val，再进行反向传播（Backward）迭代更新所有 grad。

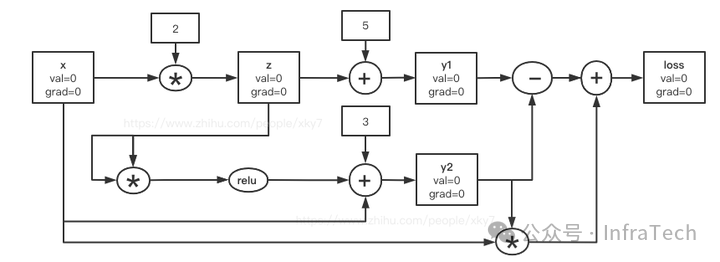
步骤1：正向求解 依序计算各节点 val： x(-2， 0) ; z(-4， 0); y1(1， 0) ; y2(17， 0) ; loss(-50， 0);

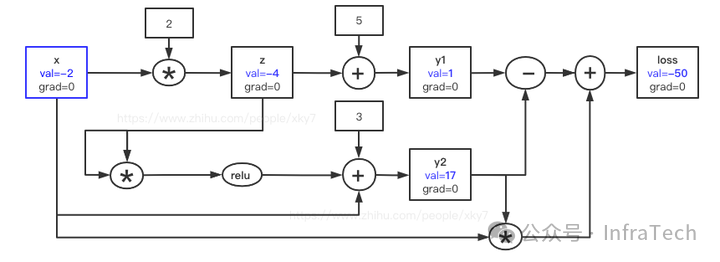
步骤2：反向求解 结合梯度公式，从 loss 节点（梯度初始为1）开始反向迭代：

• 更新 loss：loss_grad = 1，即 loss(-50, 1)。
• 更新 loss 的输入（公式5）：∂loss/∂y1 = 1， ∂loss/∂y2 = -1 + x = -3， ∂loss/∂x = y2 = 17。代入 loss_grad=1，得：
  • x.grad += 1 * 17 = 17 -> x(-5, 17)
  • y1.grad += 1 * 1 = 1 -> y1(1, 1)
  • y2.grad += 1 * (-3) = -3 -> y2(17, -3)

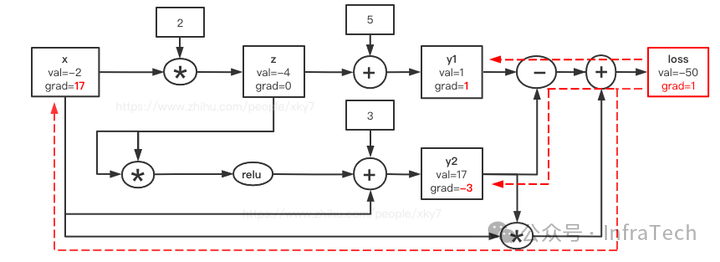
• 更新 y2 的输入（公式4）：∂y2/∂s = 1 (因为 s=16>0)， ∂y2/∂x = 1。y2_grad = -3，得：
  • s.grad += (-3) * 1 = -3 (此处 s 为中间变量，对应 z*z)
  • x.grad += (-3) * 1 = -3 -> x(-5, 14)
  • 注意 s = z * z，其梯度将传递给 z（见后续 Mul 操作）。
• *更新 s (即 zz) 的输入（乘法规则）*：`∂s/∂z = 2z = -8。s_grad = -3`，得：
  • z.grad += (-3) * (-8) = 24 -> z(-4, 24)
• 更新 y1 的输入（公式3）：∂y1/∂z = 1。y1_grad = 1，得：
  • z.grad += 1 * 1 = 1 -> z(-4, 25)

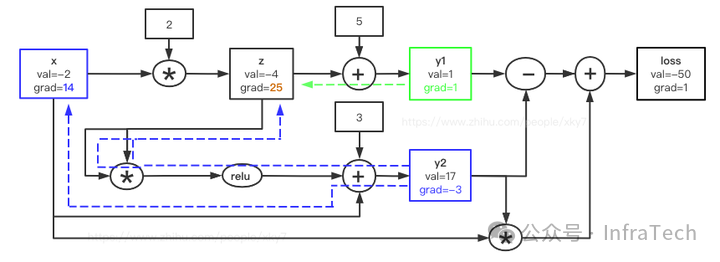
• 更新 z 的输入（公式2）：∂z/∂x = 2。z_grad = 25，得：
  • x.grad += 25 * 2 = 50 -> x(-5, 64)

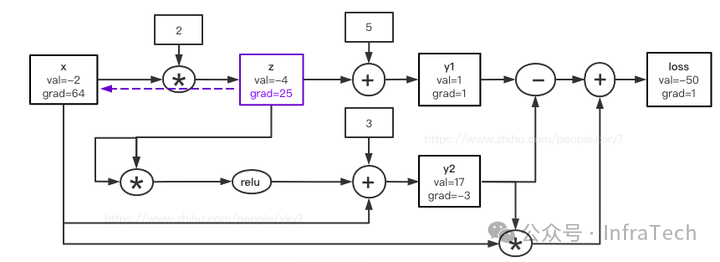
最终结果： x(-5， 64) 、 z(-4， 25)、 y1(1， 1) 、 y2(17， -3) 、 loss(-50， 1); 此结果与PyTorch程序输出完全一致，验证代码如下：

import torch
x = torch.tensor([-2], dtype=torch.float32, requires_grad=True)
z = 2 * x
y1 = z + 5
y2 = (z * z).relu() + x + 3
loss = y1 - y2 + y2 * x

# 保存中间梯度
z.retain_grad()
y1.retain_grad()
y2.retain_grad()
loss.backward()

print(f“x: {x.item()} x.grad: {x.grad.item()}“)
print(f“z: {z.item()} z.grad: {z.grad.item()}“)
print(f“y1: {y1.item()} y1.grad: {y1.grad.item()}“)
print(f“y2: {y2.item()} y2.grad: {y2.grad.item()}“)
“””
输出：
x: -2.0 x.grad: 64.0
z: -4.0 z.grad: 25.0
y1: 1.0 y1.grad: 1.0
y2: 17.0 y2.grad: -3.0
“””

计算图清晰地展示了过程，但要让程序实现，需解决两个关键问题：记住前向运算的公式、获取反向传播的拓扑顺序。

三、C++实现一个简易Autograd

一个简易的训练框架通常包含三个要素：数据（Tensor）、运算（Ops）、计算图（Graph）。 1. Tensor设计 Tensor需存储数值（val）、梯度（grad），并记录反向传播函数及上下游节点关系。

class Tensor : public enable_shared_from_this<Tensor> {
public:
  double val;                          // 存储value值
  double grad;                         // 存储梯度
  void (Tensor::*_backwardFunc)();     // 记录反向运算的函数指针
  shared_ptr<vector<TensorPtr>> cache; // 记录节点的输入依赖
  // ... 构造函数及其他成员函数
};

2. Ops定义与计算图构建 在每个运算（如加法）中，不仅计算输出值，还需注册反向函数和输入依赖。

TensorPtr operator+(TensorPtr tensorA, TensorPtr tensorB) {
  shared_ptr<Tensor> out;
  out = make_shared<Tensor>();
  out->val = tensorA->val + tensorB->val;
  // 记录依赖关系，用于构建计算图
  out->cache->push_back(tensorA);
  out->cache->push_back(tensorB);
  out->_backwardFunc = &Tensor::AddBackward; // 注册反向函数
  return out;
}
// 加法对应的反向传播函数
void Tensor::AddBackward() {
  for (auto i : *cache) {
    i->grad += this->grad; // 梯度累加
  }
}

3. 拓扑排序与反向传播 核心在于通过递归遍历，获取所有节点的拓扑排序，确保反向传播时节点按依赖的逆序执行。

void BuildTopo(TensorPtr tensor, set<TensorPtr> &visited, stack<TensorPtr> &topo) {
    if (!visited.count(tensor)) {
      visited.insert(tensor);
      for (auto input : *(tensor->cache)) {
        BuildTopo(input, visited, topo);
      }
      topo.push(tensor); // 后序放入，保证子节点在前
    }
}
void Tensor::Backward() {
    set<TensorPtr> visited;
    stack<TensorPtr> topo;
    this->grad = 1.0; // 根节点梯度初始化为1
    BuildTopo(shared_from_this(), visited, topo);
    while (!topo.empty()) {
      auto tensor = topo.top();
      topo.pop();
      if (tensor->_backwardFunc) {
        ((*tensor).*(tensor->_backwardFunc))(); // 执行反向传播
      }
    }
}

4. 完整C++实现示例 以下代码实现了文章开头的PyTorch示例的完整计算流程，揭示了Autograd的底层原理。通过系统编程的方式构建基础组件，是理解复杂框架的有效途径。

#include <iostream>
#include <memory>
#include <set>
#include <stack>
#include <vector>
using namespace std;

class Tensor;
using TensorPtr = shared_ptr<Tensor>;

class Tensor : public enable_shared_from_this<Tensor> {
public:
  double val;
  double grad;
  void (Tensor::*_backwardFunc)();
  shared_ptr<vector<TensorPtr>> cache;

  Tensor(double value = 0, double gradient = 0)
      : val(value), grad(gradient), _backwardFunc(NULL),
        cache(make_shared<vector<TensorPtr>>()) {}

  void AddBackward() {
    for (auto i : *cache) {
      i->grad += grad;
    }
  }
  void SubBackward() {
    (*cache)[0]->grad += grad;
    (*cache)[1]->grad -= grad;
  }
  void MulBackward() {
    (*cache)[0]->grad += grad * (*cache)[1]->val;
    (*cache)[1]->grad += grad * (*cache)[0]->val;
  }
  void ReluBackward() { /*... 在val>0时传播梯度 ...*/ }

  TensorPtr relu() {
    shared_ptr<Tensor> out = make_shared<Tensor>();
    out->val = this->val > 0 ? this->val : 0;
    if (this->val > 0)
      out->cache->push_back(shared_from_this());
    out->_backwardFunc = &Tensor::ReluBackward;
    return out;
  }

  void BuildTopo(TensorPtr tensor, set<TensorPtr> &u_set, stack<TensorPtr> &topo) {
    if (!u_set.count(tensor)) {
      u_set.insert(tensor);
      for (auto i : *(tensor->cache)) {
        BuildTopo(i, u_set, topo);
      }
      topo.push(tensor);
    }
  }

  void Backward() {
    set<TensorPtr> u_set;
    stack<TensorPtr> topo;
    this->grad = 1;
    BuildTopo(shared_from_this(), u_set, topo);
    while (!topo.empty()) {
      auto tensor = topo.top();
      topo.pop();
      if (tensor->_backwardFunc) {
        ((*tensor).*(tensor->_backwardFunc))();
      }
    }
  }
};

// 操作符重载（部分）
TensorPtr operator+(TensorPtr tensorA, TensorPtr tensorB) { /*...*/ }
TensorPtr operator*(TensorPtr tensorA, TensorPtr tensorB) { /*...*/ }
// ... 其他操作符

int main() {
  TensorPtr x = make_shared<Tensor>(-2);
  TensorPtr z, y1, y2, loss;
  z = 2 * x;
  y1 = z + 5;
  y2 = (z * z)->relu() + x + 3;
  loss = y1 - y2 + y2 * x;
  loss->Backward();
  cout << “loss value: “ << loss->val << endl;
  cout << “x gradient: “ << x->grad << endl;
  return 0;
}

实现说明：

1. 本例仅实现了+、-、*、relu等基础操作，读者可依此模式扩展。
2. 真实的PyTorch还需处理多维张量、设备（CPU/GPU）、更高效的内存管理等复杂问题，但其Autograd核心思想与此一致。
3. 类似实现思路也适用于其他语言，如Python的知名教学项目micrograd。

总结

一维梯度运算是理解现代深度学习框架自动微分机制的基石。透彻理解从计算图构建、拓扑排序到梯度传播的完整流程后，便可在此基础上进一步探索多维张量的支持、GPU加速等高级特性，从而更深入地掌握如PyTorch这类复杂框架的内部工作原理。

附录

附1：问题2的验证代码

import torch
x = torch.tensor([2], dtype=torch.float32, requires_grad=True)
z = x ** 2
y = 2 * z
z.retain_grad()
y.backward()
print(z.grad.item()) # 输出 2
print(x.grad.item()) # 输出 8

附2：公式1~5的复合函数求导验证 （过程略，与计算图分解求解结果一致，均为 grad_x = 64）

参考

1. PyTorch官方教程-Autograd
2. micrograd项目