[Python] DeepSeek-Math-V2开源数学推理模型解析：三重自我验证架构与实战评测

在大型语言模型不断突破推理能力边界的背景下，DeepSeek带来了全新的开源数学模型DeepSeek-Math-V2。该模型通过工程化的自我验证机制，显著提升了数学推理的准确性与可靠性，并在多项顶级数学竞赛基准测试中取得了突破性成绩：在IMO 2025模拟测试中获得83.3%（金牌级） 得分，在Putnam 2024的scaled compute模式下更是达到了118/120的接近满分表现。

一、核心亮点速览

• 全面开源：提供完整的模型权重、详细技术报告与基准评测数据。
• 创新架构：引入首创的Generator → Verifier → Meta-Verifier三层自我验证架构。
• 训练革新：基于大规模、可验证的“分步证明”语料进行专项优化训练。
• 工具融合：能够集成符号计算、定理证明器等外部工具链进行协同验证。
• 评测卓越：在IMO、Putnam、CMO等多项权威数学基准上表现突出。

此次升级，DeepSeek让模型不再仅仅是“生成答案”，而是学会了像数学家一样思考：逐步推理、主动检查、及时纠错、持续优化。

二、三重自我验证架构：系统性突破

DeepSeek-Math-V2的核心创新在于，它将“自我验证”从一个简单概念，系统化地发展为一套完整的推理与训练流水线。

1. Generator（生成器）：构建解题路径

• 接收数学问题，生成初步的证明步骤或解答过程。
• 以“推理链”形式输出细粒度的逻辑推导序列。
• 具备生成多种候选路径的能力，为后续验证筛选提供基础。

2. Verifier（验证器）：逐步判定逻辑正确性

• 对生成器输出的每一步推导进行“正确 / 可疑 / 错误”的评估。
• 可以是经过判别式任务微调的同模型版本。
• 能够自动识别逻辑跳步、引理误用、计算错误等常见问题。

3. Meta-Verifier（元验证器）：审查验证过程本身

• 用于发现并纠正验证器可能存在的盲点或误判。
• 针对高难度或易错步骤，自动增强验证强度。
• 在必要时，可调用更强大的外部符号计算工具进行终极仲裁。

这套三层闭环机制，有效解决了大模型“输出流畅但逻辑漏洞多”的痛点，使得生成的推理链能够像经过同行评审的数学论文一样被逐层检验，大幅减少了“幻觉”与逻辑谬误。

三、训练流程：聚焦“可验证的过程”

DeepSeek-Math-V2的训练范式发生了根本转变，其核心是构建一个庞大的“逐步证明”数据体系，而非仅仅依赖最终答案。

1. 强化逐步推理数据

• 训练数据包含从前提、引理到推导方式的完整逻辑链条信息。
• 每一步都经过自动化或半自动化的正确性标注与验证。
• 同时使用错误示例及其修正版本进行训练，提升模型的纠错能力。

2. 训练目标迁移：从“结果对”到“过程对”

传统模型训练通常只以最终答案的正确性作为监督信号。而DeepSeek-Math-V2的训练目标是让模型掌握：如何检查自身的推理、如何修正过程中的错误，最终形成一套可靠的解题方法论。

3. “扩展验证计算”的迭代策略

为了防止验证能力落后于不断增强的生成能力，团队采用了动态策略：

• 随着生成器能力提升，相应增加验证器的计算预算和检查深度。
• 强化元验证器的监督作用，并引入更复杂的验证工具。
• 将验证过程中发现的新模式和错误类型，回流到训练数据中，形成持续改进的数据处理闭环。

这确保了验证体系的强度始终略高于生成能力，从而让推理质量实现可持续的螺旋上升。

四、集成外部工具链：工程化数学推理

DeepSeek-Math-V2与传统LLM的一个显著区别在于，它能够主动与专业的数学工具进行协同工作：

• 自动定理证明器（如Lean、Isabelle）
• 符号计算工具（如SymPy、Mathematica引擎）
• 数值验证模块
• 定制化的外部查证脚本

当模型在推理中遇到关键或易错的步骤时，可以自动触发对这些工具的调用，利用严格的符号逻辑或数值计算来验证语言推理的结果。这种“自然语言推理 + 形式化验证”相结合的工程化方法，极大地提高了模型解决高难度数学问题的稳定性和可信度。

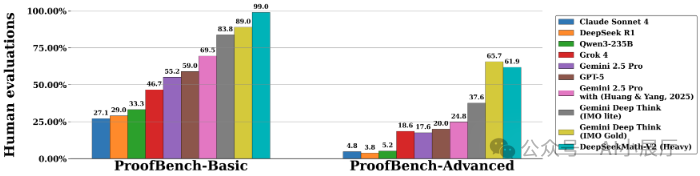
五、评测表现：多项基准领先

根据公开的评测数据，DeepSeek-Math-V2在多个高难度数学基准上展现了强大实力：

1. IMO 2025（模拟测试）

• 成功解决了6道模拟题中的5道。
• 得分率达到83.3%，达到了国际数学奥林匹克竞赛的金牌水平。

2. Putnam 2024

• 在扩展测试时间计算资源的模式下。
• 取得了118/120（98.3%） 的惊人成绩，接近满分。

3. CMO及其他竞赛基准

• 在不同难度层级的题集上，性能均显著优于同类开源模型。
• 部分测试案例显示，其推理过程具有良好的可解释性和逻辑稳定性。

这些评测结果表明，DeepSeek-Math-V2的优势不仅在于更高的“解题正确率”，更在于其“推理过程的可验证性”以及应对“高难度题目时的稳定性”。

六、开源资源：获取与复现

DeepSeek已完全公开了该模型的相关资源，方便社区研究与应用：

• 模型权重：可直接下载用于推理或进一步微调。
• 模型卡（Model Card）：包含详细的模型信息、训练数据说明和伦理考量。
• 评测脚本与数据：提供了复现论文中基准测试结果的工具。
• 技术细节：公布了验证器与元验证器的核心实现思路。
• 许可证：采用宽松的Apache 2.0开源协议。

开发者与研究人员可以从Hugging Face或GitHub平台直接获取所有资源，并依据文档复现实验结果。 模型地址：https://huggingface.co/deepseek-ai/DeepSeek-Math-V2